数学|可能函数的总数

在本文中，我们将讨论如何从一个集合到另一个集合中查找函数数。要了解函数的基本知识，可以参考以下内容： 函数类（内射、满射、双射） .

从一组到另一组的函数数： 设n和Y分别有两个元素集。在从X到Y的函数中，X的每个元素都必须映射到Y的一个元素。因此，X的每个元素都有n个元素可供选择。因此，函数总数将为n×n×n。。m次=n ^M . 例如： X={a，b，c}和Y={4，5}。从X到Y的函数可以在图1中表示。

考虑到将X元素映射到Y元素的所有可能性，函数集可以在表1中表示。

例如： 让我们在此基础上讨论登机门问题：

• 问题1。设X，Y，Z分别为X，Y和Z的大小集。设W=X×Y。设E是W的所有子集的集合。从Z到E的函数数为： （A） z ^2xy （B） z x 2 ^xy （C） z ^2x+y （D） 二, ^xyz

  解决方案： 当W=xy给定时，W中的元素数为xy。由于E是W的所有子集的集合，E中的元素数为2 ^xy .从Z（Z元素集）到E（2元素集）的函数数 ^xy 元素）是2 ^xyz .所以正确的选择是（D）

• 问题2。 设S表示所有函数的集合f:{0,1} ^4. → {0,1}. 用N表示从S到集合{0,1}的函数数。Log2Log2N的值为。 （A） 十二 （B） 十三 （C） 15 （D） 十六

  解决方案：如问题中所给出的，S表示所有函数f的集合：{0，1} ^4. → {0, 1}. 来自{0,1}的函数数 ^4. （16个元素）到{0，1}（2个元素）是2 ¹⁶ 因此，S有2个 ¹⁶ 元素。同时，给定N表示S（2）中函数的个数 ¹⁶ 元素）到{0,1}（2个元素）。因此，N有2 ²¹⁶ 元素。计算所需值，

  Log2（Log2（2 ²¹⁶ ))=Log2 ¹⁶ = 16

  因此，选项D是正确的。

从一个集合到另一个集合的函数数—— 在从X到Y的函数中，必须使用Y的所有元素。在从X={a，b，c}到Y={4，5}的函数示例中，表1中给出的F1和F2不在表1中。在F1中，集合Y的元素5未使用，而元素4在函数F2中未使用。所以，从X到Y的to函数总数是6（F3到F8）。

• 如果X有m个元素，Y有2个元素，则ON函数的数量将为2 ^M -2.

  说明： 从一组m元素到一组2元素，函数的总数是2 ^M .在这些函数中，有2个函数未映射到（如果所有元素都映射到1） ^圣 Y元素或所有元素都映射到2 ^钕 元素Y）。所以，函数的个数是2 ^M -2.

• 如果X有m个元素，Y有n个元素，则函数的数量为，

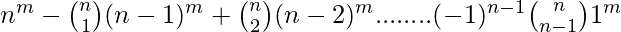
重要提示——

• 只有当m≥ n。
• 如果m

问题3。从集合X={1,2,3,4}到集合Y={a，b，c}的on函数（满射函数）的数量为： （A） 36 （B） 64 （C） 81 （D） 72

解决方案：使用m=4和n=3，ON函数的数量为： 三 ^4. – ^3. C ₁ (2) ^4. + ^3. C _2. 1. ^4. = 36.