从A到B的函数f是B的一个元素对A的每个元素的赋值(A和B是非空集)。A被称为f的域,B被称为f的共域。如果B是由函数f分配给A的元素A的B的唯一元素,它被写为f(A)=B。f将A映射到B。意味着f是从A到B的函数,它被写为 ![]()
null
与职能有关的术语:
- 域与共域 –如果f是从集合a到集合B的函数,那么a称为域,B称为共域。
- 范围 –f的范围是A元素的所有图像的集合。基本上范围是共域的子集。
- 图像和预图像 –b是a的图像,如果f(a)=b,a是b的前图像。
函数的属性:
- 加法和乘法: 设f1和f2是从A到B的两个函数,然后是f1+f2和f1。f2定义为-: f1+f2(x)=f1(x)+f2(x)。(补充) f1f2(x)=f1(x)f2(x)。(乘法)
- 平等: 只有当两个函数具有相同的域、相同的共域以及从域到共域的相同映射元素时,它们才是相等的。
功能类型:
- 一对一函数(内射): 一个函数被称为一对一,如果对于A中的所有元素A和b,如果f(A)=f(b),那么它必须是A=b的情况。它永远不会映射其函数的不同元素 领域 同一元素的 共域 .

我们可以用量词表示f是一对一的
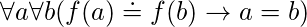 或者相当于
或者相当于 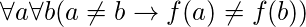 其中,话语的宇宙是功能的领域。
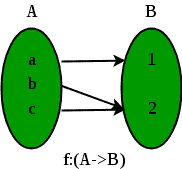
其中,话语的宇宙是功能的领域。 - 关于函数(满射): 如果b中的每个元素b在a中都有对应的元素a,使得f(a)=b,则不要求a是唯一的;f.B的一个或多个元素可以映射到A的一个或多个元素。
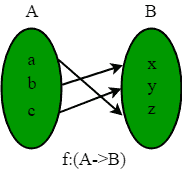
- 一对一对应函数(双射/可逆): 如果一个函数既是一对一函数又是一对上函数,那么它就是双射函数。
- 反函数: 双射函数也被称为可逆函数,因为它们具有反函数性质。双射f的逆表示为f -1 这是一个函数,它赋予b一个唯一的元素a,使得f(a)=b。因此f -1 (b) =a。
一些有用的功能-:
严格增加和严格减少功能: 当x>y时,如果f(x)>f(y),则函数f严格增加。当x
增加和减少功能: 如果f(x),函数f是递增的≥ 当x>y时为f(y)。如果f(x),函数f减小≤ f(y)当x
功能组成: 设g是从B到C的函数,f是从a到B的函数,f和g的组合,表示为fog(a)=f(g(a))。
函数组合的属性:
- 雾≠ 戈夫
- F -1 of=f -1 (f(a))=f -1 (b) =a。
- fof -1 =f(f) -1 (b) )=f(a)=b。
- 如果f和g都是一对一函数,那么fog也是一对一函数。
- 如果f和g都启动功能,则fog也启动。
- 如果f和fog都是一对一函数,那么g也是一对一。
- 如果f和fog是ON,那么g也不一定是ON。
- (雾) -1 =g -1 哦 -1
一些要点:
- 如果函数严格递增或严格递减,则为一对一。
- 一对一函数从不将相同的值分配给两个不同的域元素。
- 对于on函数,值域和余域是相等的。
- 如果函数f不是双射函数,则不能定义f的反函数。
本文由 尼蒂卡·班萨尔
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END
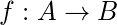


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



