抗锯齿线|吴小林算法-yiteyi-C++库

抗锯齿线图 下图显示的是用Bresenham的直线算法（左）和Wu Xiaolin的直线算法（右）绘制的直线，该算法使直线平滑。你觉得哪个更好看？ 抗锯齿概念 假设我们想要从点（1，1）到点（8，4）画一条带矩形边的线。理想的线条如图A所示。因为我想在屏幕上显示它，所以我不能使用它。生产线需要经过一个叫做 光栅化 这将决定单个像素的颜色。可以使用以下几种算法： Bresenham直线算法 , 数字微分分析仪，吴小林的直线算法，古普塔-斯普鲁尔算法。后两种方法执行抗锯齿或线条平滑。前两种算法产生的结果如图B所示。

null

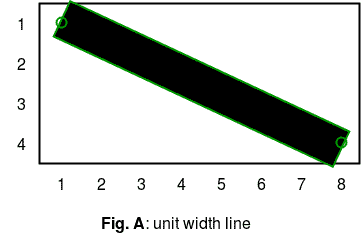
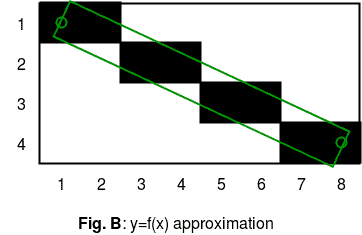
这一行几乎没有问题（图B）。 1.像素（4,2）的覆盖范围比像素（3,2）小，但它们都是全黑的。 2.像素（2,2）的覆盖范围几乎和（4,2）一样大，但它被绘制成全白色。为了克服这些缺点并产生更平滑的线条，我们使用了吴晓林的线条算法

吴晓林的直线算法 考虑下面使用BrESeNAMH线生成算法绘制的图。取一个线段及其初始坐标x。循环中的x在线段末端加1。在每一步中，都会计算误差——该位置的实际y坐标与最近的网格单元之间的距离。如果误差不超过单元高度的一半，则填充该单元。这就是整个算法。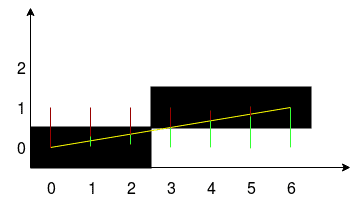我们将修改此算法，使其能够生成抗锯齿线。吴晓林的直线算法的特点是，在每一步计算中，最接近直线的两个像素都会被执行，并且根据距离的不同，它们的颜色也会不同。当前交点中间像素强度为100%如果像素在0.9像素范围内，则强度为10%。换句话说，100%的强度被分割在限制两侧矢量线的像素之间。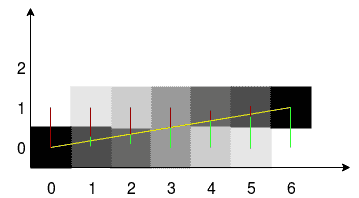在图片中，红色和绿色表示到两个相邻像素的距离。要计算误差，可以使用浮点并取小数部分的误差值。

注：以下实现使用 SDL 用于在屏幕上绘制像素的库。如果您使用的是像ubuntu这样的debian系统，只需运行以下命令即可安装SDL库。

sudo apt-get install libsdl2-dev

建造和使用

gcc filename.c -lSDL2

推荐：请尝试你的方法 {IDE} 首先，在进入解决方案之前。

注：如果线段在x轴上的投影小于在y轴上的投影，或者线段的起点和终点被交换，则该算法将不起作用。为了避免这种情况，您需要检查向量的方向及其坡度，然后交换直线的坐标，最终将所有情况简化为一种或至少两种情况。以下算法假设只有整数坐标作为输入，因为像素值不能是浮点。

                     // C program to implement Xiaolin Wu's line drawing                   
                     // algorithm.                   
                     // We must install SDL library using above steps                   
                     // to run this program                   
                     #include<SDL2/SDL.h>                   
                             
                     // SDL stuff                   
                     SDL_Window* pWindow = 0;                   
                     SDL_Renderer* pRenderer = 0;                   
                             
                     // swaps two numbers                   
                     void                               swap(                               int                               * a ,                               int                               *b)                   
                     {                   
                                         int                               temp = *a;                   
                                         *a = *b;                   
                                         *b = temp;                   
                     }                   
                             
                     // returns absolute value of number                   
                     float                               absolute(                               float                               x )                   
                     {                   
                                         if                               (x < 0)                               return                               -x;                   
                                         else                               return                               x;                   
                     }                   
                             
                     //returns integer part of a floating point number                   
                     int                               iPartOfNumber(                               float                               x)                   
                     {                   
                                         return                               (                               int                               )x;                   
                     }                   
                             
                     //rounds off a number                   
                     int                               roundNumber(                               float                               x)                   
                     {                   
                                         return                               iPartOfNumber(x + 0.5) ;                   
                     }                   
                             
                     //returns fractional part of a number                   
                     float                               fPartOfNumber(                               float                               x)                   
                     {                   
                                         if                               (x>0)                               return                               x - iPartOfNumber(x);                   
                                         else                               return                               x - (iPartOfNumber(x)+1);                   
                             
                     }                   
                             
                     //returns 1 - fractional part of number                   
                     float                               rfPartOfNumber(                               float                               x)                   
                     {                   
                                         return                               1 - fPartOfNumber(x);                   
                     }                   
                             
                     // draws a pixel on screen of given brightness                   
                     // 0<=brightness<=1. We can use your own library                   
                     // to draw on screen                   
                     void                               drawPixel(                               int                               x ,                               int                               y ,                               float                               brightness)                   
                     {                   
                                         int                               c = 255*brightness;                   
                                         SDL_SetRenderDrawColor(pRenderer, c, c, c, 255);                   
                                         SDL_RenderDrawPoint(pRenderer, x, y);                   
                     }                   
                             
                     void                               drawAALine(                               int                               x0 ,                               int                               y0 ,                               int                               x1 ,                               int                               y1)                   
                     {                   
                                         int                               steep = absolute(y1 - y0) > absolute(x1 - x0) ;                   
                             
                                         // swap the co-ordinates if slope > 1 or we                   
                                         // draw backwards                   
                                         if                               (steep)                   
                                         {                   
                                         swap(&x0 , &y0);                   
                                         swap(&x1 , &y1);                   
                                         }                   
                                         if                               (x0 > x1)                   
                                         {                   
                                         swap(&x0 ,&x1);                   
                                         swap(&y0 ,&y1);                   
                                         }                   
                             
                                         //compute the slope                   
                                         float                               dx = x1-x0;                   
                                         float                               dy = y1-y0;                   
                                         float                               gradient = dy/dx;                   
                                         if                               (dx == 0.0)                   
                                         gradient = 1;                   
                             
                                         int                               xpxl1 = x0;                   
                                         int                               xpxl2 = x1;                   
                                         float                               intersectY = y0;                   
                             
                                         // main loop                   
                                         if                               (steep)                   
                                         {                   
                                         int                               x;                   
                                         for                               (x = xpxl1 ; x <=xpxl2 ; x++)                   
                                         {                   
                                         // pixel coverage is determined by fractional                   
                                         // part of y co-ordinate                   
                                         drawPixel(iPartOfNumber(intersectY), x,                   
                                         rfPartOfNumber(intersectY));                   
                                         drawPixel(iPartOfNumber(intersectY)-1, x,                   
                                         fPartOfNumber(intersectY));                   
                                         intersectY += gradient;                   
                                         }                   
                                         }                   
                                         else                   
                                         {                   
                                         int                               x;                   
                                         for                               (x = xpxl1 ; x <=xpxl2 ; x++)                   
                                         {                   
                                         // pixel coverage is determined by fractional                   
                                         // part of y co-ordinate                   
                                         drawPixel(x, iPartOfNumber(intersectY),                   
                                         rfPartOfNumber(intersectY));                   
                                         drawPixel(x, iPartOfNumber(intersectY)-1,                   
                                         fPartOfNumber(intersectY));                   
                                         intersectY += gradient;                   
                                         }                   
                                         }                   
                             
                     }                   
                             
                     // Driver code                   
                     int                               main(                               int                               argc,                               char                               * args[])                   
                     {                   
                             
                                         SDL_Event event;                   
                             
                                         // initialize SDL                   
                                         if                               (SDL_Init(SDL_INIT_EVERYTHING) >= 0)                   
                                         {                   
                                         // if succeeded create our window                   
                                         pWindow = SDL_CreateWindow(                               "Anti-Aliased Line "                               ,                   
                                         SDL_WINDOWPOS_CENTERED, SDL_WINDOWPOS_CENTERED,                   
                                         640, 480,                   
                                         SDL_WINDOW_SHOWN);                   
                             
                                         // if the window creation succeeded create our renderer                   
                                         if                               (pWindow != 0)                   
                                         pRenderer = SDL_CreateRenderer(pWindow, -1, 0);                   
                                         }                   
                                         else                   
                                         return                               1;                               // sdl could not initialize                   
                             
                                         while                               (1)                   
                                         {                   
                                         if                               (SDL_PollEvent(&event) && event.type == SDL_QUIT)                   
                                         break                               ;                   
                             
                                         // Sets background color to white                   
                                         SDL_SetRenderDrawColor(pRenderer, 255, 255, 255, 255);                   
                                         SDL_RenderClear(pRenderer);                   
                             
                                         // draws a black AALine                   
                                         drawAALine(80 , 200 , 550, 150);                   
                             
                                         // show the window                   
                                         SDL_RenderPresent(pRenderer);                   
                                         }                   
                             
                                         // clean up SDL                   
                                         SDL_Quit();                   
                                         return                               0;                   
                     }                   

输出：

参考资料： https://courses.engr.illinois.edu/ece390/archive/archive-f2000/mp/mp4/anti.html https://unionassets.com/blog/algorithm-brezenhema-and-wu-s-line-299 https://en.wikipedia.org/wiki/Xiaolin_Wu%27s_line_algorithm 本文由 洛克什·夏尔马 .如果你喜欢GeekSforgek，并想贡献自己的力量，你也可以使用写极客。组织或者把你的文章寄去评论-team@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上，并帮助其他极客。

如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请写下评论。

文章版权归作者所有，未经允许请勿转载。

THE END

技术文章