先决条件—— 图论基础 考虑具有多个节点之间的连接的电子电路。是否可以在一块电路板上打印该电路,使所有连接都不相互交叉,即不重叠或相交? 如果我们知道 平面性 一系列的图表。
平面性—— “如果图形可以在平面上绘制,则称其为平面图形 没有任何交叉 .这样的图形称为图形的平面表示。”
重要提示—— 一个图形可能是平面的,即使它是用交叉点绘制的,因为在没有交叉点的情况下,它可能以不同的方式绘制。 例如,考虑完整的图 ![]() 以及它的两种可能的平面表示——
以及它的两种可能的平面表示—— ![图片[2]-数学|平面图与图着色-yiteyi-C++库](https://www.yiteyi.com/wp-content/uploads/geeks/geeks_planar-graph.jpg)
- 例如—— 是超立方体吗
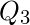 平面的?
平面的? ![图片[4]-数学|平面图与图着色-yiteyi-C++库](https://www.yiteyi.com/wp-content/uploads/geeks/geeks_hypercube.jpg)
- 解决方案—— 对
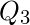 是平面的。它的平面表示-
是平面的。它的平面表示- ![图片[6]-数学|平面图与图着色-yiteyi-C++库](https://www.yiteyi.com/wp-content/uploads/geeks/geeks_hypercube-planar.jpg)
平面图中的区域——
图的平面表示法将平面拆分为 区域 。这些区域由边限定,但有一个区域是无界的。例如,考虑下面的图表 ![图片[7]-数学|平面图与图着色-yiteyi-C++库](https://www.yiteyi.com/wp-content/uploads/geeks/geeks_planar-regions.jpg) 共有6个区域,其中5个有界区域和1个无界区域
共有6个区域,其中5个有界区域和1个无界区域 ![]() . 图的所有平面表示都在相同数量的区域中分割平面。欧拉发现平面图中的区域数是图中顶点数和边数的函数。
. 图的所有平面表示都在相同数量的区域中分割平面。欧拉发现平面图中的区域数是图中顶点数和边数的函数。
定理—— “让我 ![]() 做一个 连通简单平面图 具有
做一个 连通简单平面图 具有 ![]() 边缘和
边缘和 ![]() 顶点。然后是区域的数量
顶点。然后是区域的数量 ![]() 在图中等于
在图中等于 ![]() 其中k是图中组件的数量。 .”
其中k是图中组件的数量。 .”
- 例如—— 有20个顶点且每个顶点的阶数为3的连通平面简单图中的区域数是多少?
- 解决方案—— 边缘度数之和=20*3=60。通过握手定理,
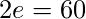 这给了
这给了 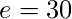 . 根据欧拉定理,区域数=
. 根据欧拉定理,区域数= 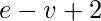 它给出了12个区域。
它给出了12个区域。
欧拉公式得到的一个重要结果是以下不等式——
注—— “如果 ![]() 是一个连通平面图
是一个连通平面图 ![]() 边缘和
边缘和 ![]() 顶点,在哪里
顶点,在哪里 ![]() 然后
然后 ![]() 而且
而且 ![]() 顶点的度数不能超过5。“
顶点的度数不能超过5。“
- 例如—— 这是图表
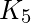 平面的?
平面的? - 解决方案—— 中的顶点和边数
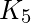 分别是5和10。因为10>3*5–6,10>9不平等
分别是5和10。因为10>3*5–6,10>9不平等 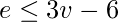 他并不满意。因此,图形不是平面的。
他并不满意。因此,图形不是平面的。
图着色-
如果你决定创建一张地图,并且需要对地图的各个部分进行最佳着色,那么你应该感到幸运,因为图论就在你身边。为地图的各个区域着色所需的最大颜色数是多少?这个问题和其他类似的问题在图论中产生了许多结果。 首先,让我们以一种形式化的方式定义着色的约束-
着色—— “简单图的着色是将一种颜色分配给图的每个顶点,使得 没有两个相邻的顶点 都被指定为相同的颜色。”
解决这个问题的一个简单方法是用不同的颜色给每个顶点上色,以得到总的颜色 ![]() 颜色。但在某些情况下,实际需要的颜色数量可能会少于此数量。
颜色。但在某些情况下,实际需要的颜色数量可能会少于此数量。
色数- “给图形上色所需的最少颜色数称为其颜色 色数 .表示为 ![]() .”
.”
对于平面图,求色数与求平面图着色所需的最小颜色数是相同的问题。
4颜色定理—— “平面图的色数不大于4。”
- 例1- 下列图的色数是多少?
![图片[28]-数学|平面图与图着色-yiteyi-C++库](https://www.yiteyi.com/wp-content/uploads/geeks/geeks_4-color-theorem.jpg)
- 解决方案—— 在图形中
 ,自顶点起,色数至少为3
,自顶点起,色数至少为3 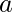 ,
, 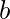 和
和 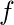 它们彼此相连。 以下颜色指定满足着色约束——
它们彼此相连。 以下颜色指定满足着色约束—— 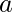 –红色
–红色 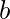 –绿色
–绿色 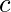 -蓝色
-蓝色 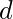 –红色
–红色 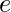 –绿色
–绿色 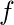 -蓝色
-蓝色 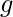 –红色 因此,色数
–红色 因此,色数  3岁。 在图形中
3岁。 在图形中 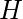 自从
自从 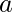 和
和 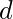 都是连通的,因此色数为4。
都是连通的,因此色数为4。
- 例2- 颜色数是多少
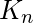 ?
? - 解决方案—— 因为在一个完整的图中,每个顶点都与其他顶点相连,所以色数是
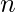 .
.
- 例3- 颜色数是多少
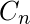 ?
? - 解决方案—— 如果顶点以交替方式着色,则循环图需要2种颜色。如果
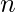 如果是奇数,那么最后一个顶点的颜色将与第一个顶点的颜色相同,因此色数将为3。但如果它是偶数,那么第一个顶点和最后一个顶点将是不同的颜色,颜色数将是2。
如果是奇数,那么最后一个顶点的颜色将与第一个顶点的颜色相同,因此色数将为3。但如果它是偶数,那么第一个顶点和最后一个顶点将是不同的颜色,颜色数将是2。
- 例4- 颜色数是多少
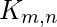 ?
? - 解决方案—— 在二部图中
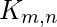 ,将中的顶点分为两组,以便同一组中的顶点之间没有边。因此,任何二部图的色数都是2。一组顶点可以指定一种颜色,另一组顶点可以指定一种不同的颜色,总共有两种颜色。它将满足着色约束,因为同一集合的顶点没有连接。
,将中的顶点分为两组,以便同一组中的顶点之间没有边。因此,任何二部图的色数都是2。一组顶点可以指定一种颜色,另一组顶点可以指定一种不同的颜色,总共有两种颜色。它将满足着色约束,因为同一集合的顶点没有连接。
关卡角问题
练习下列问题将有助于测试你的知识。所有问题都是在前几年的GATE或GATE模拟测试中提出的。强烈建议你练习。
1. 2012年CS门,问题21 2. 2011年CS门,问题17 3. 2009年CS门,问题2 4. CS门2008,问题23 5. 登机门CS 2005问题10 6. 2005年CS门,问题47 7. CS门2004,问题77 8. CS 2002号登机门,问题4 9 GATE CS 2015第1组问题63 10 C门2008,问题3 11 GATE CS 2016第2组问题13
推荐人-
平面图-维基百科 图形着色——维基百科 《离散数学及其应用》,肯尼斯·H·罗森著
本文由 希拉格·曼瓦尼 .如果你喜欢GeekSforgek,并想贡献自己的力量,你也可以使用 贡献极客。组织 或者把你的文章寄到contribute@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上,并帮助其他极客。
如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写下评论。


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



