大门|大门-CS-2005 |问题10

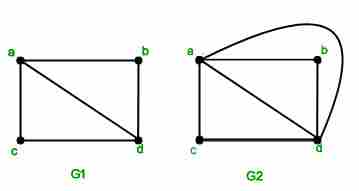
设G是一个具有13个顶点和19条边的简单连通平面图。然后，计算图的平面嵌入中的面数 （A） 6. （B） 8. （C） 9 （D） 13 答复: （B） 说明： 如果一个无向图可以在纸上绘制而不需要两条边交叉，则称其为平面图，这样的图形称为平面嵌入。我们说一个图可以嵌入平面，如果它是平面的。平面图将平面划分为区域（以边为边界），称为面。图K4是palanar图，因为它具有平面嵌入，如中所示

下图。

欧拉公式： 对于任何自身不相交的多面体（连通平面图）

•面数（F） •加上顶点数（角点）（V） •减去边数（E） ，始终等于2。这可以写成：F+V− E=2。

解决方案：

这里给出的F=？，V=13，E=19 ->F+13-19=2 ->F=8

所以答案是（B）。

这个解决方案是由 尼马尔·巴拉德瓦伊

我们可以应用欧拉公式 平面图 公式是v− e+f=2。 这个问题的小测验