先决条件—— 图论基础-集合1 图是由一组对象构成的结构,其中一些对象对在某种意义上是“相关的”。图中的对象对应于 顶点 它们之间的关系符合 边缘 .一个图形以图解的方式描述为一组点,这些点描绘的是由描绘边的线或曲线连接的顶点。 正式地
“一张图表 ![]() 包括
包括 ![]() ,一组非空的 顶点 (或节点)和
,一组非空的 顶点 (或节点)和 ![]() 一套 边缘 .每条边都有一个或两个与其关联的顶点,称为其顶点 端点 .”
一套 边缘 .每条边都有一个或两个与其关联的顶点,称为其顶点 端点 .”
图表类型: 有几种图是根据边、方向、权重等来区分的。
1.简单图- 每条边连接两条边的图形 不同的 没有两条边连接同一对顶点的顶点称为简单图。例如,考虑下面的图表——
![图片[4]-数学|图论基础-集合2-yiteyi-C++库](https://media.geeksforgeeks.org/wp-content/uploads/SIMPLE-GRAPH.jpg)
上面的图是一个简单的图,因为没有顶点有自循环,也没有两个顶点有多条边连接它们。 边由它们连接的顶点表示- ![]() 边是连接顶点的吗
边是连接顶点的吗 ![]() 和
和 ![]() .
.
2.多重图- 多条边可以连接同一对顶点的图称为多重图。 由于同一对顶点之间可能有多条边,因此 多种多样 边数表示两个顶点之间的边数。
![图片[8]-数学|图论基础-集合2-yiteyi-C++库](https://www.yiteyi.com/wp-content/uploads/geeks/geeks_hamiltonian-circuit2-2.jpg)
上面的图是一个多重图,因为它们之间有多条边 ![]() 和
和 ![]() .边缘的多样性
.边缘的多样性 ![]() 是2。
是2。
在一些图中,与上图不同的是,边是 指导的 这意味着对象之间的关系是单向的,而不是双向的。在某些应用中,边缘的方向可能很重要。
根据边缘是否有方向,我们可以 有向图 和 无向图 这个性质可以推广到简单图和多重图,得到简单有向或无向简单图和有向或无向多重图。
基本图形术语:
在上面的讨论中,已经解释了一些关于图的术语,例如顶点、边、有向边和无向边等。还有更多的术语描述顶点和边的属性。
- 邻接—— 在图表中
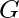 两个顶点
两个顶点 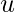 和
和 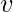 据说是 相邻 如果它们是边的端点。边缘
据说是 相邻 如果它们是边的端点。边缘 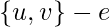 据说与顶点有关。 如果边缘是定向的,
据说与顶点有关。 如果边缘是定向的, 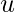 据说是毗邻
据说是毗邻 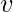 和
和 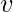 据说是邻近的
据说是邻近的 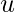 在这里
在这里 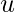 据说是 初始顶点 和
据说是 初始顶点 和 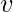 据说 终端顶点 .
据说 终端顶点 . - 学位- 顶点的阶数是与其相关联的边数,但自循环除外,它对顶点阶数的贡献是两倍。顶点度
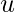 表示为
表示为 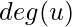 . 对于有向图,度进一步分类为 程度上 和 外学位 .顶点的阶数是以给定顶点为终点的边数。顶点的出度是以给定顶点为初始顶点的边数。在程度上表示为
. 对于有向图,度进一步分类为 程度上 和 外学位 .顶点的阶数是以给定顶点为终点的边数。顶点的出度是以给定顶点为初始顶点的边数。在程度上表示为 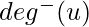 向外度表示为
向外度表示为 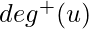 . 例如,在上面描述城市间航班的有向图中,顶点“德里”的入度为3,出度也为3。
. 例如,在上面描述城市间航班的有向图中,顶点“德里”的入度为3,出度也为3。
注: 如果顶点的度数为零,则称为 偏远的 .如果学位是1,那么就叫做 吊坠 .
握手定理:
如果把一个图的所有顶点的度数相加,会得到什么。对于无向图,每条边贡献两次,一次用于其初始顶点,另一次用于其终端顶点。所以度数之和等于边数的两倍。这一事实在握手定理中得到了说明。
Letbe an undirected graph with
edges. Then
In case G is a directed graph,
对于无向图,握手定理有一个有趣的结果——
An undirected graph has an even number of vertices of odd degree.
证据: 允许 ![]() 和
和 ![]() 分别是偶数度和奇数度的顶点集。 通过握手定理我们知道,
分别是偶数度和奇数度的顶点集。 通过握手定理我们知道, ![]() 所以
所以 ![]() 具有偶数度的顶点的度数之和为偶数。LHS也是偶数,这意味着奇数度顶点的度数之和必须是偶数。 因此,奇数阶的顶点数为偶数。
具有偶数度的顶点的度数之和为偶数。LHS也是偶数,这意味着奇数度顶点的度数之和必须是偶数。 因此,奇数阶的顶点数为偶数。
一些特殊的简单图:
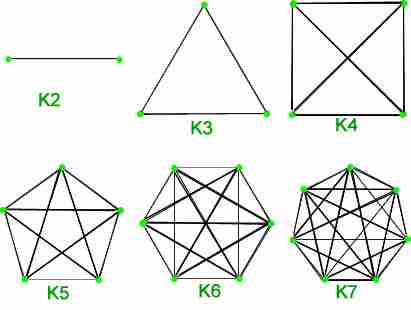
1.完整的图表- 一个简单的 ![]() 每对顶点之间只有一条边的顶点称为完整图。一个完整的
每对顶点之间只有一条边的顶点称为完整图。一个完整的 ![]() 顶点由
顶点由 ![]() .完整图中有n个顶点的边总数为n*(n-1)/2。
.完整图中有n个顶点的边总数为n*(n-1)/2。
2.周期- 圈是有顶点的简单图 ![]() 和边缘
和边缘 ![]() .骑自行车
.骑自行车 ![]() 顶点表示为
顶点表示为 ![]() .循环图中有n个顶点的边总数为n。
.循环图中有n个顶点的边总数为n。
![图片[42]-数学|图论基础-集合2-yiteyi-C++库](https://www.yiteyi.com/wp-content/uploads/geeks/geeks_cycles-300x132.jpg)
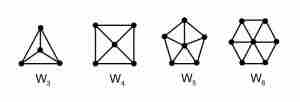
3.车轮- 一个轮子就像一个循环,有一个额外的顶点与其他每个顶点相连。车轮 ![]() 带有1个附加顶点的顶点表示为
带有1个附加顶点的顶点表示为 ![]() .轮图中有n个顶点的边总数为2*(n-1)。
.轮图中有n个顶点的边总数为2*(n-1)。
4.超立方体- 超立方体或n-立方体是一个具有 ![]() 每个顶点由一个n位字符串表示。最多相差1位的顶点由边连接。超立方体
每个顶点由一个n位字符串表示。最多相差1位的顶点由边连接。超立方体 ![]() 顶点由
顶点由 ![]() .总边数为n*
.总边数为n* ![]() 具有
具有 ![]() 立方体图中的顶点。
立方体图中的顶点。
![图片[51]-数学|图论基础-集合2-yiteyi-C++库](https://www.yiteyi.com/wp-content/uploads/geeks/geeks_hypercube-2.jpg)
5.二部图- 简单的图形 ![]() 如果其顶点集
如果其顶点集 ![]() 可以划分为两个不相交的集合,以便
可以划分为两个不相交的集合,以便 ![]() 其初始顶点位于第一个集合中,终点顶点位于第二个集合中。二部图中有(n+m)个顶点的边的总数为(n*m)。
其初始顶点位于第一个集合中,终点顶点位于第二个集合中。二部图中有(n+m)个顶点的边的总数为(n*m)。
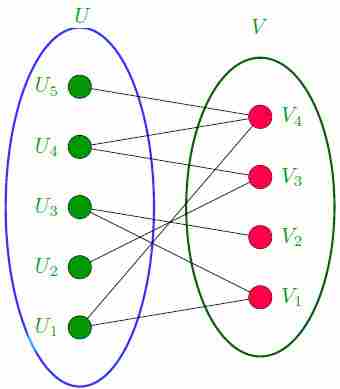
定理—— 一个简单的图是二部的当且仅当可以指定两个图中的一个时 图的每个顶点都有不同的颜色,这样就不会为相邻的两个顶点指定颜色 同样的颜色。
一个带参数的二部图 ![]() 和
和 ![]() 如果从第一个集合中的每个顶点到第二个集合中的每个顶点都有一条边,总共有
如果从第一个集合中的每个顶点到第二个集合中的每个顶点都有一条边,总共有 ![]() 边缘。A. 完全二部图 具有
边缘。A. 完全二部图 具有 ![]() 第一个集合中的顶点和
第一个集合中的顶点和 ![]() 第二组中的顶点表示为
第二组中的顶点表示为 ![]() .
.
![图片[62]-数学|图论基础-集合2-yiteyi-C++库](https://www.yiteyi.com/wp-content/uploads/geeks/geeks_complete-graphs-bipartite.jpg)
关卡角问题
练习下列问题将有助于测试你的知识。所有问题都是在前几年的GATE或GATE模拟测试中提出的。强烈建议你练习。
1. 2013年CS门,问题25 2. GATE CS 2014第1组问题61 3. 2006年CS门,问题71 4. CS 2002号登机门,问题25 5. CS门2004,问题37 6. GATE CS 2014第2组问题13
推荐人-
图表——维基百科 《离散数学及其应用》,肯尼斯·H·罗森著
本文由 希拉格·曼瓦尼 .如果你喜欢GeekSforgek,并想贡献自己的力量,你也可以使用 写极客。组织 或者把你的文章寄去评论-team@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上,并帮助其他极客。
如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写下评论。



![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



