求三角形外心的程序-yiteyi-C++库

给定二维平面P、Q和R中的3个非共线点及其各自的x和y坐标，求出三角形的外心。注：三角形的外心是由三角形的三个顶点构成的圆的中心。请注意，三个点可以唯一地确定一个圆。例如：

null

Input : P(6, 0)        Q(0, 0)        R(0, 8)Output : The circumcenter of the triangle PQR          is: (3, 4)Input : P(1, 1)        Q(0, 0)        R(2, 2)Output : The two perpendicular bisectors found          come parallel. Thus, the given points          do not form a triangle and are collinear

推荐：请尝试你的方法 {IDE} 首先，在进入解决方案之前。

给定三角形的三个点，我们可以很容易地找到三角形的边。现在，我们有了三角形三条边的直线方程。在得到这些之后，我们可以通过一个简单的属性来找到三角形的外心，如下所示：

三角形的外心是三角形边的所有垂直平分线相交的点。

下图对此进行了很好的解释。

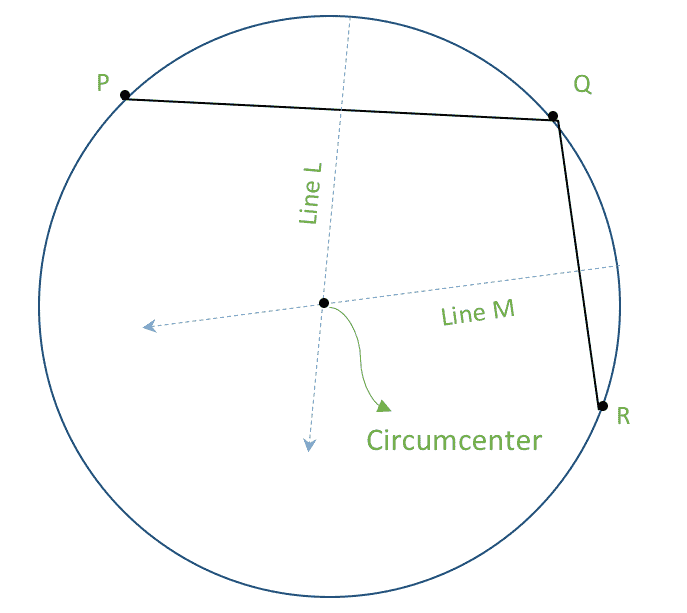
Circumcenter of a Triangle

请注意，不需要找到三角形的所有三条边。找到两条边就足够了，因为我们只需要使用两条垂直平分线就可以唯一地找到交点。第三条垂直平分线将自身穿过所找到的外心。要做的事情可以分为以下几部分：

找出两条线（比如PQ和QR），它们构成三角形的边。
找到PQ和QR的垂直平分线（分别是线L和线M）。
求L和M线的交点作为给定三角形的外心。

第一步 参考这篇文章通过程序查找通过2个点的线 第二步 让PQ表示为ax+by=c 对于某些d，垂直于该线的线表示为-bx+ay=d。然而，我们对垂直平分线感兴趣。我们找到P和Q的中点，把这个值放到标准方程中，我们得到d的值。同样，我们对QR重复这个过程。

d = -bx + aywhere, x = (x_p + x_q)/2AND y = (y_p + y_q)/2

第三步 参考这篇文章两条直线的交点程序

CPP

                         // C++ program to find the CIRCUMCENTER of a                       
                         // triangle                       
                         #include <iostream>                       
                         #include <cfloat>                       
                         using                                     namespace                                     std;                       
           
                         // This pair is used to store the X and Y                       
                         // coordinate of a point respectively                       
                         #define pdd pair<double, double>                       
           
                         // Function to find the line given two points                       
                         void                                     lineFromPoints(pdd P, pdd Q,                                     double                                     &a,                       
                                                 double                                     &b,                                     double                                     &c)                       
                         {                       
                                                 a = Q.second - P.second;                       
                                                 b = P.first - Q.first;                       
                                                 c = a*(P.first)+ b*(P.second);                       
                         }                       
           
                         // Function which converts the input line to its                       
                         // perpendicular bisector. It also inputs the points                       
                         // whose mid-point lies on the bisector                       
                         void                                     perpendicularBisectorFromLine(pdd P, pdd Q,                       
                                                 double                                     &a,                                     double                                     &b,                                     double                                     &c)                       
                         {                       
                                                 pdd mid_point = make_pair((P.first + Q.first)/2,                       
                                                 (P.second + Q.second)/2);                       
           
                                                 // c = -bx + ay                       
                                                 c = -b*(mid_point.first) + a*(mid_point.second);                       
           
                                                 double                                     temp = a;                       
                                                 a = -b;                       
                                                 b = temp;                       
                         }                       
           
                         // Returns the intersection point of two lines                       
                         pdd lineLineIntersection(                                     double                                     a1,                                     double                                     b1,                                     double                                     c1,                       
                                                 double                                     a2,                                     double                                     b2,                                     double                                     c2)                       
                         {                       
                                                 double                                     determinant = a1*b2 - a2*b1;                       
                                                 if                                     (determinant == 0)                       
                                                 {                       
                                                 // The lines are parallel. This is simplified                       
                                                 // by returning a pair of FLT_MAX                       
                                                 return                                     make_pair(FLT_MAX, FLT_MAX);                       
                                                 }                       
           
                                                 else                       
                                                 {                       
                                                 double                                     x = (b2*c1 - b1*c2)/determinant;                       
                                                 double                                     y = (a1*c2 - a2*c1)/determinant;                       
                                                 return                                     make_pair(x, y);                       
                                                 }                       
                         }                       
           
                         void                                     findCircumCenter(pdd P, pdd Q, pdd R)                       
                         {                       
                                                 // Line PQ is represented as ax + by = c                       
                                                 double                                     a, b, c;                       
                                                 lineFromPoints(P, Q, a, b, c);                       
           
                                                 // Line QR is represented as ex + fy = g                       
                                                 double                                     e, f, g;                       
                                                 lineFromPoints(Q, R, e, f, g);                       
           
                                                 // Converting lines PQ and QR to perpendicular                       
                                                 // vbisectors. After this, L = ax + by = c                       
                                                 // M = ex + fy = g                       
                                                 perpendicularBisectorFromLine(P, Q, a, b, c);                       
                                                 perpendicularBisectorFromLine(Q, R, e, f, g);                       
           
                                                 // The point of intersection of L and M gives                       
                                                 // the circumcenter                       
                                                 pdd circumcenter =                       
                                                 lineLineIntersection(a, b, c, e, f, g);                       
           
                                                 if                                     (circumcenter.first == FLT_MAX &&                       
                                                 circumcenter.second == FLT_MAX)                       
                                                 {                       
                                                 cout <<                                     "The two perpendicular bisectors "                       
                                                 "found come parallel"                                     << endl;                       
                                                 cout <<                                     "Thus, the given points do not form "                       
                                                 "a triangle and are collinear"                                     << endl;                       
                                                 }                       
           
                                                 else                       
                                                 {                       
                                                 cout <<                                     "The circumcenter of the triangle PQR is: "                                     ;                       
                                                 cout <<                                     "("                                     << circumcenter.first <<                                     ", "                       
                                                 << circumcenter.second  <<                                     ")"                                     << endl;                       
                                                 }                       
                         }                       
           
                         // Driver code.                       
                         int                                     main()                       
                         {                       
                                                 pdd P = make_pair(6, 0);                       
                                                 pdd Q = make_pair(0, 0);                       
                                                 pdd R = make_pair(0, 8);                       
                                                 findCircumCenter(P, Q, R);                       
                                                 return                                     0;                       
                         }                       

Python3

                         # Python3 program to find the CIRCUMCENTER of a                       
                         # triangle                       
           
                         # This pair is used to store the X and Y                       
                         # coordinate of a point respectively                       
                         # define pair<double, double>                       
           
                         # Function to find the line given two points                       
                         def                                     lineFromPoints(P, Q, a, b, c):                       
                                                 a                                     =                                     Q[                                     1                                     ]                                     -                                     P[                                     1                                     ]                       
                                                 b                                     =                                     P[                                     0                                     ]                                     -                                     Q[                                     0                                     ]                       
                                                 c                                     =                                     a                                     *                                     (P[                                     0                                     ])                                     +                                     b                                     *                                     (P[                                     1                                     ])                       
                                                 return                                     a, b, c                       
           
                         # Function which converts the input line to its                       
                         # perpendicular bisector. It also inputs the points                       
                         # whose mid-point lies on the bisector                       
                         def                                     perpendicularBisectorFromLine(P, Q, a, b, c):                       
                                                 mid_point                                     =                                     [(P[                                     0                                     ]                                     +                                     Q[                                     0                                     ])                                     /                                     /                                     2                                     , (P[                                     1                                     ]                                     +                                     Q[                                     1                                     ])                                     /                                     /                                     2                                     ]                       
           
                                                 # c = -bx + ay                       
                                                 c                                     =                                     -                                     b                                     *                                     (mid_point[                                     0                                     ])                                     +                                     a                                     *                                     (mid_point[                                     1                                     ])                       
                                                 temp                                     =                                     a                       
                                                 a                                     =                                     -                                     b                       
                                                 b                                     =                                     temp                       
                                                 return                                     a, b, c                       
           
                         # Returns the intersection point of two lines                       
                         def                                     lineLineIntersection(a1, b1, c1, a2, b2, c2):                       
                                                 determinant                                     =                                     a1                                     *                                     b2                                     -                                     a2                                     *                                     b1                       
                                                 if                                     (determinant                                     =                                     =                                     0                                     ):                       
                                   
                                                 # The lines are parallel. This is simplified                       
                                                 # by returning a pair of (10.0)**19                       
                                                 return                                     [(                                     10.0                                     )                                     *                                     *                                     19                                     , (                                     10.0                                     )                                     *                                     *                                     19                                     ]                       
                                                 else                                     :                       
                                                 x                                     =                                     (b2                                     *                                     c1                                     -                                     b1                                     *                                     c2)                                     /                                     /                                     determinant                       
                                                 y                                     =                                     (a1                                     *                                     c2                                     -                                     a2                                     *                                     c1)                                     /                                     /                                     determinant                       
                                                 return                                     [x, y]                       
           
                         def                                     findCircumCenter(P, Q, R):                       
                                   
                                                 # Line PQ is represented as ax + by = c                       
                                                 a, b, c                                     =                                     0.0                                     ,                                     0.0                                     ,                                     0.0                       
                                                 a, b, c                                     =                                     lineFromPoints(P, Q, a, b, c)                       
           
                                                 # Line QR is represented as ex + fy = g                       
                                                 e, f, g                                     =                                     0.0                                     ,                                     0.0                                     ,                                     0.0                       
                                                 e, f, g                                     =                                     lineFromPoints(Q, R, e, f, g)                       
           
                                                 # Converting lines PQ and QR to perpendicular                       
                                                 # vbisectors. After this, L = ax + by = c                       
                                                 # M = ex + fy = g                       
                                                 a, b, c                                     =                                     perpendicularBisectorFromLine(P, Q, a, b, c)                       
                                                 e, f, g                                     =                                     perpendicularBisectorFromLine(Q, R, e, f, g)                       
           
                                                 # The point of intersection of L and M gives                       
                                                 # the circumcenter                       
                                                 circumcenter                                     =                                     lineLineIntersection(a, b, c, e, f, g)                       
           
                                                 if                                     (circumcenter[                                     0                                     ]                                     =                                     =                                     (                                     10.0                                     )                                     *                                     *                                     19                                     and                                     circumcenter[                                     1                                     ]                                     =                                     =                                     (                                     10.0                                     )                                     *                                     *                                     19                                     ):                       
                                                 print                                     (                                     "The two perpendicular bisectors found come parallel"                                     )                       
                                                 print                                     (                                     "Thus, the given points do not form a triangle and are collinear"                                     )                       
                                                 else                                     :                       
                                                 print                                     (                                     "The circumcenter of the triangle PQR is: "                                     , end                                     =                                     "")                       
                                                 print                                     (                                     "("                                     , circumcenter[                                     0                                     ],                                     ","                                     , circumcenter[                                     1                                     ],                                     ")"                                     )                       
           
                         # Driver code.                       
                         if                                     __name__                                     =                                     =                                     '__main__'                                     :                       
                                                 P                                     =                                     [                                     6                                     ,                                     0                                     ]                       
                                                 Q                                     =                                     [                                     0                                     ,                                     0                                     ]                       
                                                 R                                     =                                     [                                     0                                     ,                                     8                                     ]                       
                                                 findCircumCenter(P, Q, R)                       
           
                                                 # This code is contributed by mohit kumar 29                       

输出：

The circumcenter of the triangle PQR is: (3, 4)

本文由 安雅·金达尔 .如果你喜欢GeekSforgek，并想贡献自己的力量，你也可以使用贡献极客。组织或者把你的文章寄到contribute@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上，并帮助其他极客。如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请写下评论。

文章版权归作者所有，未经允许请勿转载。

THE END

技术文章