有n栋房子排成一行，每栋房子都有一定的价值。一个小偷要偷走这些房子的最大价值，但他不能在两个相邻的房子里偷东西，因为偷来的房子的主人会告诉他的左右两个邻居。最大被盗价值是多少？ 例如：
null
Input: hval[] = {6, 7, 1, 3, 8, 2, 4}Output: 19Explanation: The thief will steal 6, 1, 8 and 4 from the house.Input: hval[] = {5, 3, 4, 11, 2}Output: 16Explanation: Thief will steal 5 and 11
天真的方法 : 给定一个数组，解决方案是在没有两个选定元素相邻的情况下找到最大和子序列。所以这个问题的解决方法是递归的。所以有两种情况。
- 如果选择了一个元素，则无法选择下一个元素。
- 如果未选择某个图元，则可以选择下一个图元。
递归方法的实现：
C++
// CPP program to find the maximum stolen value #include <iostream> using namespace std; // calculate the maximum stolen value int maxLoot( int *hval, int n) { // base case if (n < 0){ return 0 ; } if (n == 0){ return hval[0] ; } //if current element is pick then previous cannot be picked int pick = hval[n] + maxLoot(hval, n-2) ; //if current element is not picked then previous element is picked int notPick = maxLoot(hval, n-1) ; // return max of picked and not picked return max(pick, notPick) ; } // Driver to test above code int main() { int hval[] = {6, 7, 1, 3, 8, 2, 4}; int n = sizeof (hval)/ sizeof (hval[0]); cout << "Maximum loot possible : " << maxLoot(hval, n-1); return 0; } |
输出
Maximum loot possible : 19
复杂性分析
时间复杂性： O（2） N ).每个元素有两个选项可供选择和不可选择
空间复杂性： O（2） N ).递归堆栈空间的大小为2 N 所以空间复杂度是O（2） N ).
方法2： 动态规划：自上而下的方法
因此，递归解决方案可以很容易地设计出来。子问题可以存储，从而降低复杂性，并将递归解转换为动态规划问题。
C++
// CPP program to find the maximum stolen value #include <bits/stdc++.h> using namespace std; // calculate the maximum stolen value int maxLoot( int *hval, int n, vector< int > &dp){ // base case if (n < 0){ return 0 ; } if (n == 0){ return hval[0] ; } // If the subproblem is already solved // then return its value if (dp[n] != -1 ){ return dp[n] ; } //if current element is pick then previous cannot be picked int pick = hval[n] + maxLoot(hval, n-2, dp) ; //if current element is not picked then previous element is picked int notPick = maxLoot(hval, n-1, dp) ; // return max of picked and not picked return dp[n] = max(pick, notPick) ; } // Driver to test above code int main() { int hval[] = {6, 7, 1, 3, 8, 2, 4}; int n = sizeof (hval)/ sizeof (hval[0]); // Initialize a dp vector vector< int > dp(n+1, -1) ; cout << "Maximum loot possible : " << maxLoot(hval, n-1, dp); return 0; } |
输出
Maximum loot possible : 19
复杂性分析：
时间复杂性： O（n）。只需要遍历原始数组一次。所以时间复杂度是O（n）
空间复杂性： O（n）。递归堆栈空间的大小要求为n，因此空间复杂度为O（n）。
方法3： 动态规划：自下而上的方法
因此，递归解决方案可以很容易地设计出来。子问题可以存储，从而降低复杂性，并将递归解转换为动态规划问题。
算法：
- 创造一个额外的空间 数据处理 ，DP数组来存储子问题。
- 处理一些基本情况，如果数组长度为0，则打印0，如果数组长度为1，则打印第一个元素，如果数组长度为2，则打印最多两个元素。
- 使现代化 dp[0] 像 数组[0] 和 dp[1] 最多 数组[0] 和 数组[1]
- 从第二个元素（第二个索引）到数组末尾遍历数组。
- 对于每个索引，更新 dp[i] 最多 dp[i-2]+阵列[i] 和 dp[i-1] ，此步骤定义了两种情况，如果选择了一个元素，则无法选择上一个元素；如果未选择元素，则可以选择上一个元素。
- 打印值 dp[n-1]
实施：
C++
// CPP program to find the maximum stolen value #include <iostream> using namespace std; // calculate the maximum stolen value int maxLoot( int *hval, int n) { if (n == 0) return 0; if (n == 1) return hval[0]; if (n == 2) return max(hval[0], hval[1]); // dp[i] represent the maximum value stolen // so far after reaching house i. int dp[n]; // Initialize the dp[0] and dp[1] dp[0] = hval[0]; dp[1] = max(hval[0], hval[1]); // Fill remaining positions for ( int i = 2; i<n; i++) dp[i] = max(hval[i]+dp[i-2], dp[i-1]); return dp[n-1]; } // Driver to test above code int main() { int hval[] = {6, 7, 1, 3, 8, 2, 4}; int n = sizeof (hval)/ sizeof (hval[0]); cout << "Maximum loot possible : " << maxLoot(hval, n); return 0; } |
JAVA
// Java program to find the maximum stolen value import java.io.*; class GFG { // Function to calculate the maximum stolen value static int maxLoot( int hval[], int n) { if (n == 0 ) return 0 ; if (n == 1 ) return hval[ 0 ]; if (n == 2 ) return Math.max(hval[ 0 ], hval[ 1 ]); // dp[i] represent the maximum value stolen // so far after reaching house i. int [] dp = new int [n]; // Initialize the dp[0] and dp[1] dp[ 0 ] = hval[ 0 ]; dp[ 1 ] = Math.max(hval[ 0 ], hval[ 1 ]); // Fill remaining positions for ( int i = 2 ; i<n; i++) dp[i] = Math.max(hval[i]+dp[i- 2 ], dp[i- 1 ]); return dp[n- 1 ]; } // Driver program public static void main (String[] args) { int hval[] = { 6 , 7 , 1 , 3 , 8 , 2 , 4 }; int n = hval.length; System.out.println( "Maximum loot value : " + maxLoot(hval, n)); } } // Contributed by Pramod Kumar |
Python3
# Python3 program to find the maximum stolen value # calculate the maximum stolen value def maximize_loot(hval, n): if n = = 0 : return 0 if n = = 1 : return hval[ 0 ] if n = = 2 : return max (hval[ 0 ], hval[ 1 ]) # dp[i] represent the maximum value stolen so # for after reaching house i. dp = [ 0 ] * n # Initialize the dp[0] and dp[1] dp[ 0 ] = hval[ 0 ] dp[ 1 ] = max (hval[ 0 ], hval[ 1 ]) # Fill remaining positions for i in range ( 2 , n): dp[i] = max (hval[i] + dp[i - 2 ], dp[i - 1 ]) return dp[ - 1 ] # Driver to test above code def main(): # Value of houses hval = [ 6 , 7 , 1 , 3 , 8 , 2 , 4 ] # number of houses n = len (hval) print ( "Maximum loot value : {}" . format (maximize_loot(hval, n))) if __name__ = = '__main__' : main() |
C#
// C# program to find the // maximum stolen value using System; class GFG { // Function to calculate the // maximum stolen value static int maxLoot( int []hval, int n) { if (n == 0) return 0; if (n == 1) return hval[0]; if (n == 2) return Math.Max(hval[0], hval[1]); // dp[i] represent the maximum value stolen // so far after reaching house i. int [] dp = new int [n]; // Initialize the dp[0] and dp[1] dp[0] = hval[0]; dp[1] = Math.Max(hval[0], hval[1]); // Fill remaining positions for ( int i = 2; i<n; i++) dp[i] = Math.Max(hval[i]+dp[i-2], dp[i-1]); return dp[n-1]; } // Driver program public static void Main () { int []hval = {6, 7, 1, 3, 8, 2, 4}; int n = hval.Length; Console.WriteLine( "Maximum loot value : " + maxLoot(hval, n)); } } // This code is contributed by Sam007 |
PHP
<?php // PHP program to find // the maximum stolen value // calculate the maximum // stolen value function maxLoot( $hval , $n ) { if ( $n == 0) return 0; if ( $n == 1) return $hval [0]; if ( $n == 2) return max( $hval [0], $hval [1]); // dp[i] represent the maximum // value stolen so far after // reaching house i. $dp = array (); // Initialize the // dp[0] and dp[1] $dp [0] = $hval [0]; $dp [1] = max( $hval [0], $hval [1]); // Fill remaining positions for ( $i = 2; $i < $n ; $i ++) $dp [ $i ] = max( $hval [ $i ] + $dp [ $i - 2], $dp [ $i - 1]); return $dp [ $n - 1]; } // Driver Code $hval = array (6, 7, 1, 3, 8, 2, 4); $n = sizeof( $hval ); echo "Maximum loot possible : " , maxLoot( $hval , $n ); // This code is contributed by aj_36 ?> |
Javascript
<script> // Javascript program to find // the maximum stolen value // Function to calculate the // maximum stolen value function maxLoot(hval, n) { if (n == 0) return 0; if (n == 1) return hval[0]; if (n == 2) return Math.max(hval[0], hval[1]); // dp[i] represent the maximum value stolen // so far after reaching house i. let dp = new Array(n); // Initialize the dp[0] and dp[1] dp[0] = hval[0]; dp[1] = Math.max(hval[0], hval[1]); // Fill remaining positions for (let i = 2; i<n; i++) dp[i] = Math.max(hval[i]+dp[i-2], dp[i-1]); return dp[n-1]; } let hval = [6, 7, 1, 3, 8, 2, 4]; let n = hval.length; document.write( "Maximum loot value : " + maxLoot(hval, n) ); </script> |
输出
Maximum loot possible : 19
复杂性分析：
- 时间复杂性：
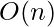. 只需要遍历原始数组一次。所以时间复杂度是O（n） - 空间复杂性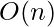： . 数组的大小要求为n，因此空间复杂度为O（n）。
有效方法： 通过仔细观察DP数组，可以看出，在计算某个索引的值时，前两个索引的值很重要。用两个变量替换总DP数组。
算法：
- 处理一些基本情况，如果数组长度为0，则打印0，如果数组长度为1，则打印第一个元素，如果数组长度为2，则打印最多两个元素。
- 创建两个变量 价值1 和 价值2 价值1 像 数组[0] 和 价值2 最多 数组[0] 和 数组[1] 还有一个变量 麦克斯瓦尔 储存答案
- 从第二个元素（第二个索引）到数组末尾遍历数组。
- 对于每个索引，更新 麦克斯瓦尔 最多 value1+数组[i] 和 价值2 ，此步骤定义了两种情况，如果选择了一个元素，则无法选择上一个元素；如果未选择一个元素，则可以选择上一个元素。
- 对于每个索引，更新 value1=value2 和 值2=最大值
- 打印 麦克斯瓦尔
实施：
C++
// C++ program to find the maximum stolen value #include <iostream> using namespace std; // calculate the maximum stolen value int maxLoot( int *hval, int n) { if (n == 0) return 0; int value1 = hval[0]; if (n == 1) return value1; int value2 = max(hval[0], hval[1]); if (n == 2) return value2; // contains maximum stolen value at the end int max_val; // Fill remaining positions for ( int i=2; i<n; i++) { max_val = max(hval[i]+value1, value2); value1 = value2; value2 = max_val; } return max_val; } // Driver to test above code int main() { // Value of houses int hval[] = {6, 7, 1, 3, 8, 2, 4}; int n = sizeof (hval)/ sizeof (hval[0]); cout << "Maximum loot possible : " << maxLoot(hval, n); return 0; } |
JAVA
// Java program to find the maximum stolen value import java.io.*; class GFG { // Function to calculate the maximum stolen value static int maxLoot( int hval[], int n) { if (n == 0 ) return 0 ; int value1 = hval[ 0 ]; if (n == 1 ) return value1; int value2 = Math.max(hval[ 0 ], hval[ 1 ]); if (n == 2 ) return value2; // contains maximum stolen value at the end int max_val = 0 ; // Fill remaining positions for ( int i= 2 ; i<n; i++) { max_val = Math.max(hval[i]+value1, value2); value1 = value2; value2 = max_val; } return max_val; } // driver program public static void main (String[] args) { int hval[] = { 6 , 7 , 1 , 3 , 8 , 2 , 4 }; int n = hval.length; System.out.println( "Maximum loot value : " + maxLoot(hval, n)); } } // Contributed by Pramod kumar |
Python3
# Python3 program to find the maximum stolen value # calculate the maximum stolen value def maximize_loot(hval, n): if n = = 0 : return 0 value1 = hval[ 0 ] if n = = 1 : return value1 value2 = max (hval[ 0 ], hval[ 1 ]) if n = = 2 : return value2 # contains maximum stolen value at the end max_val = None # Fill remaining positions for i in range ( 2 , n): max_val = max (hval[i] + value1, value2) value1 = value2 value2 = max_val return max_val # Driver to test above code def main(): # Value of houses hval = [ 6 , 7 , 1 , 3 , 8 , 2 , 4 ] # number of houses n = len (hval) print ( "Maximum loot value : {}" . format (maximize_loot(hval, n))) if __name__ = = '__main__' : main() |
C#
// C# program to find the // maximum stolen value using System; public class GFG { // Function to calculate the // maximum stolen value static int maxLoot( int []hval, int n) { if (n == 0) return 0; int value1 = hval[0]; if (n == 1) return value1; int value2 = Math.Max(hval[0], hval[1]); if (n == 2) return value2; // contains maximum stolen value at the end int max_val = 0; // Fill remaining positions for ( int i = 2; i < n; i++) { max_val = Math.Max(hval[i] + value1, value2); value1 = value2; value2 = max_val; } return max_val; } // Driver program public static void Main () { int []hval = {6, 7, 1, 3, 8, 2, 4}; int n = hval.Length; Console.WriteLine( "Maximum loot value : " + maxLoot(hval, n)); } } // This code is contributed by Sam007 |
PHP
<?php // PHP program to find // the maximum stolen value // calculate the // maximum stolen value function maxLoot( $hval , $n ) { if ( $n == 0) return 0; $value1 = $hval [0]; if ( $n == 1) return $value1 ; $value2 = max( $hval [0], $hval [1]); if ( $n == 2) return $value2 ; // contains maximum // stolen value at the end $max_val ; // Fill remaining positions for ( $i = 2; $i < $n ; $i ++) { $max_val = max( $hval [ $i ] + $value1 , $value2 ); $value1 = $value2 ; $value2 = $max_val ; } return $max_val ; } // Driver code $hval = array (6, 7, 1, 3, 8, 2, 4); $n = sizeof( $hval ); echo "Maximum loot value : " , maxLoot( $hval , $n ); // This code is contributed by ajit ?> |
Javascript
<script> // Javascript program to find the // maximum stolen value // Function to calculate the // maximum stolen value function maxLoot(hval, n) { if (n == 0) return 0; let value1 = hval[0]; if (n == 1) return value1; let value2 = Math.max(hval[0], hval[1]); if (n == 2) return value2; // contains maximum stolen value at the end let max_val = 0; // Fill remaining positions for (let i = 2; i < n; i++) { max_val = Math.max(hval[i] + value1, value2); value1 = value2; value2 = max_val; } return max_val; } let hval = [6, 7, 1, 3, 8, 2, 4]; let n = hval.length; document.write( "Maximum loot value : " + maxLoot(hval, n)); </script> |
输出
Maximum loot possible : 19
复杂性分析：
- 时间复杂性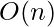： ，只需遍历原始数组一次。所以时间复杂度是O（n）。
- 辅助空间：
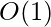，不需要额外的空间，因此空间复杂度是恒定的。
本文由 阿图尔·库马尔 .如果你喜欢GeekSforgek，并想贡献自己的力量，你也可以使用 贡献极客。组织 或者把你的文章寄去评论-team@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上，并帮助其他极客。 如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请写下评论。
© 版权声明
文章版权归作者所有，未经允许请勿转载。
THE END
![关于”PostgreSQL错误：关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)
