先决条件: 博弈论中的极小极大算法 , 博弈论中的评价函数 让我们结合到目前为止所学的关于极小极大和求值函数的知识来编写一个合适的Tic-Tac-Toe 人工智能 ( A. 人工的 我 智能)玩一个完美的游戏。这个人工智能将考虑所有可能的情况,并做出最佳的移动。
寻找最佳行动:
我们将引入一个名为 findBestMove() 。此函数使用 极小极大() 然后返回最大化者能做出的最佳动作。伪代码如下:
function findBestMove(board): bestMove = NULL for each move in board : if current move is better than bestMove bestMove = current move return bestMove
极小极大值:
检查目前的行动是否比我们帮助的最佳行动更好 极小极大() 函数将考虑所有可能的方式游戏可以去,并返回最佳值的移动,假设对手也发挥最佳
中最大值和最小值的代码 极小极大() 功能类似于 findBestMove() ,唯一的区别是,它不会返回移动,而是返回一个值。以下是伪代码:
function minimax(board, depth, isMaximizingPlayer): if current board state is a terminal state : return value of the board if isMaximizingPlayer : bestVal = -INFINITY for each move in board : value = minimax(board, depth+1, false) bestVal = max( bestVal, value) return bestVal else : bestVal = +INFINITY for each move in board : value = minimax(board, depth+1, true) bestVal = min( bestVal, value) return bestVal
正在检查GameOver状态:
检查游戏是否结束,并确保没有我们使用的移动 isMovesLeft() 作用这是一个简单明了的函数,用于检查移动是否可用,并分别返回true或false。伪代码如下:
function isMovesLeft(board): for each cell in board: if current cell is empty: return true return false
让我们的人工智能更智能:
最后一步是让我们的人工智能更智能一点。即使下面的人工智能玩得很完美,它可能会选择采取行动,这将导致较慢的胜利或更快的损失。让我们举个例子来解释一下。 假设在给定的棋盘状态下,X有两种可能的获胜方式。
- 移动 A. :X可以在两步中获胜
- 移动 B :X可以在4步中获胜
我们的求值函数将为两个移动返回+10的值 A. 和 B .即使搬家 A. 更好是因为它确保了更快的胜利,我们的人工智能可以选择 B 有时为了克服这个问题,我们从评估的分数中减去深度值。这意味着,如果获胜,它将选择一个移动次数最少的胜利,如果失败,它将尝试延长游戏时间,并尽可能多地使用移动。因此,新的评估值将是
- 移动 A. 将具有+10–2=8的值
- 移动 B 将具有+10–4=6的值
自从搬家以来 A. 比move得分更高 B 我们的人工智能将选择移动 A. 过度移动 B .同样的道理也必须适用于极小化。我们不是减去深度,而是加上深度值,因为最小值总是试图得到尽可能负的值。我们可以在求值函数内部或外部减去深度。任何地方都可以。我选择在功能之外做这件事。伪代码实现如下。
if maximizer has won: return WIN_SCORE – depthelse if minimizer has won: return LOOSE_SCORE + depth
下面是上述想法的实现。
C++
// C++ program to find the next optimal move for // a player #include<bits/stdc++.h> using namespace std; struct Move { int row, col; }; char player = 'x' , opponent = 'o' ; // This function returns true if there are moves // remaining on the board. It returns false if // there are no moves left to play. bool isMovesLeft( char board[3][3]) { for ( int i = 0; i<3; i++) for ( int j = 0; j<3; j++) if (board[i][j]== '_' ) return true ; return false ; } // This is the evaluation function as discussed // in the previous article ( http://goo.gl/sJgv68 ) int evaluate( char b[3][3]) { // Checking for Rows for X or O victory. for ( int row = 0; row<3; row++) { if (b[row][0]==b[row][1] && b[row][1]==b[row][2]) { if (b[row][0]==player) return +10; else if (b[row][0]==opponent) return -10; } } // Checking for Columns for X or O victory. for ( int col = 0; col<3; col++) { if (b[0][col]==b[1][col] && b[1][col]==b[2][col]) { if (b[0][col]==player) return +10; else if (b[0][col]==opponent) return -10; } } // Checking for Diagonals for X or O victory. if (b[0][0]==b[1][1] && b[1][1]==b[2][2]) { if (b[0][0]==player) return +10; else if (b[0][0]==opponent) return -10; } if (b[0][2]==b[1][1] && b[1][1]==b[2][0]) { if (b[0][2]==player) return +10; else if (b[0][2]==opponent) return -10; } // Else if none of them have won then return 0 return 0; } // This is the minimax function. It considers all // the possible ways the game can go and returns // the value of the board int minimax( char board[3][3], int depth, bool isMax) { int score = evaluate(board); // If Maximizer has won the game return his/her // evaluated score if (score == 10) return score; // If Minimizer has won the game return his/her // evaluated score if (score == -10) return score; // If there are no more moves and no winner then // it is a tie if (isMovesLeft(board)== false ) return 0; // If this maximizer's move if (isMax) { int best = -1000; // Traverse all cells for ( int i = 0; i<3; i++) { for ( int j = 0; j<3; j++) { // Check if cell is empty if (board[i][j]== '_' ) { // Make the move board[i][j] = player; // Call minimax recursively and choose // the maximum value best = max( best, minimax(board, depth+1, !isMax) ); // Undo the move board[i][j] = '_' ; } } } return best; } // If this minimizer's move else { int best = 1000; // Traverse all cells for ( int i = 0; i<3; i++) { for ( int j = 0; j<3; j++) { // Check if cell is empty if (board[i][j]== '_' ) { // Make the move board[i][j] = opponent; // Call minimax recursively and choose // the minimum value best = min(best, minimax(board, depth+1, !isMax)); // Undo the move board[i][j] = '_' ; } } } return best; } } // This will return the best possible move for the player Move findBestMove( char board[3][3]) { int bestVal = -1000; Move bestMove; bestMove.row = -1; bestMove.col = -1; // Traverse all cells, evaluate minimax function for // all empty cells. And return the cell with optimal // value. for ( int i = 0; i<3; i++) { for ( int j = 0; j<3; j++) { // Check if cell is empty if (board[i][j]== '_' ) { // Make the move board[i][j] = player; // compute evaluation function for this // move. int moveVal = minimax(board, 0, false ); // Undo the move board[i][j] = '_' ; // If the value of the current move is // more than the best value, then update // best/ if (moveVal > bestVal) { bestMove.row = i; bestMove.col = j; bestVal = moveVal; } } } } printf ( "The value of the best Move is : %d" , bestVal); return bestMove; } // Driver code int main() { char board[3][3] = { { 'x' , 'o' , 'x' }, { 'o' , 'o' , 'x' }, { '_' , '_' , '_' } }; Move bestMove = findBestMove(board); printf ( "The Optimal Move is :" ); printf ( "ROW: %d COL: %d" , bestMove.row, bestMove.col ); return 0; } |
JAVA
// Java program to find the // next optimal move for a player class GFG { static class Move { int row, col; }; static char player = 'x' , opponent = 'o' ; // This function returns true if there are moves // remaining on the board. It returns false if // there are no moves left to play. static Boolean isMovesLeft( char board[][]) { for ( int i = 0 ; i < 3 ; i++) for ( int j = 0 ; j < 3 ; j++) if (board[i][j] == '_' ) return true ; return false ; } // This is the evaluation function as discussed // in the previous article ( http://goo.gl/sJgv68 ) static int evaluate( char b[][]) { // Checking for Rows for X or O victory. for ( int row = 0 ; row < 3 ; row++) { if (b[row][ 0 ] == b[row][ 1 ] && b[row][ 1 ] == b[row][ 2 ]) { if (b[row][ 0 ] == player) return + 10 ; else if (b[row][ 0 ] == opponent) return - 10 ; } } // Checking for Columns for X or O victory. for ( int col = 0 ; col < 3 ; col++) { if (b[ 0 ][col] == b[ 1 ][col] && b[ 1 ][col] == b[ 2 ][col]) { if (b[ 0 ][col] == player) return + 10 ; else if (b[ 0 ][col] == opponent) return - 10 ; } } // Checking for Diagonals for X or O victory. if (b[ 0 ][ 0 ] == b[ 1 ][ 1 ] && b[ 1 ][ 1 ] == b[ 2 ][ 2 ]) { if (b[ 0 ][ 0 ] == player) return + 10 ; else if (b[ 0 ][ 0 ] == opponent) return - 10 ; } if (b[ 0 ][ 2 ] == b[ 1 ][ 1 ] && b[ 1 ][ 1 ] == b[ 2 ][ 0 ]) { if (b[ 0 ][ 2 ] == player) return + 10 ; else if (b[ 0 ][ 2 ] == opponent) return - 10 ; } // Else if none of them have won then return 0 return 0 ; } // This is the minimax function. It considers all // the possible ways the game can go and returns // the value of the board static int minimax( char board[][], int depth, Boolean isMax) { int score = evaluate(board); // If Maximizer has won the game // return his/her evaluated score if (score == 10 ) return score; // If Minimizer has won the game // return his/her evaluated score if (score == - 10 ) return score; // If there are no more moves and // no winner then it is a tie if (isMovesLeft(board) == false ) return 0 ; // If this maximizer's move if (isMax) { int best = - 1000 ; // Traverse all cells for ( int i = 0 ; i < 3 ; i++) { for ( int j = 0 ; j < 3 ; j++) { // Check if cell is empty if (board[i][j]== '_' ) { // Make the move board[i][j] = player; // Call minimax recursively and choose // the maximum value best = Math.max(best, minimax(board, depth + 1 , !isMax)); // Undo the move board[i][j] = '_' ; } } } return best; } // If this minimizer's move else { int best = 1000 ; // Traverse all cells for ( int i = 0 ; i < 3 ; i++) { for ( int j = 0 ; j < 3 ; j++) { // Check if cell is empty if (board[i][j] == '_' ) { // Make the move board[i][j] = opponent; // Call minimax recursively and choose // the minimum value best = Math.min(best, minimax(board, depth + 1 , !isMax)); // Undo the move board[i][j] = '_' ; } } } return best; } } // This will return the best possible // move for the player static Move findBestMove( char board[][]) { int bestVal = - 1000 ; Move bestMove = new Move(); bestMove.row = - 1 ; bestMove.col = - 1 ; // Traverse all cells, evaluate minimax function // for all empty cells. And return the cell // with optimal value. for ( int i = 0 ; i < 3 ; i++) { for ( int j = 0 ; j < 3 ; j++) { // Check if cell is empty if (board[i][j] == '_' ) { // Make the move board[i][j] = player; // compute evaluation function for this // move. int moveVal = minimax(board, 0 , false ); // Undo the move board[i][j] = '_' ; // If the value of the current move is // more than the best value, then update // best/ if (moveVal > bestVal) { bestMove.row = i; bestMove.col = j; bestVal = moveVal; } } } } System.out.printf( "The value of the best Move " + "is : %d" , bestVal); return bestMove; } // Driver code public static void main(String[] args) { char board[][] = {{ 'x' , 'o' , 'x' }, { 'o' , 'o' , 'x' }, { '_' , '_' , '_' }}; Move bestMove = findBestMove(board); System.out.printf( "The Optimal Move is :" ); System.out.printf( "ROW: %d COL: %d" , bestMove.row, bestMove.col ); } } // This code is contributed by PrinciRaj1992 |
Python3
# Python3 program to find the next optimal move for a player player, opponent = 'x' , 'o' # This function returns true if there are moves # remaining on the board. It returns false if # there are no moves left to play. def isMovesLeft(board) : for i in range ( 3 ) : for j in range ( 3 ) : if (board[i][j] = = '_' ) : return True return False # This is the evaluation function as discussed # in the previous article ( http://goo.gl/sJgv68 ) def evaluate(b) : # Checking for Rows for X or O victory. for row in range ( 3 ) : if (b[row][ 0 ] = = b[row][ 1 ] and b[row][ 1 ] = = b[row][ 2 ]) : if (b[row][ 0 ] = = player) : return 10 else if (b[row][ 0 ] = = opponent) : return - 10 # Checking for Columns for X or O victory. for col in range ( 3 ) : if (b[ 0 ][col] = = b[ 1 ][col] and b[ 1 ][col] = = b[ 2 ][col]) : if (b[ 0 ][col] = = player) : return 10 else if (b[ 0 ][col] = = opponent) : return - 10 # Checking for Diagonals for X or O victory. if (b[ 0 ][ 0 ] = = b[ 1 ][ 1 ] and b[ 1 ][ 1 ] = = b[ 2 ][ 2 ]) : if (b[ 0 ][ 0 ] = = player) : return 10 else if (b[ 0 ][ 0 ] = = opponent) : return - 10 if (b[ 0 ][ 2 ] = = b[ 1 ][ 1 ] and b[ 1 ][ 1 ] = = b[ 2 ][ 0 ]) : if (b[ 0 ][ 2 ] = = player) : return 10 else if (b[ 0 ][ 2 ] = = opponent) : return - 10 # Else if none of them have won then return 0 return 0 # This is the minimax function. It considers all # the possible ways the game can go and returns # the value of the board def minimax(board, depth, isMax) : score = evaluate(board) # If Maximizer has won the game return his/her # evaluated score if (score = = 10 ) : return score # If Minimizer has won the game return his/her # evaluated score if (score = = - 10 ) : return score # If there are no more moves and no winner then # it is a tie if (isMovesLeft(board) = = False ) : return 0 # If this maximizer's move if (isMax) : best = - 1000 # Traverse all cells for i in range ( 3 ) : for j in range ( 3 ) : # Check if cell is empty if (board[i][j] = = '_' ) : # Make the move board[i][j] = player # Call minimax recursively and choose # the maximum value best = max ( best, minimax(board, depth + 1 , not isMax) ) # Undo the move board[i][j] = '_' return best # If this minimizer's move else : best = 1000 # Traverse all cells for i in range ( 3 ) : for j in range ( 3 ) : # Check if cell is empty if (board[i][j] = = '_' ) : # Make the move board[i][j] = opponent # Call minimax recursively and choose # the minimum value best = min (best, minimax(board, depth + 1 , not isMax)) # Undo the move board[i][j] = '_' return best # This will return the best possible move for the player def findBestMove(board) : bestVal = - 1000 bestMove = ( - 1 , - 1 ) # Traverse all cells, evaluate minimax function for # all empty cells. And return the cell with optimal # value. for i in range ( 3 ) : for j in range ( 3 ) : # Check if cell is empty if (board[i][j] = = '_' ) : # Make the move board[i][j] = player # compute evaluation function for this # move. moveVal = minimax(board, 0 , False ) # Undo the move board[i][j] = '_' # If the value of the current move is # more than the best value, then update # best/ if (moveVal > bestVal) : bestMove = (i, j) bestVal = moveVal print ( "The value of the best Move is :" , bestVal) print () return bestMove # Driver code board = [ [ 'x' , 'o' , 'x' ], [ 'o' , 'o' , 'x' ], [ '_' , '_' , '_' ] ] bestMove = findBestMove(board) print ( "The Optimal Move is :" ) print ( "ROW:" , bestMove[ 0 ], " COL:" , bestMove[ 1 ]) # This code is contributed by divyesh072019 |
C#
// C# program to find the // next optimal move for a player using System; using System.Collections.Generic; class GFG { class Move { public int row, col; }; static char player = 'x' , opponent = 'o' ; // This function returns true if there are moves // remaining on the board. It returns false if // there are no moves left to play. static Boolean isMovesLeft( char [,]board) { for ( int i = 0; i < 3; i++) for ( int j = 0; j < 3; j++) if (board[i, j] == '_' ) return true ; return false ; } // This is the evaluation function as discussed // in the previous article ( http://goo.gl/sJgv68 ) static int evaluate( char [,]b) { // Checking for Rows for X or O victory. for ( int row = 0; row < 3; row++) { if (b[row, 0] == b[row, 1] && b[row, 1] == b[row, 2]) { if (b[row, 0] == player) return +10; else if (b[row, 0] == opponent) return -10; } } // Checking for Columns for X or O victory. for ( int col = 0; col < 3; col++) { if (b[0, col] == b[1, col] && b[1, col] == b[2, col]) { if (b[0, col] == player) return +10; else if (b[0, col] == opponent) return -10; } } // Checking for Diagonals for X or O victory. if (b[0, 0] == b[1, 1] && b[1, 1] == b[2, 2]) { if (b[0, 0] == player) return +10; else if (b[0, 0] == opponent) return -10; } if (b[0, 2] == b[1, 1] && b[1, 1] == b[2, 0]) { if (b[0, 2] == player) return +10; else if (b[0, 2] == opponent) return -10; } // Else if none of them have won then return 0 return 0; } // This is the minimax function. It considers all // the possible ways the game can go and returns // the value of the board static int minimax( char [,]board, int depth, Boolean isMax) { int score = evaluate(board); // If Maximizer has won the game // return his/her evaluated score if (score == 10) return score; // If Minimizer has won the game // return his/her evaluated score if (score == -10) return score; // If there are no more moves and // no winner then it is a tie if (isMovesLeft(board) == false ) return 0; // If this maximizer's move if (isMax) { int best = -1000; // Traverse all cells for ( int i = 0; i < 3; i++) { for ( int j = 0; j < 3; j++) { // Check if cell is empty if (board[i, j] == '_' ) { // Make the move board[i, j] = player; // Call minimax recursively and choose // the maximum value best = Math.Max(best, minimax(board, depth + 1, !isMax)); // Undo the move board[i, j] = '_' ; } } } return best; } // If this minimizer's move else { int best = 1000; // Traverse all cells for ( int i = 0; i < 3; i++) { for ( int j = 0; j < 3; j++) { // Check if cell is empty if (board[i, j] == '_' ) { // Make the move board[i, j] = opponent; // Call minimax recursively and choose // the minimum value best = Math.Min(best, minimax(board, depth + 1, !isMax)); // Undo the move board[i, j] = '_' ; } } } return best; } } // This will return the best possible // move for the player static Move findBestMove( char [,]board) { int bestVal = -1000; Move bestMove = new Move(); bestMove.row = -1; bestMove.col = -1; // Traverse all cells, evaluate minimax function // for all empty cells. And return the cell // with optimal value. for ( int i = 0; i < 3; i++) { for ( int j = 0; j < 3; j++) { // Check if cell is empty if (board[i, j] == '_' ) { // Make the move board[i, j] = player; // compute evaluation function for this // move. int moveVal = minimax(board, 0, false ); // Undo the move board[i, j] = '_' ; // If the value of the current move is // more than the best value, then update // best/ if (moveVal > bestVal) { bestMove.row = i; bestMove.col = j; bestVal = moveVal; } } } } Console.Write( "The value of the best Move " + "is : {0}" , bestVal); return bestMove; } // Driver code public static void Main(String[] args) { char [,]board = {{ 'x' , 'o' , 'x' }, { 'o' , 'o' , 'x' }, { '_' , '_' , '_' }}; Move bestMove = findBestMove(board); Console.Write( "The Optimal Move is :" ); Console.Write( "ROW: {0} COL: {1}" , bestMove.row, bestMove.col ); } } // This code is contributed by 29AjayKumar |
Javascript
<script> // Javascript program to find the // next optimal move for a player class Move { constructor() { let row,col; } } let player = 'x' , opponent = 'o' ; // This function returns true if there are moves // remaining on the board. It returns false if // there are no moves left to play. function isMovesLeft(board) { for (let i = 0; i < 3; i++) for (let j = 0; j < 3; j++) if (board[i][j] == '_' ) return true ; return false ; } // This is the evaluation function as discussed // in the previous article ( http://goo.gl/sJgv68 ) function evaluate(b) { // Checking for Rows for X or O victory. for (let row = 0; row < 3; row++) { if (b[row][0] == b[row][1] && b[row][1] == b[row][2]) { if (b[row][0] == player) return +10; else if (b[row][0] == opponent) return -10; } } // Checking for Columns for X or O victory. for (let col = 0; col < 3; col++) { if (b[0][col] == b[1][col] && b[1][col] == b[2][col]) { if (b[0][col] == player) return +10; else if (b[0][col] == opponent) return -10; } } // Checking for Diagonals for X or O victory. if (b[0][0] == b[1][1] && b[1][1] == b[2][2]) { if (b[0][0] == player) return +10; else if (b[0][0] == opponent) return -10; } if (b[0][2] == b[1][1] && b[1][1] == b[2][0]) { if (b[0][2] == player) return +10; else if (b[0][2] == opponent) return -10; } // Else if none of them have // won then return 0 return 0; } // This is the minimax function. It // considers all the possible ways // the game can go and returns the // value of the board function minimax(board, depth, isMax) { let score = evaluate(board); // If Maximizer has won the game // return his/her evaluated score if (score == 10) return score; // If Minimizer has won the game // return his/her evaluated score if (score == -10) return score; // If there are no more moves and // no winner then it is a tie if (isMovesLeft(board) == false ) return 0; // If this maximizer's move if (isMax) { let best = -1000; // Traverse all cells for (let i = 0; i < 3; i++) { for (let j = 0; j < 3; j++) { // Check if cell is empty if (board[i][j]=='_ ') { // Make the move board[i][j] = player; // Call minimax recursively // and choose the maximum value best = Math.max(best, minimax(board, depth + 1, !isMax)); // Undo the move board[i][j] = ' _ '; } } } return best; } // If this minimizer' s move else { let best = 1000; // Traverse all cells for (let i = 0; i < 3; i++) { for (let j = 0; j < 3; j++) { // Check if cell is empty if (board[i][j] == '_' ) { // Make the move board[i][j] = opponent; // Call minimax recursively and // choose the minimum value best = Math.min(best, minimax(board, depth + 1, !isMax)); // Undo the move board[i][j] = '_' ; } } } return best; } } // This will return the best possible // move for the player function findBestMove(board) { let bestVal = -1000; let bestMove = new Move(); bestMove.row = -1; bestMove.col = -1; // Traverse all cells, evaluate // minimax function for all empty // cells. And return the cell // with optimal value. for (let i = 0; i < 3; i++) { for (let j = 0; j < 3; j++) { // Check if cell is empty if (board[i][j] == '_' ) { // Make the move board[i][j] = player; // compute evaluation function // for this move. let moveVal = minimax(board, 0, false ); // Undo the move board[i][j] = '_' ; // If the value of the current move // is more than the best value, then // update best if (moveVal > bestVal) { bestMove.row = i; bestMove.col = j; bestVal = moveVal; } } } } document.write( "The value of the best Move " + "is : " , bestVal + "<br><br>" ); return bestMove; } // Driver code let board = [ [ 'x' , 'o' , 'x' ], [ 'o' , 'o' , 'x' ], [ '_' , '_' , '_' ] ]; let bestMove = findBestMove(board); document.write( "The Optimal Move is :<br>" ); document.write( "ROW: " + bestMove.row + " COL: " + bestMove.col + "<br>" ); // This code is contributed by rag2127 </script> |
输出:
The value of the best Move is : 10The Optimal Move is :ROW: 2 COL: 2
说明:
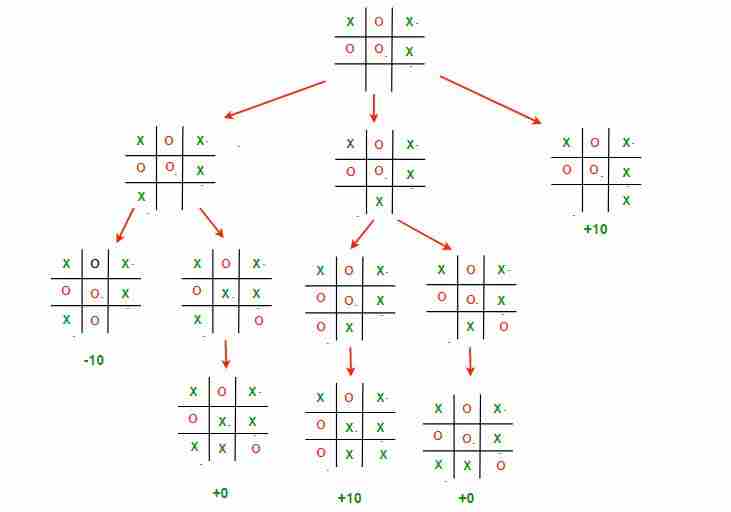
这张图片描绘了游戏从根板状态可以采取的所有可能路径。它通常被称为 博弈树 .
上述示例中的3种可能情况是:
- 左移 :如果X播放[2,0]。然后O将玩[2,1]并赢得比赛。这一步的价值是-10
- 中招 :如果X播放[2,1]。然后O将玩[2,2],这将吸引游戏。此移动的值为0
- 右转 :如果X播放[2,2]。然后他会赢这场比赛。这个移动的值是+10;
请记住,即使X有可能赢,如果他打中间的移动,O将永远不会让这种情况发生,而是会选择抽签。 因此,X的最佳选择是打[2,2],这将保证他获胜。 我们确实鼓励读者尝试提供各种输入,并理解人工智能为什么选择玩这个动作。Minimax可能会让程序员感到困惑,因为它会提前考虑好几步,有时很难调试。请记住,这个minimax算法的实现可以应用于任何两人棋盘游戏,只需对棋盘结构和移动方式进行一些微小的更改。有时,对于像国际象棋这样的复杂游戏,minimax不可能计算出每一种可能的游戏状态。因此,我们只计算到一定深度,并使用评估函数来计算电路板的值。 请继续关注下周我们将讨论的文章 α-β修剪 这可以极大地提高极小极大遍历博弈树所需的时间。
本文由 阿克谢阿拉迪亚酒店 .如果你喜欢GeekSforgek,并想贡献自己的力量,你也可以使用 写极客。组织 或者把你的文章寄去评论-team@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上,并帮助其他极客。 如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写下评论。


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



