极小极大是一种 回溯 一种算法,用于决策和博弈论中,假设你的对手也在最佳状态下,为玩家找到最佳移动。它广泛应用于基于两人回合的游戏,如井字游戏、双陆棋、曼卡拉、国际象棋等。 在Minimax中,这两个参和者被称为最大化者和最小化者。这个 最大化器 努力获得尽可能高的分数,而 最小化 试着做相反的事情,得到尽可能低的分数。 每个董事会状态都有一个与之关联的值。在一个给定的状态下,如果最大化者占上风,那么董事会的分数将趋于某个正值。如果最小值在板状态中占上风,那么它将趋于负值。棋盘的值是通过一些启发式算法计算出来的,这些启发式算法对于每种类型的游戏都是唯一的。
例子: 考虑一个游戏,它有4个最终状态,到达最终状态的路径是从一个完美二叉树的根到4叶,如下所示。假设你是最大化的玩家,你有第一次移动的机会,也就是说,你在根,你的对手在下一个级别。 考虑到你的对手也能发挥最佳水平,作为一名最大化的球员,你会采取哪一步?

由于这是一个基于回溯的算法,它会尝试所有可能的移动,然后回溯并做出决定。
- 最大化者向左:现在是最小化者转向。最小值现在可以在3和5之间选择。作为最小值,它肯定会在两者中选择最小值,即3
- 最大化者右转:现在轮到最小化者了。最小值现在可以在2和9之间选择。他会选择2,因为它是两个值中最小的。
作为最大化者,你会选择更大的值,即3。因此,最大化器的最佳移动是向左移动,最佳值为3。
现在,游戏树如下所示:
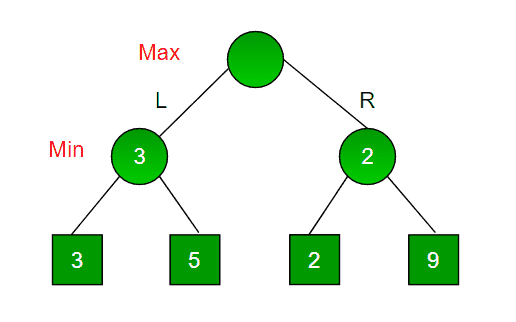
当maximizer向左和向右移动时,上面的树显示了两个可能的分数。
注意:即使右边的子树上有一个值9,最小值也不会选择它。我们必须始终假定我们的对手打得最好。
下面是同样的实现。
C++
// A simple C++ program to find // maximum score that // maximizing player can get. #include<bits/stdc++.h> using namespace std; // Returns the optimal value a maximizer can obtain. // depth is current depth in game tree. // nodeIndex is index of current node in scores[]. // isMax is true if current move is // of maximizer, else false // scores[] stores leaves of Game tree. // h is maximum height of Game tree int minimax( int depth, int nodeIndex, bool isMax, int scores[], int h) { // Terminating condition. i.e // leaf node is reached if (depth == h) return scores[nodeIndex]; // If current move is maximizer, // find the maximum attainable // value if (isMax) return max(minimax(depth+1, nodeIndex*2, false , scores, h), minimax(depth+1, nodeIndex*2 + 1, false , scores, h)); // Else (If current move is Minimizer), find the minimum // attainable value else return min(minimax(depth+1, nodeIndex*2, true , scores, h), minimax(depth+1, nodeIndex*2 + 1, true , scores, h)); } // A utility function to find Log n in base 2 int log2( int n) { return (n==1)? 0 : 1 + log2(n/2); } // Driver code int main() { // The number of elements in scores must be // a power of 2. int scores[] = {3, 5, 2, 9, 12, 5, 23, 23}; int n = sizeof (scores)/ sizeof (scores[0]); int h = log2(n); int res = minimax(0, 0, true , scores, h); cout << "The optimal value is : " << res << endl; return 0; } |
JAVA
// A simple java program to find maximum score that // maximizing player can get. import java.io.*; class GFG { // Returns the optimal value a maximizer can obtain. // depth is current depth in game tree. // nodeIndex is index of current node in scores[]. // isMax is true if current move is of maximizer, else false // scores[] stores leaves of Game tree. // h is maximum height of Game tree static int minimax( int depth, int nodeIndex, boolean isMax, int scores[], int h) { // Terminating condition. i.e leaf node is reached if (depth == h) return scores[nodeIndex]; // If current move is maximizer, find the maximum attainable // value if (isMax) return Math.max(minimax(depth+ 1 , nodeIndex* 2 , false , scores, h), minimax(depth+ 1 , nodeIndex* 2 + 1 , false , scores, h)); // Else (If current move is Minimizer), find the minimum // attainable value else return Math.min(minimax(depth+ 1 , nodeIndex* 2 , true , scores, h), minimax(depth+ 1 , nodeIndex* 2 + 1 , true , scores, h)); } // A utility function to find Log n in base 2 static int log2( int n) { return (n== 1 )? 0 : 1 + log2(n/ 2 ); } // Driver code public static void main (String[] args) { // The number of elements in scores must be // a power of 2. int scores[] = { 3 , 5 , 2 , 9 , 12 , 5 , 23 , 23 }; int n = scores.length; int h = log2(n); int res = minimax( 0 , 0 , true , scores, h); System.out.println( "The optimal value is : " +res); } } // This code is contributed by vt_m |
C#
// A simple C# program to find maximum score that // maximizing player can get. using System; public class GFG { // Returns the optimal value a maximizer can obtain. // depth is current depth in game tree. // nodeIndex is index of current node in scores[]. // isMax is true if current move is of maximizer, else false // scores[] stores leaves of Game tree. // h is maximum height of Game tree static int minimax( int depth, int nodeIndex, bool isMax, int []scores, int h) { // Terminating condition. i.e leaf node is reached if (depth == h) return scores[nodeIndex]; // If current move is maximizer, find the maximum attainable // value if (isMax) return Math.Max(minimax(depth+1, nodeIndex*2, false , scores, h), minimax(depth+1, nodeIndex*2 + 1, false , scores, h)); // Else (If current move is Minimizer), find the minimum // attainable value else return Math.Min(minimax(depth+1, nodeIndex*2, true , scores, h), minimax(depth+1, nodeIndex*2 + 1, true , scores, h)); } // A utility function to find Log n in base 2 static int log2( int n) { return (n==1)? 0 : 1 + log2(n/2); } // Driver code static public void Main () { // The number of elements in scores must be // a power of 2. int []scores = {3, 5, 2, 9, 12, 5, 23, 23}; int n = scores.Length; int h = log2(n); int res = minimax(0, 0, true , scores, h); Console.WriteLine( "The optimal value is : " +res); } } // This code is contributed by ajit. |
Python3
# A simple Python3 program to find # maximum score that # maximizing player can get import math def minimax (curDepth, nodeIndex, maxTurn, scores, targetDepth): # base case : targetDepth reached if (curDepth = = targetDepth): return scores[nodeIndex] if (maxTurn): return max (minimax(curDepth + 1 , nodeIndex * 2 , False , scores, targetDepth), minimax(curDepth + 1 , nodeIndex * 2 + 1 , False , scores, targetDepth)) else : return min (minimax(curDepth + 1 , nodeIndex * 2 , True , scores, targetDepth), minimax(curDepth + 1 , nodeIndex * 2 + 1 , True , scores, targetDepth)) # Driver code scores = [ 3 , 5 , 2 , 9 , 12 , 5 , 23 , 23 ] treeDepth = math.log( len (scores), 2 ) print ( "The optimal value is : " , end = "") print (minimax( 0 , 0 , True , scores, treeDepth)) # This code is contributed # by rootshadow |
Javascript
<script> // Javascript program to find maximum score that // maximizing player can get. // Returns the optimal value a maximizer can obtain. // depth is current depth in game tree. // nodeIndex is index of current node in scores[]. // isMax is true if current move is of maximizer, else false // scores[] stores leaves of Game tree. // h is maximum height of Game tree function minimax(depth, nodeIndex, isMax, scores, h) { // Terminating condition. i.e leaf node is reached if (depth == h) return scores[nodeIndex]; // If current move is maximizer, find the maximum attainable // value if (isMax) return Math.max(minimax(depth+1, nodeIndex*2, false , scores, h), minimax(depth+1, nodeIndex*2 + 1, false , scores, h)); // Else (If current move is Minimizer), find the minimum // attainable value else return Math.min(minimax(depth+1, nodeIndex*2, true , scores, h), minimax(depth+1, nodeIndex*2 + 1, true , scores, h)); } // A utility function to find Log n in base 2 function log2(n) { return (n==1)? 0 : 1 + log2(n/2); } // Driver Code // The number of elements in scores must be // a power of 2. let scores = [3, 5, 2, 9, 12, 5, 23, 23]; let n = scores.length; let h = log2(n); let res = minimax(0, 0, true , scores, h); document.write( "The optimal value is : " +res); </script> |
输出:
The optimal value is: 12
本文的目的是通过一个简单的例子介绍Minimax。
- 在上面的例子中,玩家只有两种选择。总的来说,可以有更多的选择。在这种情况下,我们需要重复所有可能的移动,并找到最大值/最小值。例如,在Tic-Tac-Toe中,第一个玩家可以做出9个可能的动作。
- 在上面的例子中,分数(博弈树的叶子)被提供给我们。对于一个典型的游戏,我们需要导出这些值
我们很快就会用极小极大算法来覆盖Tic-Tac-Toe。 本文由 Akshay L.Aradhya。 如果你喜欢GeekSforgeks,并且想贡献自己的力量,你也可以写一篇文章,然后把你的文章邮寄给评论-team@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上,并帮助其他极客。 如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写评论


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



