欧拉惯性函数 输入n的Φ(n)是{1,2,3,…,n}中与n相对素数的数的计数,即其GCD(最大公约数)与n为1的数。
null
例如,Φ(4)=2,Φ(3)=2和Φ(5)=4。有两个小于或等于4的数字相对素数为4,两个小于或等于3的数字相对素数为3。和4个小于或等于5的数字,它们相对素数为5。 我们已经讨论了不同的计算Φ(n)的方法 以前的职位 .
如何计算所有小于或等于n的数字的Φ?
例子:
Input: n = 5
Output: Totient of 1 is 1
Totient of 2 is 1
Totient of 3 is 2
Totient of 4 is 2
Totient of 5 is 4
我们强烈建议您尽量减少浏览器,并先自己尝试。 A. 简单解决方案 就是打电话 Φ(一) 对于i=1到n。
一 有效解决方案 就是使用一个类似于 埃拉托斯坦筛 预计算所有值。该方法基于以下乘积公式。
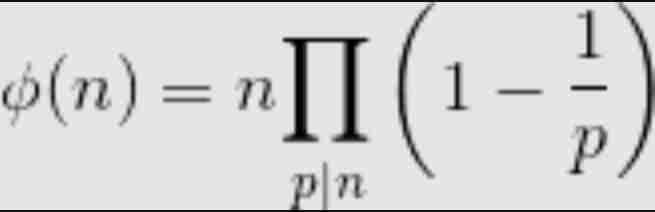
该公式基本上表示,对于n的所有素数p,Φ(n)的值等于n乘以(1-1/p)的乘积。例如Φ(6)=6*(1-1/2)*(1-1/3)=2。
以下是完整的算法:
1) Create an array phi[1..n] to store Φ values of all numbers
from 1 to n.
2) Initialize all values such that phi[i] stores i. This
initialization serves two purposes.
a) To check if phi[i] is already evaluated or not. Note that
the maximum possible phi value of a number i is i-1.
b) To initialize phi[i] as i is multiple in the above product
formula.
3) Run a loop for p = 2 to n
a) If phi[p] is p, means p is not evaluated yet and p is a
prime number (similar to Sieve), otherwise phi[p] must
have been updated in step 3.b
b) Traverse through all multiples of p and update all
multiples of p by multiplying with (1-1/p).
4) Run a loop from i = 1 to n and print all Ph[i] values.
下面是上述算法的实现。
C++
// C++ program to compute Totient function for // all numbers smaller than or equal to n. #include<iostream> using namespace std; // Computes and prints totient of all numbers // smaller than or equal to n. void computeTotient( int n) { // Create and initialize an array to store // phi or totient values long long phi[n+1]; for ( int i=1; i<=n; i++) phi[i] = i; // indicates not evaluated yet // and initializes for product // formula. // Compute other Phi values for ( int p=2; p<=n; p++) { // If phi[p] is not computed already, // then number p is prime if (phi[p] == p) { // Phi of a prime number p is // always equal to p-1. phi[p] = p-1; // Update phi values of all // multiples of p for ( int i = 2*p; i<=n; i += p) { // Add contribution of p to its // multiple i by multiplying with // (1 - 1/p) phi[i] = (phi[i]/p) * (p-1); } } } // Print precomputed phi values for ( int i=1; i<=n; i++) cout << "Totient of " << i << " is " << phi[i] << endl; } // Driver program to test above function int main() { int n = 12; computeTotient(n); return 0; } |
JAVA
// Java program to compute Totient // function for all numbers smaller // than or equal to n. import java.util.*; class GFG { // Computes and prints totient of all numbers // smaller than or equal to n. static void computeTotient( int n) { // Create and initialize an array to store // phi or totient values long phi[] = new long [n + 1 ]; for ( int i = 1 ; i <= n; i++) phi[i] = i; // indicates not evaluated yet // and initializes for product // formula. // Compute other Phi values for ( int p = 2 ; p <= n; p++) { // If phi[p] is not computed already, // then number p is prime if (phi[p] == p) { // Phi of a prime number p is // always equal to p-1. phi[p] = p - 1 ; // Update phi values of all // multiples of p for ( int i = 2 * p; i <= n; i += p) { // Add contribution of p to its // multiple i by multiplying with // (1 - 1/p) phi[i] = (phi[i] / p) * (p - 1 ); } } } // Print precomputed phi values for ( int i = 1 ; i <= n; i++) System.out.println( "Totient of " + i + " is " + phi[i]); } // Driver code public static void main(String[] args) { int n = 12 ; computeTotient(n); } } // This code is contributed by Anant Agarwal. |
Python3
# Python program to compute # Totient function for # all numbers smaller than # or equal to n. # Computes and prints # totient of all numbers # smaller than or equal to n. def computeTotient(n): # Create and initialize # an array to store # phi or totient values phi = [] for i in range (n + 2 ): phi.append( 0 ) for i in range ( 1 , n + 1 ): phi[i] = i # indicates not evaluated yet # and initializes for product # formula. # Compute other Phi values for p in range ( 2 ,n + 1 ): # If phi[p] is not computed already, # then number p is prime if (phi[p] = = p): # Phi of a prime number p is # always equal to p-1. phi[p] = p - 1 # Update phi values of all # multiples of p for i in range ( 2 * p,n + 1 ,p): # Add contribution of p to its # multiple i by multiplying with # (1 - 1/p) phi[i] = (phi[i] / / p) * (p - 1 ) # Print precomputed phi values for i in range ( 1 ,n + 1 ): print ( "Totient of " , i , " is " , phi[i]) # Driver code n = 12 computeTotient(n) # This code is contributed # by Anant Agarwal |
C#
// C# program to check if given two // strings are at distance one. using System; class GFG { // Computes and prints totient of all // numbers smaller than or equal to n static void computeTotient( int n) { // Create and initialize an array to // store phi or totient values long []phi = new long [n + 1]; for ( int i = 1; i <= n; i++) // indicates not evaluated yet // and initializes for product // formula. phi[i] = i; // Compute other Phi values for ( int p = 2; p <= n; p++) { // If phi[p] is not computed already, // then number p is prime if (phi[p] == p) { // Phi of a prime number p is // always equal to p-1. phi[p] = p - 1; // Update phi values of all // multiples of p for ( int i = 2 * p; i <= n; i += p) { // Add contribution of p to its // multiple i by multiplying with // (1 - 1/p) phi[i] = (phi[i] / p) * (p - 1); } } } // Print precomputed phi values for ( int i = 1; i <= n; i++) Console.WriteLine( "Totient of " + i + " is " + phi[i]); } // Driver code public static void Main() { int n = 12; computeTotient(n); } } // This code is contributed by Sam007. |
PHP
<?php // PHP program to compute Totient // function for all numbers smaller // than or equal to n. // Computes and prints totient // of all numbers smaller than // or equal to n. function computeTotient( $n ) { // Create and initialize // an array to store // phi or totient values for ( $i = 1; $i <= $n ; $i ++) // indicates not evaluated yet // and initializes for product // formula. $phi [ $i ] = $i ; // Compute other Phi values for ( $p = 2; $p <= $n ; $p ++) { // If phi[p] is not computed already, // then number p is prime if ( $phi [ $p ] == $p ) { // Phi of a prime number p is // always equal to p-1. $phi [ $p ] = $p - 1; // Update phi values of all // multiples of p for ( $i = 2 * $p ; $i <= $n ; $i += $p ) { // Add contribution of p to its // multiple i by multiplying with // (1 - 1/$p) $phi [ $i ] = ( $phi [ $i ] / $p ) * ( $p - 1); } } } // Print precomputed phi values for ( $i = 1; $i <= $n ; $i ++) echo "Totient of " , $i , " is " , $phi [ $i ] , "" ; } // Driver Code $n = 12; computeTotient( $n ); // This code is contributed by ajit ?> |
Javascript
<script> // Javascript program to check if given two // strings are at distance one. // Computes and prints totient of all // numbers smaller than or equal to n function computeTotient(n) { // Create and initialize an array to // store phi or totient values let phi = new Array(n + 1); for (let i = 1; i <= n; i++) // indicates not evaluated yet // and initializes for product // formula. phi[i] = i; // Compute other Phi values for (let p = 2; p <= n; p++) { // If phi[p] is not computed already, // then number p is prime if (phi[p] == p) { // Phi of a prime number p is // always equal to p-1. phi[p] = p - 1; // Update phi values of all // multiples of p for (let i = 2 * p; i <= n; i += p) { // Add contribution of p to its // multiple i by multiplying with // (1 - 1/p) phi[i] = parseInt(phi[i] / p, 10) * (p - 1); } } } // Print precomputed phi values for (let i = 1; i <= n; i++) document.write( "Totient of " + i + " is " + phi[i] + "</br>" ); } let n = 12; computeTotient(n); </script> |
输出
Totient of 1 is 1 Totient of 2 is 1 Totient of 3 is 2 Totient of 4 is 2 Totient of 5 is 4 Totient of 6 is 2 Totient of 7 is 6 Totient of 8 is 4 Totient of 9 is 6 Totient of 10 is 4 Totient of 11 is 10 Totient of 12 is 4
当我们有大量查询来计算ToClient函数时,也可以使用相同的解决方案。
另一种计算方法 欧拉惯性函数 也可以使用以下公式进行计算:
![图片[2]-所有小于或等于n的数的Euler Toticent函数-yiteyi-C++库](https://www.yiteyi.com/wp-content/uploads/geeks/20210425/geeks_Eulertotientfunction-300x85.png)
欧拉惯性函数
让我们看一个例子来理解上述功能,基本上,它做相同的工作,但方式不同:
例如,ν(12)={(2^(2-1))x(2-1)}x{(3^(1-1))x(3-1)}=4
注意,ψ(n)=n−如果n是素数。
以下是上述公式的实施:
C++
// C++ program for the above approach #include <bits/stdc++.h> using namespace std; #define ll long long ll Euler_totient_function(ll n) { ll result = 1; for (ll i = 2; i * i <= n; i++) { ll c = 0; if (n % i == 0) { while (n % i == 0) { c++; n /= i; } } if (c > 0) { ll power = (ll) pow (i, c - 1); ll sm = (ll) pow (i, c - 1) * (i - 1); result *= sm; } } if (n > 1) { result *= (n - 1); } return result; } // driver code int main() { for (ll i = 1; i < 13; i++) { cout << "Euler_totient_function(" << i << "): " ; cout << Euler_totient_function(i) << endl; } } #praveeny182 |
JAVA
// Java program for the above approach import java.io.*; class GFG{ static long Euler_totient_function( long n) { long result = 1 ; for ( long i = 2 ; i * i <= n; i++) { long c = 0 ; if (n % i == 0 ) { while (n % i == 0 ) { c++; n /= i; } } if (c > 0 ) { long power = ( long )Math.pow(i, c - 1 ); long sm = ( long )Math.pow(i, c - 1 ) * (i - 1 ); result *= sm; } } if (n > 1 ) { result *= (n - 1 ); } return result; } // Driver code public static void main(String[] args) { for ( long i = 1 ; i < 13 ; i++) { System.out.print( "Euler_totient_function(" + i + "): " ); System.out.println(Euler_totient_function(i)); } } } // This code is contributed by rishavmahato348 |
Python3
# python program for the above approach import math def Euler_totient_function(n): result = 1 for i in range ( 2 ,n + 1 ): c = 0 if n % i = = 0 : while (n % i = = 0 ): c + = 1 n / / = i if (c > 0 ): power = math. pow (i,c - 1 ) m = math. pow (i,c - 1 ) * (i - 1 ) result * = m if (n > 1 ): result * = (n - 1 ) return int (result) for i in range ( 1 , 13 ): print ( "Euler_totient_function(" , i , "): " ,end = "") print (Euler_totient_function(i)) |
C#
// C# program for the above approach using System; class GFG { static long Euler_totient_function( long n) { long result = 1; for ( long i = 2; i * i <= n; i++) { long c = 0; if (n % i == 0) { while (n % i == 0) { c++; n /= i; } } if (c > 0) { long sm = ( long )Math.Pow(i, c - 1) * (i - 1); result *= sm; } } if (n > 1) { result *= (n - 1); } return result; } // Driver code public static void Main() { for ( long i = 1; i < 13; i++) { Console.Write( "Euler_totient_function(" + i + "): " ); Console.WriteLine(Euler_totient_function(i)); } } } // This code is contributed by rishavmahato348 |
Javascript
<script> // Javascript program for the above approach function Euler_totient_function(n) { let result = 1; for (let i = 2; i * i <= n; i++) { let c = 0; if (n % i == 0) { while (n % i == 0) { c++; n = parseInt(n / i); } } if (c > 0) { let power = Math.pow(i, c - 1); let sm = Math.pow(i, c - 1) * (i - 1); result *= sm; } } if (n > 1) { result *= (n - 1); } return result; } // driver code for (let i = 1; i < 13; i++) { document.write( "Euler_totient_function(" + i + "): " ); document.write(Euler_totient_function(i) + "<br>" ); } // This code is contributed by subham348. </script> |
输出
Euler_totient_function(1): 1 Euler_totient_function(2): 1 Euler_totient_function(3): 2 Euler_totient_function(4): 2 Euler_totient_function(5): 4 Euler_totient_function(6): 2 Euler_totient_function(7): 6 Euler_totient_function(8): 4 Euler_totient_function(9): 6 Euler_totient_function(10): 4 Euler_totient_function(11): 10 Euler_totient_function(12): 4
本文由 埃克塔·戈尔 。如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请发表评论
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



