埃拉托斯坦筛-yiteyi-C++库

给定一个数字n，打印出所有小于或等于n的素数。同时也给出n是一个小数字。

null

例子：

输入： n=10 输出： 2 3 5 7

输入： n=20 输出： 2 3 5 7 11 13 17 19

当n小于1000万左右时，Eratosthenes筛是找到所有小于n的素数的最有效方法之一（参考维基 ).

建议：请在“上解决” 实践 “首先，在讨论解决方案之前。

下面是通过Eratosthene方法找到小于或等于给定整数n的所有素数的算法：当算法终止时，列表中所有未标记的数字都是素数。

举例说明：

让我们举一个n=50的例子。所以我们需要打印所有小于或等于50的素数。

我们创建一个从2到50的所有数字的列表。

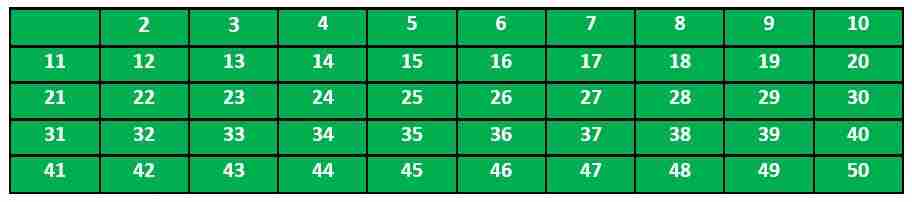
Sieve1

根据该算法，我们将标记所有可被2整除且大于或等于其平方的数字。

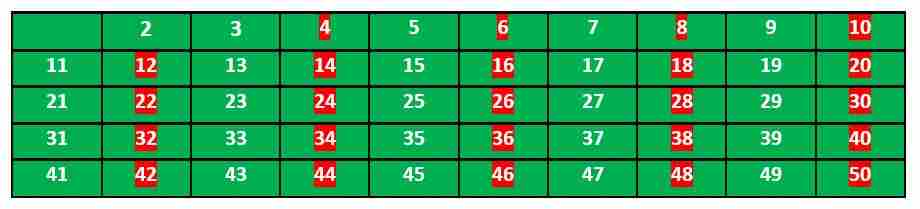
sieve2

现在我们移动到下一个未标记的数字3，标记所有3的倍数，大于或等于其平方的数字。

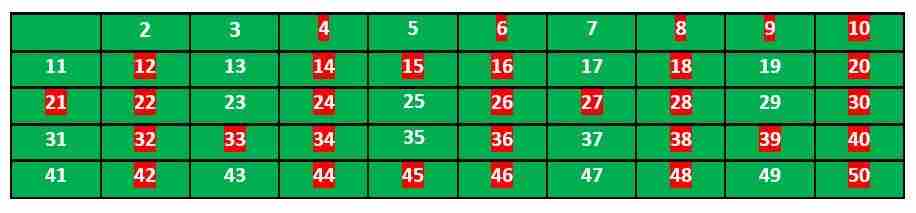
SieveofEratosthenes3

我们移动到下一个未标记的数字5，标记所有大于或等于其平方的5的倍数。

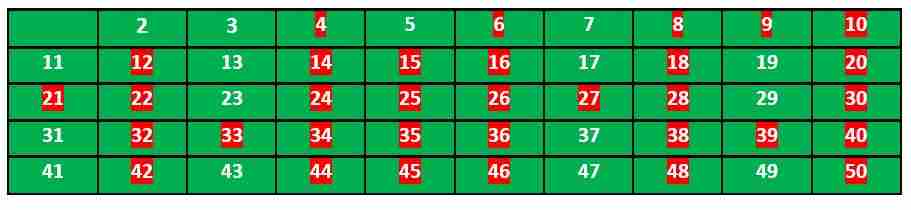
Sieve4

我们继续这个过程，最终的表格如下所示：

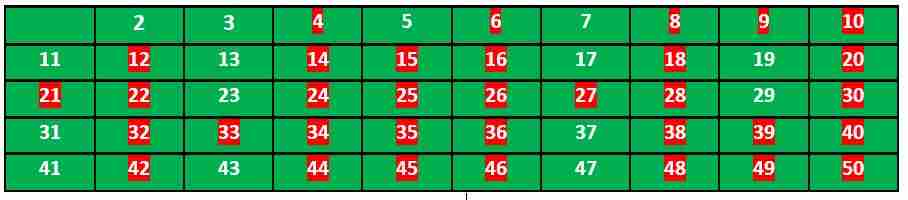
Sieve5

所以素数是没有标记的：2，3，5，7，11，13，17，19，23，29，31，37，41，43，47。

幸亏 克丽珊·库马尔 请提供上述解释。

实施：

下面是上述算法的实现。在下面的实现中，使用大小为n的布尔数组arr[]来标记素数的倍数。

C++

                         // C++ program to print all primes                       
                         // smaller than or equal to                       
                         // n using Sieve of Eratosthenes                       
                         #include <bits/stdc++.h>                       
                         using                                     namespace                                     std;                       
           
                         void                                     SieveOfEratosthenes(                                     int                                     n)                       
                         {                       
                                                 // Create a boolean array                       
                                                 // "prime[0..n]" and initialize                       
                                                 // all entries it as true.                       
                                                 // A value in prime[i] will                       
                                                 // finally be false if i is                       
                                                 // Not a prime, else true.                       
                                                 bool                                     prime[n + 1];                       
                                                 memset                                     (prime,                                     true                                     ,                                     sizeof                                     (prime));                       
           
                                                 for                                     (                                     int                                     p = 2; p * p <= n; p++)                       
                                                 {                       
                                                 // If prime[p] is not changed,                       
                                                 // then it is a prime                       
                                                 if                                     (prime[p] ==                                     true                                     )                       
                                                 {                       
                                                 // Update all multiples                       
                                                 // of p greater than or                       
                                                 // equal to the square of it                       
                                                 // numbers which are multiple                       
                                                 // of p and are less than p^2                       
                                                 // are already been marked.                       
                                                 for                                     (                                     int                                     i = p * p; i <= n; i += p)                       
                                                 prime[i] =                                     false                                     ;                       
                                                 }                       
                                                 }                       
           
                                                 // Print all prime numbers                       
                                                 for                                     (                                     int                                     p = 2; p <= n; p++)                       
                                                 if                                     (prime[p])                       
                                                 cout << p <<                                     " "                                     ;                       
                         }                       
           
                         // Driver Code                       
                         int                                     main()                       
                         {                       
                                                 int                                     n = 30;                       
                                                 cout <<                                     "Following are the prime numbers smaller "                       
                                                 <<                                     " than or equal to "                                     << n << endl;                       
                                                 SieveOfEratosthenes(n);                       
                                                 return                                     0;                       
                         }                       

JAVA

                         // Java program to print all                       
                         // primes smaller than or equal to                       
                         // n using Sieve of Eratosthenes                       
           
                         class                                     SieveOfEratosthenes {                       
                                                 void                                     sieveOfEratosthenes(                                     int                                     n)                       
                                                 {                       
                                                 // Create a boolean array                       
                                                 // "prime[0..n]" and                       
                                                 // initialize all entries                       
                                                 // it as true. A value in                       
                                                 // prime[i] will finally be                       
                                                 // false if i is Not a                       
                                                 // prime, else true.                       
                                                 boolean                                     prime[] =                                     new                                     boolean                                     [n +                                     1                                     ];                       
                                                 for                                     (                                     int                                     i =                                     0                                     ; i <= n; i++)                       
                                                 prime[i] =                                     true                                     ;                       
           
                                                 for                                     (                                     int                                     p =                                     2                                     ; p * p <= n; p++)                       
                                                 {                       
                                                 // If prime[p] is not changed, then it is a                       
                                                 // prime                       
                                                 if                                     (prime[p] ==                                     true                                     )                       
                                                 {                       
                                                 // Update all multiples of p                       
                                                 for                                     (                                     int                                     i = p * p; i <= n; i += p)                       
                                                 prime[i] =                                     false                                     ;                       
                                                 }                       
                                                 }                       
           
                                                 // Print all prime numbers                       
                                                 for                                     (                                     int                                     i =                                     2                                     ; i <= n; i++)                       
                                                 {                       
                                                 if                                     (prime[i] ==                                     true                                     )                       
                                                 System.out.print(i +                                     " "                                     );                       
                                                 }                       
                                                 }                       
           
                                                 // Driver Code                       
                                                 public                                     static                                     void                                     main(String args[])                       
                                                 {                       
                                                 int                                     n =                                     30                                     ;                       
                                                 System.out.print(                       
                                                 "Following are the prime numbers "                                     );                       
                                                 System.out.println(                                     "smaller than or equal to "                                     + n);                       
                                                 SieveOfEratosthenes g =                                     new                                     SieveOfEratosthenes();                       
                                                 g.sieveOfEratosthenes(n);                       
                                                 }                       
                         }                       
           
                         // This code has been contributed by Amit Khandelwal.                       

Python3

                         # Python program to print all                       
                         # primes smaller than or equal to                       
                         # n using Sieve of Eratosthenes                       
           
           
                         def                                     SieveOfEratosthenes(n):                       
           
                                                 # Create a boolean array                       
                                                 # "prime[0..n]" and initialize                       
                                                 #  all entries it as true.                       
                                                 # A value in prime[i] will                       
                                                 # finally be false if i is                       
                                                 # Not a prime, else true.                       
                                                 prime                                     =                                     [                                     True                                     for                                     i                                     in                                     range                                     (n                                     +                                     1                                     )]                       
                                                 p                                     =                                     2                       
                                                 while                                     (p                                     *                                     p <                                     =                                     n):                       
           
                                                 # If prime[p] is not                       
                                                 # changed, then it is a prime                       
                                                 if                                     (prime[p]                                     =                                     =                                     True                                     ):                       
           
                                                 # Update all multiples of p                       
                                                 for                                     i                                     in                                     range                                     (p                                     *                                     p, n                                     +                                     1                                     , p):                       
                                                 prime[i]                                     =                                     False                       
                                                 p                                     +                                     =                                     1                       
           
                                                 # Print all prime numbers                       
                                                 for                                     p                                     in                                     range                                     (                                     2                                     , n                                     +                                     1                                     ):                       
                                                 if                                     prime[p]:                       
                                                 print                                     (p)                       
           
           
                         # Driver code                       
                         if                                     __name__                                     =                                     =                                     '__main__'                                     :                       
                                                 n                                     =                                     20                       
                                                 print                                     (                                     "Following are the prime numbers smaller"                                     ),                       
                                                 print                                     (                                     "than or equal to"                                     , n)                       
                                                 SieveOfEratosthenes(n)                       

C#

                         // C# program to print all primes                       
                         // smaller than or equal to n                       
                         // using Sieve of Eratosthenes                       
                         using                                     System;                       
           
                         namespace                                     prime {                       
                         public                                     class                                     GFG {                       
           
                                                 public                                     static                                     void                                     SieveOfEratosthenes(                                     int                                     n)                       
                                                 {                       
           
                                                 // Create a boolean array                       
                                                 // "prime[0..n]" and                       
                                                 // initialize all entries                       
                                                 // it as true. A value in                       
                                                 // prime[i] will finally be                       
                                                 // false if i is Not a                       
                                                 // prime, else true.                       
           
                                                 bool                                     [] prime =                                     new                                     bool                                     [n + 1];                       
           
                                                 for                                     (                                     int                                     i = 0; i <= n; i++)                       
                                                 prime[i] =                                     true                                     ;                       
           
                                                 for                                     (                                     int                                     p = 2; p * p <= n; p++)                       
                                                 {                       
                                                 // If prime[p] is not changed,                       
                                                 // then it is a prime                       
                                                 if                                     (prime[p] ==                                     true                                     )                       
                                                 {                       
                                                 // Update all multiples of p                       
                                                 for                                     (                                     int                                     i = p * p; i <= n; i += p)                       
                                                 prime[i] =                                     false                                     ;                       
                                                 }                       
                                                 }                       
           
                                                 // Print all prime numbers                       
                                                 for                                     (                                     int                                     i = 2; i <= n; i++)                       
                                                 {                       
                                                 if                                     (prime[i] ==                                     true                                     )                       
                                                 Console.Write(i +                                     " "                                     );                       
                                                 }                       
                                                 }                       
           
                                                 // Driver Code                       
                                                 public                                     static                                     void                                     Main()                       
                                                 {                       
                                                 int                                     n = 30;                       
                                                 Console.WriteLine(                       
                                                 "Following are the prime numbers"                                     );                       
                                                 Console.WriteLine(                                     "smaller than or equal to "                                     + n);                       
                                                 SieveOfEratosthenes(n);                       
                                                 }                       
                         }                       
                         }                       
           
                         // This code is contributed by Sam007.                       

PHP

                         <?php                       
                         // php program to print all primes smaller                       
                         // than or equal to n using Sieve of                       
                         // Eratosthenes                       
           
                         function                                     SieveOfEratosthenes(                                     $n                                     )                       
                         {                       
                                                 // Create a boolean array "prime[0..n]"                       
                                                 // and initialize all entries it as true.                       
                                                 // A value in prime[i] will finally be                       
                                                 // false if i is Not a prime, else true.                       
                                                 $prime                                     =                                     array_fill                                     (0,                                     $n                                     +1, true);                       
           
                                                 for                                     (                                     $p                                     = 2;                                     $p                                     *                                     $p                                     <=                                     $n                                     ;                                     $p                                     ++)                       
                                                 {                       
                                   
                                                 // If prime[p] is not changed,                       
                                                 // then it is a prime                       
                                                 if                                     (                                     $prime                                     [                                     $p                                     ] == true)                       
                                                 {                       
                                   
                                                 // Update all multiples of p                       
                                                 for                                     (                                     $i                                     =                                     $p                                     *                                     $p                                     ;                                     $i                                     <=                                     $n                                     ;                                     $i                                     +=                                     $p                                     )                       
                                                 $prime                                     [                                     $i                                     ] = false;                       
                                                 }                       
                                                 }                       
           
                                                 // Print all prime numbers                       
                                                 for                                     (                                     $p                                     = 2;                                     $p                                     <=                                     $n                                     ;                                     $p                                     ++)                       
                                                 if                                     (                                     $prime                                     [                                     $p                                     ])                       
                                                 echo                                     $p                                     .                                     " "                                     ;                       
                         }                       
           
                         // Driver Code                       
                                                 $n                                     = 30;                       
                                                 echo                                     "Following are the prime numbers "                       
                                                 .                                     "smaller than or equal to "                                     .                                     $n                                     .                                     ""                                     ;                       
                                                 SieveOfEratosthenes(                                     $n                                     );                       
           
                         // This code is contributed by mits                       
                         ?>                       

Javascript

                         <script>                       
           
                         // javascript program to print all                       
                         // primes smaller than or equal to                       
                         // n using Sieve of Eratosthenes                       
           
           
                         function                                     sieveOfEratosthenes(n)                       
                         {                       
                                                 // Create a boolean array                       
                                                 // "prime[0..n]" and                       
                                                 // initialize all entries                       
                                                 // it as true. A value in                       
                                                 // prime[i] will finally be                       
                                                 // false if i is Not a                       
                                                 // prime, else true.                       
                                                 prime = Array.from({length: n+1}, (_, i) =>                                     true                                     );                       
           
                                                 for                                     (p = 2; p * p <= n; p++)                       
                                                 {                       
                                                 // If prime[p] is not changed, then it is a                       
                                                 // prime                       
                                                 if                                     (prime[p] ==                                     true                                     )                       
                                                 {                       
                                                 // Update all multiples of p                       
                                                 for                                     (i = p * p; i <= n; i += p)                       
                                                 prime[i] =                                     false                                     ;                       
                                                 }                       
                                                 }                       
           
                                                 // Print all prime numbers                       
                                                 for                                     (i = 2; i <= n; i++)                       
                                                 {                       
                                                 if                                     (prime[i] ==                                     true                                     )                       
                                                 document.write(i +                                     " "                                     );                       
                                                 }                       
                         }                       
           
                         // Driver Code                       
                         var                                     n = 30;                       
                         document.write(                       
                                                 "Following are the prime numbers "                                     );                       
                         document.write(                                     "smaller than or equal to "                                     + n+                                     "<br>"                                     );                       
                         sieveOfEratosthenes(n);                       
           
                         // This code is contributed by 29AjayKumar                       
           
                         </script>                       

时间复杂性： O（n*log（log（n）））

辅助空间： O（n）

C++

                         // the following implementation                       
                         // stores only halves of odd numbers                       
                         // the algorithm is a faster by some constant factors                       
           
                         #include <bitset>                       
                         #include <iostream>                       
                         using                                     namespace                                     std;                       
           
                         bitset<500001> Primes;                       
                         void                                     SieveOfEratosthenes(                                     int                                     n)                       
                         {                       
                                                 Primes[0] = 1;                       
                                                 for                                     (                                     int                                     i = 3; i <= n; i += 2) {                       
                                                 if                                     (Primes[i / 2] == 0) {                       
                                                 for                                     (                                     int                                     j = 3 * i; j <= n; j += 2 * i)                       
                                                 Primes[j / 2] = 1;                       
                                                 }                       
                                                 }                       
                         }                       
           
                         int                                     main()                       
                         {                       
                                                 int                                     n = 100;                       
                                                 SieveOfEratosthenes(n);                       
                                                 for                                     (                                     int                                     i = 1; i <= n; i++) {                       
                                                 if                                     (i == 2)                       
                                                 cout << i <<                                     ' '                                     ;                       
                                                 else                                     if                                     (i % 2 == 1 && Primes[i / 2] == 0)                       
                                                 cout << i <<                                     ' '                                     ;                       
                                                 }                       
                                                 return                                     0;                       
                         }                       

C#

                         // C# program for the above approach                       
                         using                                     System;                       
                         public                                     class                                     GFG {                       
           
                                                 static                                     int                                     [] Primes =                                     new                                     int                                     [500001];                       
           
                                                 static                                     void                                     SieveOfEratosthenes(                                     int                                     n)                       
                                                 {                       
                                                 Primes[0] = 1;                       
                                                 for                                     (                                     int                                     i = 3; i <= n; i += 2) {                       
                                                 if                                     (Primes[i / 2] == 0) {                       
                                                 for                                     (                                     int                                     j = 3 * i; j <= n; j += 2 * i)                       
                                                 Primes[j / 2] = 1;                       
                                                 }                       
                                                 }                       
                                                 }                       
           
                                                 // Driver Code                       
                                                 public                                     static                                     void                                     Main(String[] args) {                       
           
                                                 int                                     n = 100;                       
                                                 SieveOfEratosthenes(n);                       
                                                 for                                     (                                     int                                     i = 1; i <= n; i++) {                       
                                                 if                                     (i == 2)                       
                                                 Console.Write(i +                                     " "                                     );                       
                                                 else                                     if                                     (i % 2 == 1 && Primes[i / 2] == 0)                       
                                                 Console.Write(i +                                     " "                                     );                       
                                                 }                       
                                                 }                       
                         }                       
           
                         // This code is contributed by sanjoy_62.                       

您可能还想看到：

文章版权归作者所有，未经允许请勿转载。

THE END

技术文章