条件概率 条件概率P(A | B)表示偶数“A”发生的概率,假设偶数“B”发生。
![]()
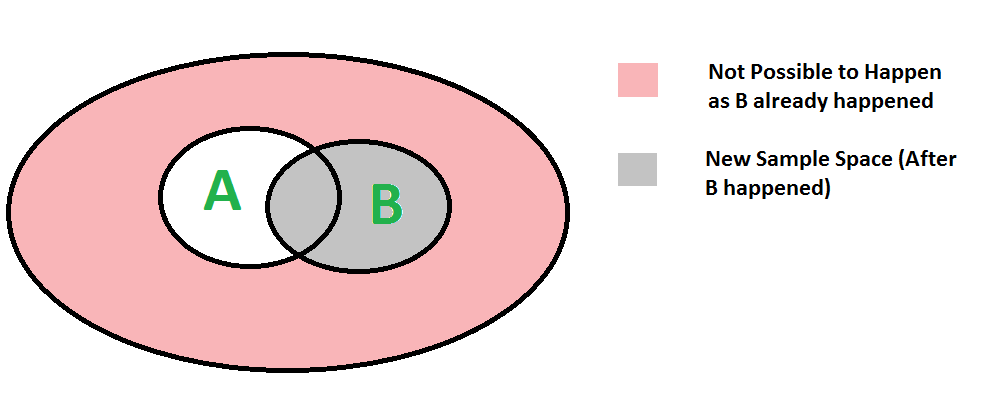
我们可以用下面的图表很容易地理解上面的公式。由于B已经发生,样本空间减少到B,所以A发生的概率变成P(A)∩ B) 除以P(B)
下面是 贝叶斯公式 条件概率。
![]()
该公式提供了P(A | B)和P(B | A)之间的关系。它主要由文中讨论的条件概率公式导出 以前的职位 .
考虑下面的条件概率公式p(a,b)和p(b a)
![]()
![]()
自P(B)∩ A) =P(A)∩ B) 我们可以替换∩ B) 在第一个公式中,P(B | A)P(A) 替换后,我们得到给定的公式。指代 这 例如贝叶斯公式。
随机变量: 随机变量实际上是一个将随机事件(如抛硬币)的结果映射到实际值的函数。
例子:
Coin tossing game : A player pays 50 bucks if result of cointoss is "Head" The person gets 50 bucks if the result isTail. A random variable profit for person can be defined as below : Profit = +50 if Head -50 if Tail Generally gambling games are not fair for players, the organizer takes a share of profit for all arrangements. So expected profit is negative for a player in gambling and positive for the organizer. That is how organizers make money.
随机变量的期望值: 随机变量R的期望值可定义如下
E[R] = r1*p1 + r2*p2 + ... rk*pk ri ==> Value of R with probability pi
期望值基本上是以下两项的乘积之和(对于所有可能的事件) a) 事件发生的概率。 b) 在那个偶数下R的值
Example 1:In above example of coin toss,Expected value of profit = 50 * (1/2) + (-50) * (1/2) = 0Example 2:Expected value of six faced dice throw is = 1*(1/6) + 2*(1/6) + .... + 6*(1/6) = 3.5
期望线性: 让R 1. 和R 2. 是某个概率空间上的两个离散随机变量
E[R1 + R2] = E[R1] + E[R2]
例如,3次掷骰子的总和预期值为=3*7/2=7
参考 这 以获取更详细的解释和示例。
成功前的预期试验次数 如果在每一次试验中成功的概率是P,那么预期的试验次数直到成功率为1/P。例如,考虑6面公平骰子被抛到“5”被视为掷骰子的结果。在看到5之前的预期投掷次数是6。请注意,1/6是每次试验得5分的概率。所以试验的数量是1/(1/6)=6。 作为另一个例子,考虑一个QuestRoad版本,它一直在寻找枢轴直到一个中间N/2个元素被选中。寻找中间支点的预期试验次数为2次,因为选择中间n/2元素之一的概率为1/2。本示例将在中进行更详细的讨论 第一组 . 参考 这 以获取更详细的解释和示例。
更多关于随机算法的信息:
本文由 希瓦姆·古普塔 。如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请发表评论
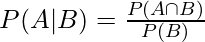


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



