考虑坡度线1在节点之间通过。给定一棵二叉树,打印二叉树中属于同一行的所有对角线元素。
null
Input : Root of below tree
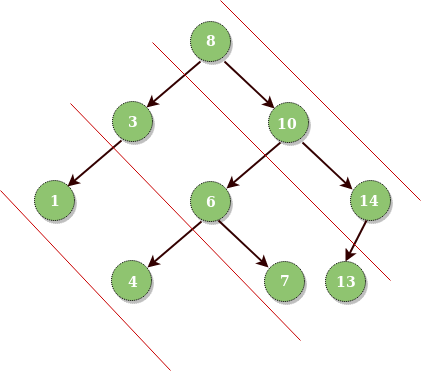
Output : Diagonal Traversal of binary tree : 8 10 14 3 6 7 13 1 4Observation : root and root->right values will be prioritized over all root->left values.
这个想法是使用地图。我们使用不同的坡度距离,并将其用作地图中的关键点。地图中的值是节点的向量(或动态数组)。我们遍历树以在地图中存储值。一旦建立了地图,我们就会打印地图的内容。
下面是上述想法的实施。
C++
// C++ program for diagonal // traversal of Binary Tree #include <bits/stdc++.h> using namespace std; // Tree node struct Node { int data; Node *left, *right; }; /* root - root of the binary tree d - distance of current line from rightmost -topmost slope. diagonalPrint - multimap to store Diagonal elements (Passed by Reference) */ void diagonalPrintUtil(Node* root, int d, map< int , vector< int >> &diagonalPrint) { // Base case if (!root) return ; // Store all nodes of same // line together as a vector diagonalPrint[d].push_back(root->data); // Increase the vertical // distance if left child diagonalPrintUtil(root->left, d + 1, diagonalPrint); // Vertical distance remains // same for right child diagonalPrintUtil(root->right, d, diagonalPrint); } // Print diagonal traversal // of given binary tree void diagonalPrint(Node* root) { // create a map of vectors // to store Diagonal elements map< int , vector< int > > diagonalPrint; diagonalPrintUtil(root, 0, diagonalPrint); cout << "Diagonal Traversal of binary tree : " ; for ( auto it :diagonalPrint) { vector< int > v=it.second; for ( auto it:v) cout<<it<< " " ; cout<<endl; } } // Utility method to create a new node Node* newNode( int data) { Node* node = new Node; node->data = data; node->left = node->right = NULL; return node; } // Driver program int main() { Node* root = newNode(8); root->left = newNode(3); root->right = newNode(10); root->left->left = newNode(1); root->left->right = newNode(6); root->right->right = newNode(14); root->right->right->left = newNode(13); root->left->right->left = newNode(4); root->left->right->right = newNode(7); /* Node* root = newNode(1); root->left = newNode(2); root->right = newNode(3); root->left->left = newNode(9); root->left->right = newNode(6); root->right->left = newNode(4); root->right->right = newNode(5); root->right->left->right = newNode(7); root->right->left->left = newNode(12); root->left->right->left = newNode(11); root->left->left->right = newNode(10);*/ diagonalPrint(root); return 0; } |
JAVA
// Java program for diagonal // traversal of Binary Tree import java.util.TreeMap; import java.util.Map.Entry; import java.util.Vector; public class DiagonalTraversalBTree { // Tree node static class Node { int data; Node left; Node right; //constructor Node( int data) { this .data=data; left = null ; right = null ; } } /* root - root of the binary tree d - distance of current line from rightmost -topmost slope. diagonalPrint - HashMap to store Diagonal elements (Passed by Reference) */ static void diagonalPrintUtil(Node root, int d, TreeMap<Integer,Vector<Integer>> diagonalPrint) { // Base case if (root == null ) return ; // get the list at the particular d value Vector<Integer> k = diagonalPrint.get(d); // k is null then create a // vector and store the data if (k == null ) { k = new Vector<>(); k.add(root.data); } // k is not null then update the list else { k.add(root.data); } // Store all nodes of same line // together as a vector diagonalPrint.put(d,k); // Increase the vertical distance // if left child diagonalPrintUtil(root.left, d + 1 , diagonalPrint); // Vertical distance remains // same for right child diagonalPrintUtil(root.right, d, diagonalPrint); } // Print diagonal traversal // of given binary tree static void diagonalPrint(Node root) { // create a map of vectors // to store Diagonal elements TreeMap<Integer,Vector<Integer>> diagonalPrint = new TreeMap<>(); diagonalPrintUtil(root, 0 , diagonalPrint); System.out.println( "Diagonal Traversal of Binary Tree" ); for (Entry<Integer, Vector<Integer>> entry : diagonalPrint.entrySet()) { System.out.println(entry.getValue()); } } // Driver program public static void main(String[] args) { Node root = new Node( 8 ); root.left = new Node( 3 ); root.right = new Node( 10 ); root.left.left = new Node( 1 ); root.left.right = new Node( 6 ); root.right.right = new Node( 14 ); root.right.right.left = new Node( 13 ); root.left.right.left = new Node( 4 ); root.left.right.right = new Node( 7 ); diagonalPrint(root); } } // This code is contributed by Sumit Ghosh |
Python3
# Python program for diagonal # traversal of Binary Tree # A binary tree node class Node: # Constructor to create a # new binary tree node def __init__( self , data): self .data = data self .left = None self .right = None """ root - root of the binary tree d - distance of current line from rightmost -topmost slope. diagonalPrint - multimap to store Diagonal elements (Passed by Reference) """ def diagonalPrintUtil(root, d, diagonalPrintMap): # Base Case if root is None : return # Store all nodes of same line # together as a vector try : diagonalPrintMap[d].append(root.data) except KeyError: diagonalPrintMap[d] = [root.data] # Increase the vertical distance # if left child diagonalPrintUtil(root.left, d + 1 , diagonalPrintMap) # Vertical distance remains # same for right child diagonalPrintUtil(root.right, d, diagonalPrintMap) # Print diagonal traversal of given binary tree def diagonalPrint(root): # Create a dict to store diagonal elements diagonalPrintMap = dict () # Find the diagonal traversal diagonalPrintUtil(root, 0 , diagonalPrintMap) print ( "Diagonal Traversal of binary tree : " ) for i in diagonalPrintMap: for j in diagonalPrintMap[i]: print (j,end = " " ) print () # Driver Program root = Node( 8 ) root.left = Node( 3 ) root.right = Node( 10 ) root.left.left = Node( 1 ) root.left.right = Node( 6 ) root.right.right = Node( 14 ) root.right.right.left = Node( 13 ) root.left.right.left = Node( 4 ) root.left.right.right = Node( 7 ) diagonalPrint(root) # This code is contributed by Nikhil Kumar Singh(nickzuck_007) |
输出
Diagonal Traversal of binary tree : 8 10 14 3 6 7 13 1 4
这个 时间复杂性 这个解决方案的关键是 O(N logN) 空间的复杂性是 O(N)
我们可以使用队列和迭代算法来解决同样的问题。
Python3
from collections import deque # A binary tree node class Node: # Constructor to create a # new binary tree node def __init__( self , data): self .data = data self .left = None self .right = None def diagonal(root): out = [] node = root # queue to store left nodes left_q = deque() while node: # append data to output array out.append(node.data) # if left available add it to the queue if node.left: left_q.appendleft(node.left) # if right is available change the node if node.right: node = node.right else : # else pop the left_q if len (left_q) > = 1 : node = left_q.pop() else : node = None return out # Driver Code root = Node( 8 ) root.left = Node( 3 ) root.right = Node( 10 ) root.left.left = Node( 1 ) root.left.right = Node( 6 ) root.right.right = Node( 14 ) root.right.right.left = Node( 13 ) root.left.right.left = Node( 4 ) root.left.right.right = Node( 7 ) print (diagonal(root)) |
C++14
#include <bits/stdc++.h> using namespace std; // Tree node struct Node { int data; Node *left, *right; }; vector< int > diagonal(Node* root) { vector< int > diagonalVals; if (!root) return diagonalVals; // The leftQueue will be a queue which will store all // left pointers while traversing the tree, and will be // utilized when at any point right pointer becomes NULL queue<Node*> leftQueue; Node* node = root; while (node) { // Add current node to output diagonalVals.push_back(node->data); // If left child available, add it to queue if (node->left) leftQueue.push(node->left); // if right child, transfer the node to right if (node->right) node = node->right; else { // If left child Queue is not empty, utilize it // to traverse further if (!leftQueue.empty()) { node = leftQueue.front(); leftQueue.pop(); } else { // All the right childs traversed and no // left child left node = NULL; } } } return diagonalVals; } // Utility method to create a new node Node* newNode( int data) { Node* node = new Node; node->data = data; node->left = node->right = NULL; return node; } // Driver program int main() { Node* root = newNode(8); root->left = newNode(3); root->right = newNode(10); root->left->left = newNode(1); root->left->right = newNode(6); root->right->right = newNode(14); root->right->right->left = newNode(13); root->left->right->left = newNode(4); root->left->right->right = newNode(7); /* Node* root = newNode(1); root->left = newNode(2); root->right = newNode(3); root->left->left = newNode(9); root->left->right = newNode(6); root->right->left = newNode(4); root->right->right = newNode(5); root->right->left->right = newNode(7); root->right->left->left = newNode(12); root->left->right->left = newNode(11); root->left->left->right = newNode(10);*/ vector< int > diagonalValues = diagonal(root); for ( int i = 0; i < diagonalValues.size(); i++) { cout << diagonalValues[i] << " " ; } cout << endl; return 0; } |
输出
[8, 10, 14, 3, 6, 7, 13, 1, 4]
这个 时间复杂性 这个解决方案的关键是 O(N logN) 空间的复杂性是 O(N)
方法2:使用队列。
每个节点都有助于生成下一条对角线。只有当元素的左边可用时,我们才会将其推送到队列中。我们将处理节点并移到其右侧。
代码:
C++
#include <bits/stdc++.h> using namespace std; struct Node { int data; Node *left, *right; }; Node* newNode( int data) { Node* node = new Node; node->data = data; node->left = node->right = NULL; return node; } vector <vector < int >> result; void diagonalPrint(Node* root) { if (root == NULL) return ; queue <Node*> q; q.push(root); while (!q.empty()) { int size = q.size(); vector < int > answer; while (size--) { Node* temp = q.front(); q.pop(); // traversing each component; while (temp) { answer.push_back(temp->data); if (temp->left) q.push(temp->left); temp = temp->right; } } result.push_back(answer); } } int main() { Node* root = newNode(8); root->left = newNode(3); root->right = newNode(10); root->left->left = newNode(1); root->left->right = newNode(6); root->right->right = newNode(14); root->right->right->left = newNode(13); root->left->right->left = newNode(4); root->left->right->right = newNode(7); diagonalPrint(root); for ( int i=0 ; i<result.size() ; i++) { for ( int j=0 ; j<result[i].size() ; j++) cout<<result[i][j]<< " " ; cout<<endl; } return 0; } |
JAVA
import java.io.*; import java.util.*; class GFG{ // Tree node static class Node { int data; Node left; Node right; // Constructor Node( int data) { this .data = data; left = null ; right = null ; } } static class TNode { Node node; int level; public TNode(Node n, int l) { this .node = n; this .level = l; } } public static void diagonalPrint(Node root) { if (root == null ) { return ; } TreeMap<Integer, List<Integer>> map = new TreeMap<Integer, List<Integer>>(); Queue<TNode> q = new LinkedList<TNode>(); q.add( new TNode(root, 0 )); while (!q.isEmpty()) { TNode curr = q.poll(); map.putIfAbsent(curr.level, new ArrayList<>()); map.get(curr.level).add(curr.node.data); if (curr.node.left != null ) { q.add( new TNode(curr.node.left, curr.level + 1 )); } if (curr.node.right != null ) { q.add( new TNode(curr.node.right, curr.level)); } } for (Map.Entry<Integer, List<Integer>> entry : map.entrySet()) { int k = entry.getKey(); List<Integer> l = map.get(k); int size = l.size(); for ( int i = 0 ; i < l.size(); i++) { System.out.print(l.get(i)); System.out.print( " " ); } System.out.println( "" ); } return ; } // Driver code public static void main(String[] args) { Node root = new Node( 8 ); root.left = new Node( 3 ); root.right = new Node( 10 ); root.left.left = new Node( 1 ); root.left.right = new Node( 6 ); root.right.right = new Node( 14 ); root.right.right.left = new Node( 13 ); root.left.right.left = new Node( 4 ); root.left.right.right = new Node( 7 ); diagonalPrint(root); } } // This code is contributed by abhinaygupta98 |
输出
8 10 14 3 6 7 13 1 4
时间复杂度:O(N) ,因为我们只访问一次节点。
空间复杂性:O(N) ,因为我们正在使用队列。
本文由 阿迪蒂亚·戈尔 。如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请发表评论。
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



