随机算法|集合3（1/2近似中值）

我们强烈建议将以下文章作为本课程的先决条件。

随机算法|集1（介绍和分析） 随机算法|集2（分类和应用）

本文讨论了蒙特卡罗算法。

问题陈述： 给定一个n个数且ε>0的未排序数组A[]，计算其秩（在排序的A[]中的位置）在[（1-ε）n/2，（1+ε）n/2]范围内的元素。 对于½近似中值算法&epsilom；is 1/2=>等级应在[n/4，3n/4]范围内

我们可以在图中找到第k个最小元素 O（n）预计时间 和 O（n）最坏情况 时间

如果我们希望在不到O（n）的时间内，允许的概率误差很低，该怎么办？ 以下步骤表示一个算法，该算法为O（（logn）x（logn））时间，并产生概率小于或等于2/n的错误结果 ^2. .

1. 从数组中随机选择k个元素，其中k=c logn（c是某个常数）
2. 然后插入一组。
3. 对集合中的元素进行排序。
4. 返回集合的中位数，即集合中的第（k/2）个元素

   C

   /* C++ program to find Approximate Median using 1/2 Approximate Algorithm */ #include<bits/stdc++.h> using namespace std; // This function returns the Approximate Median int randApproxMedian( int arr[], int n) { // Declaration for the random number generator random_device rand_dev; mt19937 generator(rand_dev()); // Random number generated will be in the range [0,n-1] uniform_int_distribution< int > distribution(0, n-1); if (n==0) return 0; int k = 10*log2(n); // Taking c as 10 // A set stores unique elements in sorted order set< int > s; for ( int i=0; i<k; i++) { // Generating a random index int index = distribution(generator); //Inserting into the set s.insert(arr[index]); } set< int > ::iterator itr = s.begin(); // Report the median of the set at k/2 position // Move the itr to k/2th position advance(itr, (s.size()/2) - 1); // Return the median return *itr; } // Driver method to test above method int main() { int arr[] = {1, 3, 2, 4, 5, 6, 8, 7}; int n = sizeof (arr)/ sizeof ( int ); printf ( "Approximate Median is %d" ,randApproxMedian(arr,n)); return 0 }

   JAVA

   /* Java program to find Approximate Median using 1/2 Approximate Algorithm */ import java.util.Iterator; import java.util.Random; import java.util.TreeSet; class Test { static int arr[] = new int []{ 1 , 3 , 2 , 4 , 5 , 6 , 8 , 7 } ; // This function returns the Approximate Median static int randApproxMedian( int n) { // Declaration for the random number Random r = new Random(); if (n== 0 ) return 0 ; double k1 = 10 *Math.log(n); // Taking c as 10 int k = ( int )k1; // A treeset stores unique elements in sorted order TreeSet s = new TreeSet<Integer>(); for ( int i= 0 ; i<k; i++) { // Generating a random index // Random number generated will be in the range [0,n-1] int index = r.nextInt(n); //Inserting into the set s.add(arr[index]); } Iterator<Integer> itr = s.iterator(); int temp = s.size()/ 2 - 1 ; for ( int i = 0 ; i < temp; i++) { itr.next(); } // Return the median return itr.next(); } // Driver method to test the above function public static void main(String[] args) { System.out.println( "Approximate Median is " + randApproxMedian(arr.length)); } }

   输出：

   Approximate Median is 4

   时间复杂性： 我们使用C++中STL提供的一组。在STL集合中，每个元素的插入都需要O（logk）。所以对于k个插入，所花费的时间是O（k logk）。 现在用c log n替换k =>O（c log n（log（clog n）））=>O（log n（log n））

   错误概率如何小于2/n ^2. ? 如果集合S至少有k/2个元素来自左四分之一或右四分之一，则算法会出错。

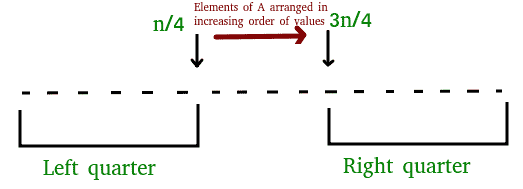
   这句话很容易形象化，因为我们报告的中位数将是第（k/2）个元素，如果我们从左四分之一（或右四分之一）取k/2个元素，中位数将来自左四分之一（或右四分之一）。

   一个阵列可以分为四个四分之一，每个四分之一的大小为n/4。所以P（选择左四分之一）是1/4。那么，至少k/2元素来自左四分之一或右四分之一的概率是多少？这个概率问题如下所示：

   给出一枚硬币，正面概率为1/4，反面概率为3/4。硬币被抛了k次。我们得到至少k/2头小于或等于的概率是多少？

   说明：

   If we put k = c log n for c = 10, we get 
   P <= (1/2)2log n
   P <= (1/2)log n2
   P <= n-2
   

   从左四分之一中选择至少k/2个元素的概率）<=1/n ^2. 从左四分之一或右四分之一中选择至少k/2个元素的概率）<=2/n ^2.

   因此，算法产生的错误结果的概率小于或等于2/n ^2. .

   参考资料： www.cse。iitk。ac.in/users/sbaswana/CS648/TEACH-2-CS648。pptx

   本文由 希拉格·阿加瓦尔 .如果你喜欢GeekSforgek，并且想贡献自己的力量，你也可以写一篇文章，并将文章邮寄到contribute@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上，并帮助其他极客。

   如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请写评论