给定输入文本和k个单词的数组arr[],查找输入文本中所有单词的所有匹配项。允许 N 是文本的长度和 M 是所有单词中的字符总数,即m=长度(arr[0])+长度(arr[1])+…+长度(arr[k-1])。在这里 K 是输入单词的总数。
例子:
Input: text = "ahishers"
arr[] = {"he", "she", "hers", "his"}
Output:
Word his appears from 1 to 3
Word he appears from 4 to 5
Word she appears from 3 to 5
Word hers appears from 4 to 7
如果我们使用线性时间搜索算法,比如 国民党 ,然后我们需要逐个搜索文本[]中的所有单词。这使得我们的总时间复杂度为O(n+length(word[0])+O(n+length(word[1])+O(n+length(word[2])+…O(n+length(word[k-1])。这种时间复杂性可以写成 O(n*k+m) .
Aho-Corasick算法 查找中的所有单词 O(n+m+z) 时间和地点 Z 是文本中出现的单词总数。Aho–Corasick字符串匹配算法构成了原始Unix命令fgrep的基础。
- 预处理: 构建arr[]中所有单词的自动机该自动机主要有三个功能:
Go To : This function simply follows edges
of Trie of all words in arr[]. It is
represented as 2D array g[][] where
we store next state for current state
and character.
Failure : This function stores all edges that are
followed when current character doesn't
have edge in Trie. It is represented as
1D array f[] where we store next state for
current state.
Output : Stores indexes of all words that end at
current state. It is represented as 1D
array o[] where we store indexes
of all matching words as a bitmap for
current state.
- 匹配: 在构建的自动机上遍历给定的文本以找到所有匹配的单词。
预处理:
- 我们首先建立一个 崔 (或关键字树)的所有单词。
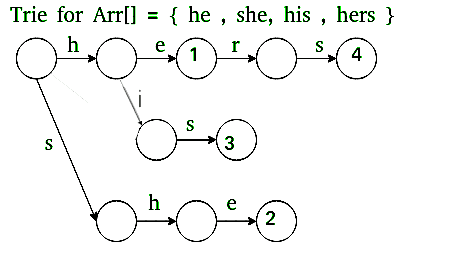
崔
- 这部分填写goto g[]和output o[]中的条目。
- 接下来,我们将Trie扩展为一个自动机,以支持线性时间匹配。

- 该部分填写故障f[]中的条目,并输出o[]。
去: 我们建造 崔 .对于所有根上没有边的字符,我们将边添加回根。 失败: 对于状态s,我们找到最长的适当后缀,它是某种模式的适当前缀。这是使用Trie的宽度优先遍历来完成的。 输出: 对于状态s,存储以s结尾的所有单词的索引。这些索引存储为按位映射(通过按位或按值)。这也是使用带故障的广度优先遍历进行计算。
下面是Aho Corasick算法的实现
C++
// C++ program for implementation of Aho Corasick algorithm // for string matching using namespace std; #include <bits/stdc++.h> // Max number of states in the matching machine. // Should be equal to the sum of the length of all keywords. const int MAXS = 500; // Maximum number of characters in input alphabet const int MAXC = 26; // OUTPUT FUNCTION IS IMPLEMENTED USING out[] // Bit i in this mask is one if the word with index i // appears when the machine enters this state. int out[MAXS]; // FAILURE FUNCTION IS IMPLEMENTED USING f[] int f[MAXS]; // GOTO FUNCTION (OR TRIE) IS IMPLEMENTED USING g[][] int g[MAXS][MAXC]; // Builds the string matching machine. // arr - array of words. The index of each keyword is important: // "out[state] & (1 << i)" is > 0 if we just found word[i] // in the text. // Returns the number of states that the built machine has. // States are numbered 0 up to the return value - 1, inclusive. int buildMatchingMachine(string arr[], int k) { // Initialize all values in output function as 0. memset (out, 0, sizeof out); // Initialize all values in goto function as -1. memset (g, -1, sizeof g); // Initially, we just have the 0 state int states = 1; // Construct values for goto function, i.e., fill g[][] // This is same as building a Trie for arr[] for ( int i = 0; i < k; ++i) { const string &word = arr[i]; int currentState = 0; // Insert all characters of current word in arr[] for ( int j = 0; j < word.size(); ++j) { int ch = word[j] - 'a' ; // Allocate a new node (create a new state) if a // node for ch doesn't exist. if (g[currentState][ch] == -1) g[currentState][ch] = states++; currentState = g[currentState][ch]; } // Add current word in output function out[currentState] |= (1 << i); } // For all characters which don't have an edge from // root (or state 0) in Trie, add a goto edge to state // 0 itself for ( int ch = 0; ch < MAXC; ++ch) if (g[0][ch] == -1) g[0][ch] = 0; // Now, let's build the failure function // Initialize values in fail function memset (f, -1, sizeof f); // Failure function is computed in breadth first order // using a queue queue< int > q; // Iterate over every possible input for ( int ch = 0; ch < MAXC; ++ch) { // All nodes of depth 1 have failure function value // as 0. For example, in above diagram we move to 0 // from states 1 and 3. if (g[0][ch] != 0) { f[g[0][ch]] = 0; q.push(g[0][ch]); } } // Now queue has states 1 and 3 while (q.size()) { // Remove the front state from queue int state = q.front(); q.pop(); // For the removed state, find failure function for // all those characters for which goto function is // not defined. for ( int ch = 0; ch <= MAXC; ++ch) { // If goto function is defined for character 'ch' // and 'state' if (g[state][ch] != -1) { // Find failure state of removed state int failure = f[state]; // Find the deepest node labeled by proper // suffix of string from root to current // state. while (g[failure][ch] == -1) failure = f[failure]; failure = g[failure][ch]; f[g[state][ch]] = failure; // Merge output values out[g[state][ch]] |= out[failure]; // Insert the next level node (of Trie) in Queue q.push(g[state][ch]); } } } return states; } // Returns the next state the machine will transition to using goto // and failure functions. // currentState - The current state of the machine. Must be between // 0 and the number of states - 1, inclusive. // nextInput - The next character that enters into the machine. int findNextState( int currentState, char nextInput) { int answer = currentState; int ch = nextInput - 'a' ; // If goto is not defined, use failure function while (g[answer][ch] == -1) answer = f[answer]; return g[answer][ch]; } // This function finds all occurrences of all array words // in text. void searchWords(string arr[], int k, string text) { // Preprocess patterns. // Build machine with goto, failure and output functions buildMatchingMachine(arr, k); // Initialize current state int currentState = 0; // Traverse the text through the built machine to find // all occurrences of words in arr[] for ( int i = 0; i < text.size(); ++i) { currentState = findNextState(currentState, text[i]); // If match not found, move to next state if (out[currentState] == 0) continue ; // Match found, print all matching words of arr[] // using output function. for ( int j = 0; j < k; ++j) { if (out[currentState] & (1 << j)) { cout << "Word " << arr[j] << " appears from " << i - arr[j].size() + 1 << " to " << i << endl; } } } } // Driver program to test above int main() { string arr[] = { "he" , "she" , "hers" , "his" }; string text = "ahishers" ; int k = sizeof (arr)/ sizeof (arr[0]); searchWords(arr, k, text); return 0; } |
JAVA
// Java program for implementation of // Aho Corasick algorithm for String // matching import java.util.*; class GFG{ // Max number of states in the matching // machine. Should be equal to the sum // of the length of all keywords. static int MAXS = 500 ; // Maximum number of characters // in input alphabet static int MAXC = 26 ; // OUTPUT FUNCTION IS IMPLEMENTED USING out[] // Bit i in this mask is one if the word with // index i appears when the machine enters // this state. static int []out = new int [MAXS]; // FAILURE FUNCTION IS IMPLEMENTED USING f[] static int []f = new int [MAXS]; // GOTO FUNCTION (OR TRIE) IS // IMPLEMENTED USING g[][] static int [][]g = new int [MAXS][MAXC]; // Builds the String matching machine. // arr - array of words. The index of each keyword is important: // "out[state] & (1 << i)" is > 0 if we just found word[i] // in the text. // Returns the number of states that the built machine has. // States are numbered 0 up to the return value - 1, inclusive. static int buildMatchingMachine(String arr[], int k) { // Initialize all values in output function as 0. Arrays.fill(out, 0 ); // Initialize all values in goto function as -1. for ( int i = 0 ; i < MAXS; i++) Arrays.fill(g[i], - 1 ); // Initially, we just have the 0 state int states = 1 ; // Convalues for goto function, i.e., fill g[][] // This is same as building a Trie for arr[] for ( int i = 0 ; i < k; ++i) { String word = arr[i]; int currentState = 0 ; // Insert all characters of current // word in arr[] for ( int j = 0 ; j < word.length(); ++j) { int ch = word.charAt(j) - 'a' ; // Allocate a new node (create a new state) // if a node for ch doesn't exist. if (g[currentState][ch] == - 1 ) g[currentState][ch] = states++; currentState = g[currentState][ch]; } // Add current word in output function out[currentState] |= ( 1 << i); } // For all characters which don't have // an edge from root (or state 0) in Trie, // add a goto edge to state 0 itself for ( int ch = 0 ; ch < MAXC; ++ch) if (g[ 0 ][ch] == - 1 ) g[ 0 ][ch] = 0 ; // Now, let's build the failure function // Initialize values in fail function Arrays.fill(f, - 1 ); // Failure function is computed in // breadth first order // using a queue Queue<Integer> q = new LinkedList<>(); // Iterate over every possible input for ( int ch = 0 ; ch < MAXC; ++ch) { // All nodes of depth 1 have failure // function value as 0. For example, // in above diagram we move to 0 // from states 1 and 3. if (g[ 0 ][ch] != 0 ) { f[g[ 0 ][ch]] = 0 ; q.add(g[ 0 ][ch]); } } // Now queue has states 1 and 3 while (!q.isEmpty()) { // Remove the front state from queue int state = q.peek(); q.remove(); // For the removed state, find failure // function for all those characters // for which goto function is // not defined. for ( int ch = 0 ; ch < MAXC; ++ch) { // If goto function is defined for // character 'ch' and 'state' if (g[state][ch] != - 1 ) { // Find failure state of removed state int failure = f[state]; // Find the deepest node labeled by proper // suffix of String from root to current // state. while (g[failure][ch] == - 1 ) failure = f[failure]; failure = g[failure][ch]; f[g[state][ch]] = failure; // Merge output values out[g[state][ch]] |= out[failure]; // Insert the next level node // (of Trie) in Queue q.add(g[state][ch]); } } } return states; } // Returns the next state the machine will transition to using goto // and failure functions. // currentState - The current state of the machine. Must be between // 0 and the number of states - 1, inclusive. // nextInput - The next character that enters into the machine. static int findNextState( int currentState, char nextInput) { int answer = currentState; int ch = nextInput - 'a' ; // If goto is not defined, use // failure function while (g[answer][ch] == - 1 ) answer = f[answer]; return g[answer][ch]; } // This function finds all occurrences of // all array words in text. static void searchWords(String arr[], int k, String text) { // Preprocess patterns. // Build machine with goto, failure // and output functions buildMatchingMachine(arr, k); // Initialize current state int currentState = 0 ; // Traverse the text through the // built machine to find all // occurrences of words in arr[] for ( int i = 0 ; i < text.length(); ++i) { currentState = findNextState(currentState, text.charAt(i)); // If match not found, move to next state if (out[currentState] == 0 ) continue ; // Match found, print all matching // words of arr[] // using output function. for ( int j = 0 ; j < k; ++j) { if ((out[currentState] & ( 1 << j)) > 0 ) { System.out.print( "Word " + arr[j] + " appears from " + (i - arr[j].length() + 1 ) + " to " + i + "" ); } } } } // Driver code public static void main(String[] args) { String arr[] = { "he" , "she" , "hers" , "his" }; String text = "ahishers" ; int k = arr.length; searchWords(arr, k, text); } } // This code is contributed by Princi Singh |
Python3
# Python program for implementation of # Aho-Corasick algorithm for string matching # defaultdict is used only for storing the final output # We will return a dictionary where key is the matched word # and value is the list of indexes of matched word from collections import defaultdict # For simplicity, Arrays and Queues have been implemented using lists. # If you want to improve performance try using them instead class AhoCorasick: def __init__( self , words): # Max number of states in the matching machine. # Should be equal to the sum of the length of all keywords. self .max_states = sum ([ len (word) for word in words]) # Maximum number of characters. # Currently supports only alphabets [a,z] self .max_characters = 26 # OUTPUT FUNCTION IS IMPLEMENTED USING out [] # Bit i in this mask is 1 if the word with # index i appears when the machine enters this state. # Lets say, a state outputs two words "he" and "she" and # in our provided words list, he has index 0 and she has index 3 # so value of out[state] for this state will be 1001 # It has been initialized to all 0. # We have taken one extra state for the root. self .out = [ 0 ] * ( self .max_states + 1 ) # FAILURE FUNCTION IS IMPLEMENTED USING fail [] # There is one value for each state + 1 for the root # It has been initialized to all -1 # This will contain the fail state value for each state self .fail = [ - 1 ] * ( self .max_states + 1 ) # GOTO FUNCTION (OR TRIE) IS IMPLEMENTED USING goto [[]] # Number of rows = max_states + 1 # Number of columns = max_characters i.e 26 in our case # It has been initialized to all -1. self .goto = [[ - 1 ] * self .max_characters for _ in range ( self .max_states + 1 )] # Convert all words to lowercase # so that our search is case insensitive for i in range ( len (words)): words[i] = words[i].lower() # All the words in dictionary which will be used to create Trie # The index of each keyword is important: # "out[state] & (1 << i)" is > 0 if we just found word[i] # in the text. self .words = words # Once the Trie has been built, it will contain the number # of nodes in Trie which is total number of states required <= max_states self .states_count = self .__build_matching_machine() # Builds the String matching machine. # Returns the number of states that the built machine has. # States are numbered 0 up to the return value - 1, inclusive. def __build_matching_machine( self ): k = len ( self .words) # Initially, we just have the 0 state states = 1 # Convalues for goto function, i.e., fill goto # This is same as building a Trie for words[] for i in range (k): word = self .words[i] current_state = 0 # Process all the characters of the current word for character in word: ch = ord (character) - 97 # Ascii value of 'a' = 97 # Allocate a new node (create a new state) # if a node for ch doesn't exist. if self .goto[current_state][ch] = = - 1 : self .goto[current_state][ch] = states states + = 1 current_state = self .goto[current_state][ch] # Add current word in output function self .out[current_state] | = ( 1 <<i) # For all characters which don't have # an edge from root (or state 0) in Trie, # add a goto edge to state 0 itself for ch in range ( self .max_characters): if self .goto[ 0 ][ch] = = - 1 : self .goto[ 0 ][ch] = 0 # Failure function is computed in # breadth first order using a queue queue = [] # Iterate over every possible input for ch in range ( self .max_characters): # All nodes of depth 1 have failure # function value as 0. For example, # in above diagram we move to 0 # from states 1 and 3. if self .goto[ 0 ][ch] ! = 0 : self .fail[ self .goto[ 0 ][ch]] = 0 queue.append( self .goto[ 0 ][ch]) # Now queue has states 1 and 3 while queue: # Remove the front state from queue state = queue.pop( 0 ) # For the removed state, find failure # function for all those characters # for which goto function is not defined. for ch in range ( self .max_characters): # If goto function is defined for # character 'ch' and 'state' if self .goto[state][ch] ! = - 1 : # Find failure state of removed state failure = self .fail[state] # Find the deepest node labeled by proper # suffix of String from root to current state. while self .goto[failure][ch] = = - 1 : failure = self .fail[failure] failure = self .goto[failure][ch] self .fail[ self .goto[state][ch]] = failure # Merge output values self .out[ self .goto[state][ch]] | = self .out[failure] # Insert the next level node (of Trie) in Queue queue.append( self .goto[state][ch]) return states # Returns the next state the machine will transition to using goto # and failure functions. # current_state - The current state of the machine. Must be between # 0 and the number of states - 1, inclusive. # next_input - The next character that enters into the machine. def __find_next_state( self , current_state, next_input): answer = current_state ch = ord (next_input) - 97 # Ascii value of 'a' is 97 # If goto is not defined, use # failure function while self .goto[answer][ch] = = - 1 : answer = self .fail[answer] return self .goto[answer][ch] # This function finds all occurrences of all words in text. def search_words( self , text): # Convert the text to lowercase to make search case insensitive text = text.lower() # Initialize current_state to 0 current_state = 0 # A dictionary to store the result. # Key here is the found word # Value is a list of all occurrences start index result = defaultdict( list ) # Traverse the text through the built machine # to find all occurrences of words for i in range ( len (text)): current_state = self .__find_next_state(current_state, text[i]) # If match not found, move to next state if self .out[current_state] = = 0 : continue # Match found, store the word in result dictionary for j in range ( len ( self .words)): if ( self .out[current_state] & ( 1 <<j)) > 0 : word = self .words[j] # Start index of word is (i-len(word)+1) result[word].append(i - len (word) + 1 ) # Return the final result dictionary return result # Driver code if __name__ = = "__main__" : words = [ "he" , "she" , "hers" , "his" ] text = "ahishers" # Create an Object to initialize the Trie aho_chorasick = AhoCorasick(words) # Get the result result = aho_chorasick.search_words(text) # Print the result for word in result: for i in result[word]: print ( "Word" , word, "appears from" , i, "to" , i + len (word) - 1 ) # This code is contributed by Md Azharuddin |
C#
// C# program for implementation of // Aho Corasick algorithm for String // matching using System; using System.Collections.Generic; class GFG{ // Max number of states in the matching // machine. Should be equal to the sum // of the length of all keywords. static int MAXS = 500; // Maximum number of characters // in input alphabet static int MAXC = 26; // OUTPUT FUNCTION IS IMPLEMENTED USING out[] // Bit i in this mask is one if the word with // index i appears when the machine enters // this state. static int [] out = new int [MAXS]; // FAILURE FUNCTION IS IMPLEMENTED USING f[] static int [] f = new int [MAXS]; // GOTO FUNCTION (OR TRIE) IS // IMPLEMENTED USING g[,] static int [,] g = new int [MAXS, MAXC]; // Builds the String matching machine. // arr - array of words. The index of each keyword is // important: // "out[state] & (1 << i)" is > 0 if we just // found word[i] in the text. // Returns the number of states that the built machine // has. States are numbered 0 up to the return value - // 1, inclusive. static int buildMatchingMachine(String[] arr, int k) { // Initialize all values in output function as 0. for ( int i = 0; i < outt.Length; i++) outt[i] = 0; // Initialize all values in goto function as -1. for ( int i = 0; i < MAXS; i++) for ( int j = 0; j < MAXC; j++) g[i, j] = -1; // Initially, we just have the 0 state int states = 1; // Convalues for goto function, i.e., fill g[,] // This is same as building a Trie for []arr for ( int i = 0; i < k; ++i) { String word = arr[i]; int currentState = 0; // Insert all characters of current // word in []arr for ( int j = 0; j < word.Length; ++j) { int ch = word[j] - 'a' ; // Allocate a new node (create a new state) // if a node for ch doesn't exist. if (g[currentState, ch] == -1) g[currentState, ch] = states++; currentState = g[currentState, ch]; } // Add current word in output function outt[currentState] |= (1 << i); } // For all characters which don't have // an edge from root (or state 0) in Trie, // add a goto edge to state 0 itself for ( int ch = 0; ch < MAXC; ++ch) if (g[0, ch] == -1) g[0, ch] = 0; // Now, let's build the failure function // Initialize values in fail function for ( int i = 0; i < MAXC; i++) f[i] = 0; // Failure function is computed in // breadth first order // using a queue Queue< int > q = new Queue< int >(); // Iterate over every possible input for ( int ch = 0; ch < MAXC; ++ch) { // All nodes of depth 1 have failure // function value as 0. For example, // in above diagram we move to 0 // from states 1 and 3. if (g[0, ch] != 0) { f[g[0, ch]] = 0; q.Enqueue(g[0, ch]); } } // Now queue has states 1 and 3 while (q.Count != 0) { // Remove the front state from queue int state = q.Peek(); q.Dequeue(); // For the removed state, find failure // function for all those characters // for which goto function is // not defined. for ( int ch = 0; ch < MAXC; ++ch) { // If goto function is defined for // character 'ch' and 'state' if (g[state, ch] != -1) { // Find failure state of removed state int failure = f[state]; // Find the deepest node labeled by // proper suffix of String from root to // current state. while (g[failure, ch] == -1) failure = f[failure]; failure = g[failure, ch]; f[g[state, ch]] = failure; // Merge output values outt[g[state, ch]] |= outt[failure]; // Insert the next level node // (of Trie) in Queue q.Enqueue(g[state, ch]); } } } return states; } // Returns the next state the machine will transition to // using goto and failure functions. currentState - The // current state of the machine. Must be between // 0 and the number of states - 1, // inclusive. // nextInput - The next character that enters into the // machine. static int findNextState( int currentState, char nextInput) { int answer = currentState; int ch = nextInput - 'a' ; // If goto is not defined, use // failure function while (g[answer, ch] == -1) answer = f[answer]; return g[answer, ch]; } // This function finds all occurrences of // all array words in text. static void searchWords(String[] arr, int k, String text) { // Preprocess patterns. // Build machine with goto, failure // and output functions buildMatchingMachine(arr, k); // Initialize current state int currentState = 0; // Traverse the text through the // built machine to find all // occurrences of words in []arr for ( int i = 0; i < text.Length; ++i) { currentState = findNextState(currentState, text[i]); // If match not found, move to next state if (outt[currentState] == 0) continue ; // Match found, print all matching // words of []arr // using output function. for ( int j = 0; j < k; ++j) { if ((outt[currentState] & (1 << j)) > 0) { Console.Write( "Word " + arr[j] + " appears from " + (i - arr[j].Length + 1) + " to " + i + "" ); } } } } // Driver code public static void Main(String[] args) { String[] arr = { "he" , "she" , "hers" , "his" }; String text = "ahishers" ; int k = arr.Length; searchWords(arr, k, text); } } // This code is contributed by Amit Katiyar |
Word his appears from 1 to 3 Word he appears from 4 to 5 Word she appears from 3 to 5 Word hers appears from 4 to 7
资料来源: http://www.cs.uku.fi/~kilpelai/BSA05/讲座/幻灯片04。pdf 本文由 阿尤什·戈维尔 。如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请发表评论


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



