给定一个数字n,打印所有小于或等于n的素数。 例如:
null
Input: n = 10Output: 2, 3, 5, 7Input: n = 20Output: 2, 3, 5, 7, 11, 13, 17, 19
我们讨论过 埃拉托斯坦筛 上述任务的算法。 下面是Sundaram算法的筛选。
printPrimes(n)[Prints all prime numbers smaller than n]1) In general Sieve of Sundaram, produces primes smaller than (2*x + 2) for a number given number x. Since we want primes smaller than n, we reduce n-1 to half. We call it nNew. nNew = (n-1)/2; For example, if n = 102, then nNew = 50. if n = 103, then nNew = 512) Create an array marked[n] that is going to be used to separate numbers of the form i+j+2ij from others where 1 <= i <= j3) Initialize all entries of marked[] as false.4) // Mark all numbers of the form i + j + 2ij as true // where 1 <= i <= j Loop for i=1 to nNew a) j = i; b) Loop While (i + j + 2*i*j) 2, then print 2 as first prime.6) Remaining primes are of the form 2i + 1 where i is index of NOT marked numbers. So print 2i + 1 for all i such that marked[i] is false.
下面是上述算法的实现:
C++
// C++ program to print primes smaller than n using // Sieve of Sundaram. #include <bits/stdc++.h> using namespace std; // Prints all prime numbers smaller int SieveOfSundaram( int n) { // In general Sieve of Sundaram, produces primes smaller // than (2*x + 2) for a number given number x. // Since we want primes smaller than n, we reduce n to half int nNew = (n-1)/2; // This array is used to separate numbers of the form i+j+2ij // from others where 1 <= i <= j bool marked[nNew + 1]; // Initialize all elements as not marked memset (marked, false , sizeof (marked)); // Main logic of Sundaram. Mark all numbers of the // form i + j + 2ij as true where 1 <= i <= j for ( int i=1; i<=nNew; i++) for ( int j=i; (i + j + 2*i*j) <= nNew; j++) marked[i + j + 2*i*j] = true ; // Since 2 is a prime number if (n > 2) cout << 2 << " " ; // Print other primes. Remaining primes are of the form // 2*i + 1 such that marked[i] is false. for ( int i=1; i<=nNew; i++) if (marked[i] == false ) cout << 2*i + 1 << " " ; } // Driver program to test above int main( void ) { int n = 20; SieveOfSundaram(n); return 0; } |
JAVA
// Java program to print primes smaller // than n using Sieve of Sundaram. import java.util.Arrays; class GFG { // Prints all prime numbers smaller static int SieveOfSundaram( int n) { // In general Sieve of Sundaram, produces // primes smaller than (2*x + 2) for a number // given number x. Since we want primes // smaller than n, we reduce n to half int nNew = (n - 1 ) / 2 ; // This array is used to separate numbers of the // form i+j+2ij from others where 1 <= i <= j boolean marked[] = new boolean [nNew + 1 ]; // Initialize all elements as not marked Arrays.fill(marked, false ); // Main logic of Sundaram. Mark all numbers of the // form i + j + 2ij as true where 1 <= i <= j for ( int i = 1 ; i <= nNew; i++) for ( int j = i; (i + j + 2 * i * j) <= nNew; j++) marked[i + j + 2 * i * j] = true ; // Since 2 is a prime number if (n > 2 ) System.out.print( 2 + " " ); // Print other primes. Remaining primes are of // the form 2*i + 1 such that marked[i] is false. for ( int i = 1 ; i <= nNew; i++) if (marked[i] == false ) System.out.print( 2 * i + 1 + " " ); return - 1 ; } // Driver code public static void main(String[] args) { int n = 20 ; SieveOfSundaram(n); } } // This code is contributed by Anant Agarwal. |
Python3
# Python3 program to print # primes smaller than n using # Sieve of Sundaram. # Prints all prime numbers smaller def SieveOfSundaram(n): # In general Sieve of Sundaram, # produces primes smaller # than (2*x + 2) for a number # given number x. Since we want # primes smaller than n, we # reduce n to half nNew = int ((n - 1 ) / 2 ); # This array is used to separate # numbers of the form i+j+2ij # from others where 1 <= i <= j # Initialize all elements as not marked marked = [ 0 ] * (nNew + 1 ); # Main logic of Sundaram. Mark all # numbers of the form i + j + 2ij # as true where 1 <= i <= j for i in range ( 1 , nNew + 1 ): j = i; while ((i + j + 2 * i * j) < = nNew): marked[i + j + 2 * i * j] = 1 ; j + = 1 ; # Since 2 is a prime number if (n > 2 ): print ( 2 , end = " " ); # Print other primes. Remaining # primes are of the form 2*i + 1 # such that marked[i] is false. for i in range ( 1 , nNew + 1 ): if (marked[i] = = 0 ): print (( 2 * i + 1 ), end = " " ); # Driver Code n = 20 ; SieveOfSundaram(n); # This code is contributed by mits |
C#
// C# program to print primes smaller // than n using Sieve of Sundaram. using System; class GFG { // Prints all prime numbers smaller static int SieveOfSundaram( int n) { // In general Sieve of Sundaram, produces // primes smaller than (2*x + 2) for a number // given number x. Since we want primes // smaller than n, we reduce n to half int nNew = (n - 1) / 2; // This array is used to separate // numbers of the form i+j+2ij from // others where 1 <= i <= j bool []marked = new bool [nNew + 1]; // Initialize all elements as not marked for ( int i=0;i<nNew+1;i++) marked[i]= false ; // Main logic of Sundaram. // Mark all numbers of the // form i + j + 2ij as true // where 1 <= i <= j for ( int i = 1; i <= nNew; i++) for ( int j = i; (i + j + 2 * i * j) <= nNew; j++) marked[i + j + 2 * i * j] = true ; // Since 2 is a prime number if (n > 2) Console.Write(2 + " " ); // Print other primes. // Remaining primes are of // the form 2*i + 1 such // that marked[i] is false. for ( int i = 1; i <= nNew; i++) if (marked[i] == false ) Console.Write(2 * i + 1 + " " ); return -1; } // Driver code public static void Main() { int n = 20; SieveOfSundaram(n); } } // This code is contributed by nitin mittal |
PHP
<?php // PHP program to print primes smaller // than n using Sieve of Sundaram. // Prints all prime numbers smaller function SieveOfSundaram( $n ) { // In general Sieve of Sundaram, // produces primes smaller than // (2*x + 2) for a number given // number x. Since we want primes // smaller than n, we reduce n to half $nNew = ( $n - 1) / 2; // This array is used to separate // numbers of the form i+j+2ij // from others where 1 <= i <= j // Initialize all elements as not marked $marked = array_fill (0, ( $nNew + 1), false); // Main logic of Sundaram. Mark all // numbers of the form i + j + 2ij // as true where 1 <= i <= j for ( $i = 1; $i <= $nNew ; $i ++) for ( $j = $i ; ( $i + $j + 2 * $i * $j ) <= $nNew ; $j ++) $marked [ $i + $j + 2 * $i * $j ] = true; // Since 2 is a prime number if ( $n > 2) echo "2 " ; // Print other primes. Remaining // primes are of the form 2*i + 1 // such that marked[i] is false. for ( $i = 1; $i <= $nNew ; $i ++) if ( $marked [ $i ] == false) echo (2 * $i + 1) . " " ; } // Driver Code $n = 20; SieveOfSundaram( $n ); // This code is contributed by mits ?> |
Javascript
<script> // JavaScript program to print primes smaller // than n using Sieve of Sundaram. // Prints all prime numbers smaller function SieveOfSundaram(n) { // In general Sieve of Sundaram, produces // primes smaller than (2*x + 2) for a number // given number x. Since we want primes // smaller than n, we reduce n to half let nNew = (n - 1) / 2; // This array is used to separate // numbers of the form i+j+2ij from // others where 1 <= i <= j let marked = []; // Initialize all elements as not marked for (let i = 0; i < nNew + 1; i++) marked[i] = false ; // Main logic of Sundaram. // Mark all numbers of the // form i + j + 2ij as true // where 1 <= i <= j for (let i = 1; i <= nNew; i++) for (let j = i; (i + j + 2 * i * j) <= nNew; j++) marked[i + j + 2 * i * j] = true ; // Since 2 is a prime number if (n > 2) document.write(2 + " " ); // Print other primes. // Remaining primes are of // the form 2*i + 1 such // that marked[i] is false. for (let i = 1; i <= nNew; i++) if (marked[i] == false ) document.write(2 * i + 1 + " " ); return -1; } // Driver program let n = 20; SieveOfSundaram(n); // This code is contributed by susmitakundugoaldanga. </script> |
2 3 5 7 11 13 17 19
插图: 下图中的所有红色条目均为标记条目。对于每个剩余的(或黑色)条目x,数字2x+1是素数。 让我们看看它在n=102时是如何工作的,我们将有(n-1)/2的筛子,如下所示:
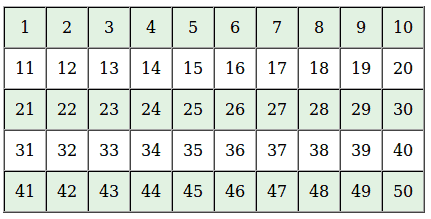
标记所有可以表示为i+j+2ij的数字
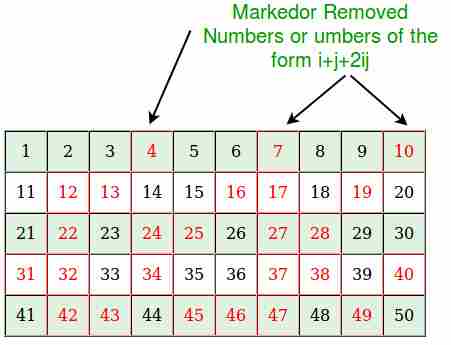
现在,对于列表中所有未标记的数字,找到2x+1,这将是素数: 比如2*1+1=3 2*3+1=7 2*5+1=11 2*6+1=13 2*8+1=17,依此类推。。 这是怎么回事? 当我们生成最终输出时,我们生成所有形式为2x+1的整数(也就是说,它们是奇数),除了单独处理的2。
Let q be an integer of the form 2x + 1.q is excluded if and only if x is of the form i + j + 2ij. That means, q = 2(i + j + 2ij) + 1 = (2i + 1)(2j + 1)So, an odd integer is excluded from the final list if and only if it has a factorization of the form (2i + 1)(2j + 1)which is to say, if it has a non-trivial odd factor. Source: Wiki
参考: https://en.wikipedia.org/wiki/Sieve_of_Sundaram 本文由 Anuj Rathore 。如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请发表评论
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



