重光分解|集1（简介）

重光分解（HLD）是其中一种 竞争性编程中最常用的技术 .

示例问题： 让我们通过下面的例子来了解重-轻分解（HLD）。

假设我们有 n个节点的不平衡树（不一定是二叉树） ，我们必须在树上执行操作以回答大量查询，每个查询可以是以下两种类型之一：

1. 改变（a，b） ：更新a的重量 ^th 边缘到b。
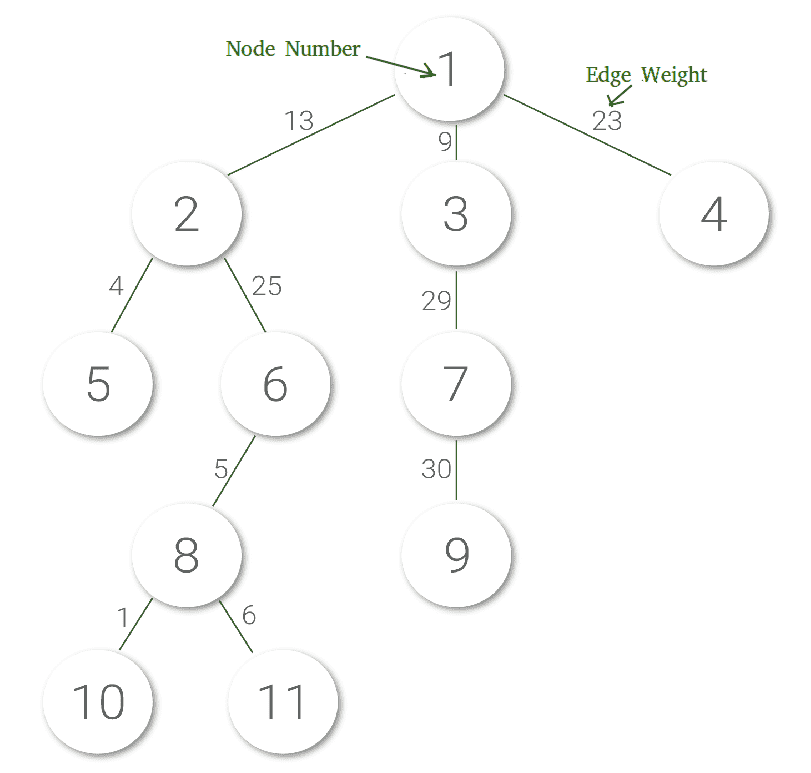
2. maxEdge（a，b） ：打印从节点a到节点b的路径上的最大边权重。例如，maxEdge（5，10）应打印25。

假设节点编号从1到n。必须有 n-1边 .边权重是自然数。还假设这两种类型的查询都是分散的（数量大致相等），因此没有哪种类型可以被边缘化以降低复杂性。

简单的解决方案： 一个简单的解决方案是遍历任何查询的完整树。该解决方案中每个查询的时间复杂度为O（n）。

本文中讨论的基于HLD的解决方案需要O（log ^2. （n） ）表示maxEdge（），O（logn）表示change（）。

大小 一个节点x的根数是以节点x为根的子树中的节点数。下面的图像显示了每个节点的子树大小，这些子树大小写在它们上面：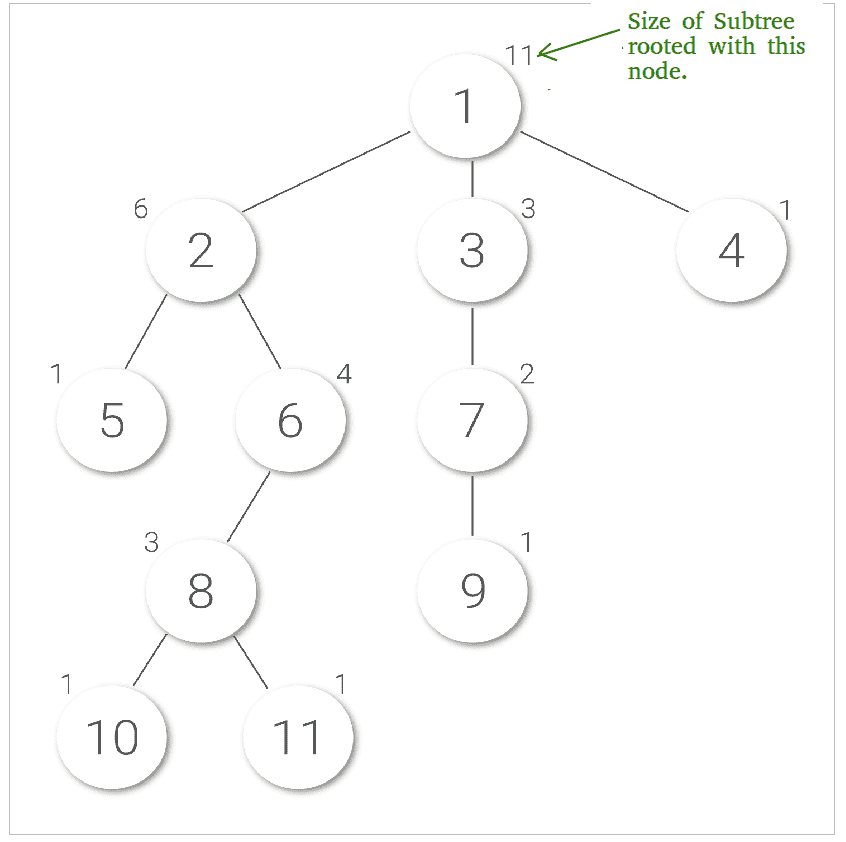

有根树的HLD是一种将树的顶点分解为不相交链（没有两条链共享一个节点）的方法，以实现涉及树的某些问题的重要渐近时间界。

HLD也可以被视为 “着色 “树的边缘。“重光”来自我们的生活方式 隔离并区别对待 边缘。我们使用 子树的大小 以节点为标准。

优势是 重的 如果大小（v）>大小（u），其中u是v的任何兄弟。如果它们相等，我们选择任何一个，比如v作为特殊。

改变（u，v）操作： 自从 分段树 作为表示单个链的底层数据结构，使用的更新完成更改 分段树 .所以 变化的时间复杂性 操作为O（日志n）。

maxEdge（u，v）操作：

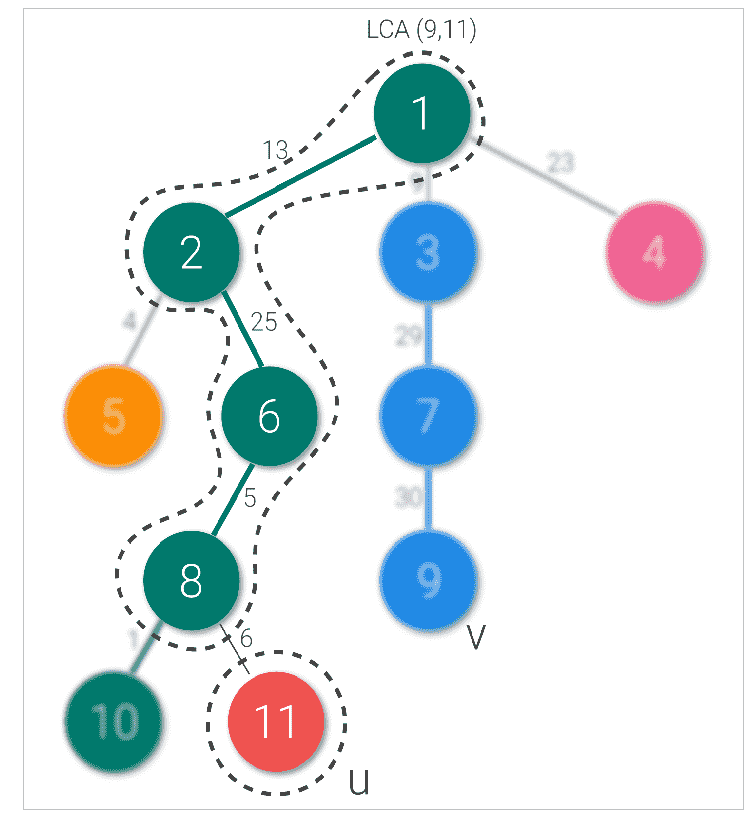
1. 我们首先找到两个节点的LCA。假设节点u是11，节点v是9。他们的生命周期评价是节点1。
2. 然后我们爬上树从节点u到lca。如果节点u和lca属于同一条链，我们使用分段树从表示它们之间边的范围中找到最大值。否则，我们从u所属的链中找到最大值，然后改变链，在我们不在同一个链中时重复。
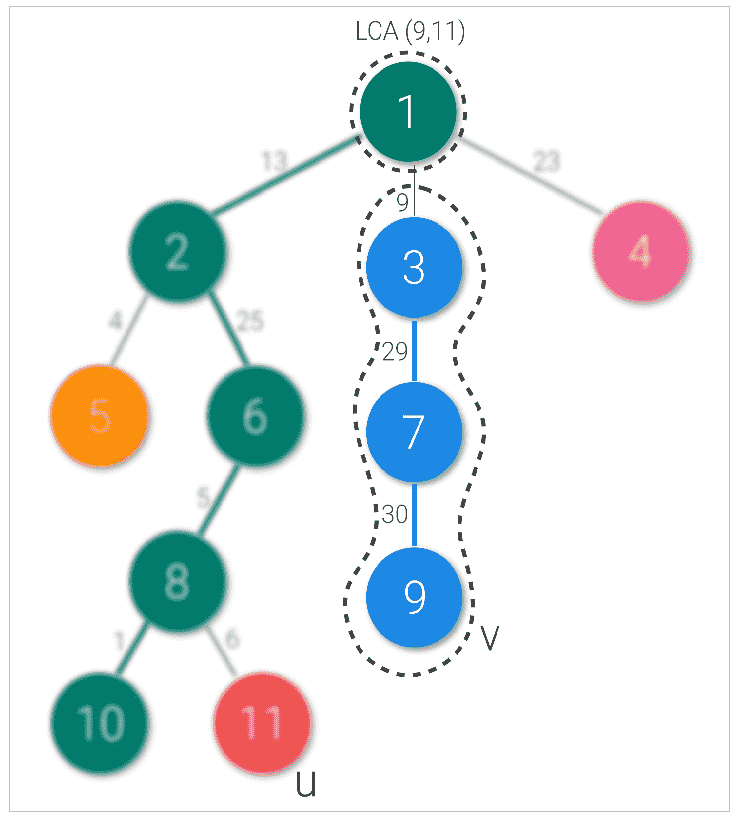
3. 我们从v到lca重复相同的步骤（如步骤2），并返回最大两个权重。

根据我们上面的例子，让我们把u作为节点11，v作为节点9。生命周期评价是节点1。我们从节点11移动到节点1，然后改变一次链。当我们更改链时，我们会从查询的节点转移到它所属链头的父节点（这里11个更改为8个）。类似地，查询节点9到节点3（包括灯光边缘），并更改链（节点更改为1）。

maxEdge的时间复杂度 是O（原木） ^2. （n） ）。查询链的最大值需要O（log（n））时间，因为链是用 分段树 最多有O（log（n））链。

链的数量是多少O（log（n））？ 所有链条都由一条光边连接（参见上面的示例）。所以链的数量是以任何路径上的光边的数量为界的。如果我们从根开始沿着一条光边，则在结果顶点处根的子树的大小最多为n/2。如果我们重复，我们降落在子树大小最多为n/4的顶点，以此类推。我们的结论是 从根到叶的任何路径上的光边数最多为对数（n） （来源： wcipeg )

非平衡树的重-轻分解的主要思想是将长（或重）路径的顶点以链的形式聚集在一起，这样就可以使用类似于段树的数据结构在O（logn）时间内查询这些线性链。

在 下一篇文章 作为例子，讨论了链的分段树表示以及HLD解决方案的实现。

重光分解|集2（实施）

本文由 亚什·瓦里亚尼 。如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请发表评论