给定一个有向图,找出该图是否强连通。如果任意两对顶点之间存在路径,则有向图是强连通的。例如,下面是一个强连通图。
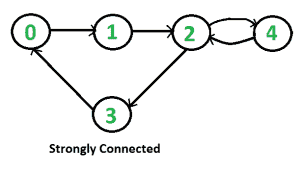
这对于无向图来说很容易 ,我们可以从任何顶点开始做BFS和DFS。如果BFS或DFS访问所有顶点,则给定的无向图是连通的。这种方法不适用于有向图。例如,考虑下面的图,它不是强连通的。如果我们从顶点0开始DFS(或BFS),我们可以到达所有顶点,但如果我们从任何其他顶点开始,我们无法到达所有顶点。

如何处理有向图?
一个简单的想法是使用全对最短路径算法,如 弗洛伊德·沃沙尔 或者找到 传递闭包 图的形式。该方法的时间复杂度为O(v) 3. ). 我们也可以 做 DFS V倍 从每个顶点开始。如果任何DFS未访问所有顶点,则图形不是强连通的。该算法需要O(V*(V+E))时间,这与稠密图的传递闭包相同。 更好的主意可能是 强连接组件(SCC) 算法 .我们可以在O(V+E)时间内找到所有SCC。若SCC数为1,则图是强连通的。SCC算法在查找所有SCC时会做额外的工作。 以下是 Kosaraju的基于DFS的简单算法,可以进行两次DFS遍历 图表的格式: 1) 将所有顶点初始化为未访问。 2) 从任意顶点v开始对图进行DFS遍历。如果DFS遍历没有访问所有顶点,则返回false。 3) 反转所有弧(或找到图形的转置或反转) 4) 在反向图中将所有顶点标记为未访问。 5) 从同一个顶点v开始进行反向图的DFS遍历(与步骤2相同)。如果DFS遍历没有访问所有顶点,则返回false。否则返回true。 其思想是,如果每个节点都可以从顶点v到达,并且每个节点都可以到达v,那么图是强连通的。在第2步中,我们检查所有顶点是否可以从v到达。在第4步中,我们检查所有顶点是否可以到达v(在反向图中,如果所有顶点都可以从v到达,那么所有顶点都可以到达原始图中的v)。 下面是上述算法的实现。
C++
// C++ program to check if a given directed graph is strongly // connected or not #include <iostream> #include <list> #include <stack> using namespace std; class Graph { int V; // No. of vertices list< int > *adj; // An array of adjacency lists // A recursive function to print DFS starting from v void DFSUtil( int v, bool visited[]); public : // Constructor and Destructor Graph( int V) { this ->V = V; adj = new list< int >[V];} ~Graph() { delete [] adj; } // Method to add an edge void addEdge( int v, int w); // The main function that returns true if the graph is strongly // connected, otherwise false bool isSC(); // Function that returns reverse (or transpose) of this graph Graph getTranspose(); }; // A recursive function to print DFS starting from v void Graph::DFSUtil( int v, bool visited[]) { // Mark the current node as visited and print it visited[v] = true ; // Recur for all the vertices adjacent to this vertex list< int >::iterator i; for (i = adj[v].begin(); i != adj[v].end(); ++i) if (!visited[*i]) DFSUtil(*i, visited); } // Function that returns reverse (or transpose) of this graph Graph Graph::getTranspose() { Graph g(V); for ( int v = 0; v < V; v++) { // Recur for all the vertices adjacent to this vertex list< int >::iterator i; for (i = adj[v].begin(); i != adj[v].end(); ++i) { g.adj[*i].push_back(v); } } return g; } void Graph::addEdge( int v, int w) { adj[v].push_back(w); // Add w to v’s list. } // The main function that returns true if graph is strongly connected bool Graph::isSC() { // St1p 1: Mark all the vertices as not visited (For first DFS) bool visited[V]; for ( int i = 0; i < V; i++) visited[i] = false ; // Step 2: Do DFS traversal starting from first vertex. DFSUtil(0, visited); // If DFS traversal doesn’t visit all vertices, then return false. for ( int i = 0; i < V; i++) if (visited[i] == false ) return false ; // Step 3: Create a reversed graph Graph gr = getTranspose(); // Step 4: Mark all the vertices as not visited (For second DFS) for ( int i = 0; i < V; i++) visited[i] = false ; // Step 5: Do DFS for reversed graph starting from first vertex. // Starting Vertex must be same starting point of first DFS gr.DFSUtil(0, visited); // If all vertices are not visited in second DFS, then // return false for ( int i = 0; i < V; i++) if (visited[i] == false ) return false ; return true ; } // Driver program to test above functions int main() { // Create graphs given in the above diagrams Graph g1(5); g1.addEdge(0, 1); g1.addEdge(1, 2); g1.addEdge(2, 3); g1.addEdge(3, 0); g1.addEdge(2, 4); g1.addEdge(4, 2); g1.isSC()? cout << "Yes" : cout << "No" ; Graph g2(4); g2.addEdge(0, 1); g2.addEdge(1, 2); g2.addEdge(2, 3); g2.isSC()? cout << "Yes" : cout << "No" ; return 0; } |
JAVA
// Java program to check if a given directed graph is strongly // connected or not import java.io.*; import java.util.*; import java.util.LinkedList; // This class represents a directed graph using adjacency // list representation class Graph { private int V; // No. of vertices private LinkedList<Integer> adj[]; //Adjacency List //Constructor Graph( int v) { V = v; adj = new LinkedList[v]; for ( int i= 0 ; i<v; ++i) adj[i] = new LinkedList(); } //Function to add an edge into the graph void addEdge( int v, int w) { adj[v].add(w); } // A recursive function to print DFS starting from v void DFSUtil( int v,Boolean visited[]) { // Mark the current node as visited and print it visited[v] = true ; int n; // Recur for all the vertices adjacent to this vertex Iterator<Integer> i = adj[v].iterator(); while (i.hasNext()) { n = i.next(); if (!visited[n]) DFSUtil(n,visited); } } // Function that returns transpose of this graph Graph getTranspose() { Graph g = new Graph(V); for ( int v = 0 ; v < V; v++) { // Recur for all the vertices adjacent to this vertex Iterator<Integer> i = adj[v].listIterator(); while (i.hasNext()) g.adj[i.next()].add(v); } return g; } // The main function that returns true if graph is strongly // connected Boolean isSC() { // Step 1: Mark all the vertices as not visited // (For first DFS) Boolean visited[] = new Boolean[V]; for ( int i = 0 ; i < V; i++) visited[i] = false ; // Step 2: Do DFS traversal starting from first vertex. DFSUtil( 0 , visited); // If DFS traversal doesn't visit all vertices, then // return false. for ( int i = 0 ; i < V; i++) if (visited[i] == false ) return false ; // Step 3: Create a reversed graph Graph gr = getTranspose(); // Step 4: Mark all the vertices as not visited (For // second DFS) for ( int i = 0 ; i < V; i++) visited[i] = false ; // Step 5: Do DFS for reversed graph starting from // first vertex. Starting Vertex must be same starting // point of first DFS gr.DFSUtil( 0 , visited); // If all vertices are not visited in second DFS, then // return false for ( int i = 0 ; i < V; i++) if (visited[i] == false ) return false ; return true ; } public static void main(String args[]) { // Create graphs given in the above diagrams Graph g1 = new Graph( 5 ); g1.addEdge( 0 , 1 ); g1.addEdge( 1 , 2 ); g1.addEdge( 2 , 3 ); g1.addEdge( 3 , 0 ); g1.addEdge( 2 , 4 ); g1.addEdge( 4 , 2 ); if (g1.isSC()) System.out.println( "Yes" ); else System.out.println( "No" ); Graph g2 = new Graph( 4 ); g2.addEdge( 0 , 1 ); g2.addEdge( 1 , 2 ); g2.addEdge( 2 , 3 ); if (g2.isSC()) System.out.println( "Yes" ); else System.out.println( "No" ); } } // This code is contributed by Aakash Hasija |
Python3
# Python program to check if a given directed graph is strongly # connected or not from collections import defaultdict # This class represents a directed graph using adjacency list representation class Graph: def __init__( self , vertices): self .V = vertices # No. of vertices self .graph = defaultdict( list ) # default dictionary to store graph # function to add an edge to graph def addEdge( self , u, v): self .graph[u].append(v) # A function used by isSC() to perform DFS def DFSUtil( self , v, visited): # Mark the current node as visited visited[v] = True # Recur for all the vertices adjacent to this vertex for i in self .graph[v]: if visited[i] = = False : self .DFSUtil(i, visited) # Function that returns reverse (or transpose) of this graph def getTranspose( self ): g = Graph( self .V) # Recur for all the vertices adjacent to this vertex for i in self .graph: for j in self .graph[i]: g.addEdge(j, i) return g # The main function that returns true if graph is strongly connected def isSC( self ): # Step 1: Mark all the vertices as not visited (For first DFS) visited = [ False ] * ( self .V) # Step 2: Do DFS traversal starting from first vertex. self .DFSUtil( 0 ,visited) # If DFS traversal doesnt visit all vertices, then return false if any (i = = False for i in visited): return False # Step 3: Create a reversed graph gr = self .getTranspose() # Step 4: Mark all the vertices as not visited (For second DFS) visited = [ False ] * ( self .V) # Step 5: Do DFS for reversed graph starting from first vertex. # Starting Vertex must be same starting point of first DFS gr.DFSUtil( 0 ,visited) # If all vertices are not visited in second DFS, then # return false if any (i = = False for i in visited): return False return True # Create a graph given in the above diagram g1 = Graph( 5 ) g1.addEdge( 0 , 1 ) g1.addEdge( 1 , 2 ) g1.addEdge( 2 , 3 ) g1.addEdge( 3 , 0 ) g1.addEdge( 2 , 4 ) g1.addEdge( 4 , 2 ) print ( "Yes" if g1.isSC() else "No" ) g2 = Graph( 4 ) g2.addEdge( 0 , 1 ) g2.addEdge( 1 , 2 ) g2.addEdge( 2 , 3 ) print ( "Yes" if g2.isSC() else "No" ) # This code is contributed by Neelam Yadav |
Javascript
<script> // Javascript program to check if a given directed graph is strongly // connected or not // This class represents a directed graph using adjacency // list representation class Graph { // Constructor constructor(v) { this .V = v; this .adj = new Array(v); for (let i = 0; i < v; ++i) this .adj[i] = []; } // Function to add an edge into the graph addEdge(v,w) { this .adj[v].push(w); } // A recursive function to print DFS starting from v DFSUtil(v,visited) { // Mark the current node as visited and print it visited[v] = true ; let n; // Recur for all the vertices adjacent to this vertex for (let i of this .adj[v].values()) { n = i; if (!visited[n]) this .DFSUtil(n,visited); } } // Function that returns transpose of this graph getTranspose() { let g = new Graph( this .V); for (let v = 0; v < this .V; v++) { // Recur for all the vertices adjacent to this vertex for (let i of this .adj[v].values()) g.adj[i].push(v); } return g; } // The main function that returns true if graph is strongly // connected isSC() { // Step 1: Mark all the vertices as not visited // (For first DFS) let visited = new Array( this .V); for (let i = 0; i < this .V; i++) visited[i] = false ; // Step 2: Do DFS traversal starting from first vertex. this .DFSUtil(0, visited); // If DFS traversal doesn't visit all vertices, then // return false. for (let i = 0; i < this .V; i++) if (visited[i] == false ) return false ; // Step 3: Create a reversed graph let gr = this .getTranspose(); // Step 4: Mark all the vertices as not visited (For // second DFS) for (let i = 0; i < this .V; i++) visited[i] = false ; // Step 5: Do DFS for reversed graph starting from // first vertex. Starting Vertex must be same starting // point of first DFS gr.DFSUtil(0, visited); // If all vertices are not visited in second DFS, then // return false for (let i = 0; i < this .V; i++) if (visited[i] == false ) return false ; return true ; } } // Create graphs given in the above diagrams let g1 = new Graph(5); g1.addEdge(0, 1); g1.addEdge(1, 2); g1.addEdge(2, 3); g1.addEdge(3, 0); g1.addEdge(2, 4); g1.addEdge(4, 2); if (g1.isSC()) document.write( "Yes<br>" ); else document.write( "No<br>" ); let g2 = new Graph(4); g2.addEdge(0, 1); g2.addEdge(1, 2); g2.addEdge(2, 3); if (g2.isSC()) document.write( "Yes" ); else document.write( "No" ); // This code is contributed by avanitrachhadiya2155 </script> |
输出:
YesNo
时间复杂性: 上述实现的时间复杂度与 深度优先搜索 如果图是用邻接列表表示的,那么它就是O(V+E)。 我们能进一步改进吗? 上述方法需要对图进行两次遍历。我们可以通过使用 Tarjan寻找强连通分量的算法 . 练习: 在上述算法中,我们能用BFS代替DFS吗?看见 这 . 参考资料: http://www.ieor.berkeley.edu/~hochbaum/files/ieor266-2012。pdf 如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写评论


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



