图的传递闭包-yiteyi-C++库

给定一个有向图，找出给定图中所有顶点对（i，j）的顶点j是否可以从另一个顶点i到达。这里的可达性意味着有一条从顶点i到j的路径。可达性矩阵被称为图的传递闭包。

null

For example, consider below graph

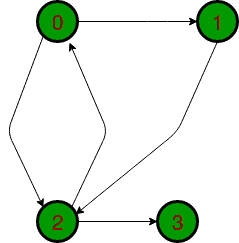
transitiveclosure

Transitive closure of above graphs is      1 1 1 1      1 1 1 1      1 1 1 1      0 0 0 1

建议：请在“上解决” 实践 “首先，在讨论解决方案之前。

图是以邻接矩阵的形式给出的，称为“图[V][V]”，其中图[i][j]是1，如果从顶点i到顶点j有一条边，或者i等于j，否则图[i][j]是0。弗洛伊德·沃沙尔算法可以使用，我们可以使用弗洛伊德·沃沙尔，如果dist[i][j]是无限的，那么j不能从i到达。否则，j是可到达的，dist[i][j]的值将小于V。对于这个特殊的问题，我们可以在空间和时间方面对其进行优化，而不是直接使用Floyd Warshall。以下是优化：

而不是整数合成矩阵( 弗洛伊德·沃沙尔区 )，我们可以创建一个布尔可达能力矩阵reach[V][V]（我们节省了空间）。如果从i可以到达j，则到达[i][j]的值为1，否则为0。
我们可以用逻辑运算代替算术运算。对于算术运算“+”，使用逻辑and“&&”，对于最小值，使用逻辑or“| |”。（我们通过一个恒定的因素节省时间。尽管时间复杂度是相同的）

以下是上述方法的实施情况：

C++

                         // Program for transitive closure                       
                         // using Floyd Warshall Algorithm                       
                         #include<stdio.h>                       
           
                         // Number of vertices in the graph                       
                         #define V 4                       
           
                         // A function to print the solution matrix                       
                         void                                     printSolution(                                     int                                     reach[][V]);                       
           
                         // Prints transitive closure of graph[][]                       
                         // using Floyd Warshall algorithm                       
                         void                                     transitiveClosure(                                     int                                     graph[][V])                       
                         {                       
                                                 /* reach[][] will be the output matrix                       
                                                 // that will finally have the                       
                                                 shortest distances between                       
                                                 every pair of vertices */                       
                                                 int                                     reach[V][V], i, j, k;                       
           
                                                 /* Initialize the solution matrix same                       
                                                 as input graph matrix. Or                       
                                                 we can say the initial values of                       
                                                 shortest distances are based                       
                                                 on shortest paths considering                       
                                                 no intermediate vertex. */                       
                                                 for                                     (i = 0; i < V; i++)                       
                                                 for                                     (j = 0; j < V; j++)                       
                                                 reach[i][j] = graph[i][j];                       
           
                                                 /* Add all vertices one by one to the                       
                                                 set of intermediate vertices.                       
                                                 ---> Before start of a iteration,                       
                                                 we have reachability values for                       
                                                 all pairs of vertices such that                       
                                                 the reachability values                       
                                                 consider only the vertices in                       
                                                 set {0, 1, 2, .. k-1} as                       
                                                 intermediate vertices.                       
                                                 ----> After the end of a iteration,                       
                                                 vertex no. k is added to the                       
                                                 set of intermediate vertices                       
                                                 and the set becomes {0, 1, .. k} */                       
                                                 for                                     (k = 0; k < V; k++)                       
                                                 {                       
                                                 // Pick all vertices as                       
                                                 // source one by one                       
                                                 for                                     (i = 0; i < V; i++)                       
                                                 {                       
                                                 // Pick all vertices as                       
                                                 // destination for the                       
                                                 // above picked source                       
                                                 for                                     (j = 0; j < V; j++)                       
                                                 {                       
                                                 // If vertex k is on a path                       
                                                 // from i to j,                       
                                                 // then make sure that the value                       
                                                 // of reach[i][j] is 1                       
                                                 reach[i][j] = reach[i][j] ||                       
                                                 (reach[i][k] && reach[k][j]);                       
                                                 }                       
                                                 }                       
                                                 }                       
           
                                                 // Print the shortest distance matrix                       
                                                 printSolution(reach);                       
                         }                       
           
                         /* A utility function to print solution */                       
                         void                                     printSolution(                                     int                                     reach[][V])                       
                         {                       
                                                 printf                                     (                                     "Following matrix is transitive"                                     );                       
                                                 printf                                     (                                     "closure of the given graph"                                     );                       
                                                 for                                     (                                     int                                     i = 0; i < V; i++)                       
                                                 {                       
                                                 for                                     (                                     int                                     j = 0; j < V; j++)                       
                                                 {                       
                                                 /* because "i==j means same vertex"                       
                                                 and we can reach same vertex                       
                                                 from same vertex. So, we print 1....                       
                                                 and we have not considered this in                       
                                                 Floyd Warshall Algo. so we need to                       
                                                 make this true by ourself                       
                                                 while printing transitive closure.*/                       
                                                 if                                     (i == j)                       
                                                 printf                                     (                                     "1 "                                     );                       
                                                 else                       
                                                 printf                                     (                                     "%d "                                     , reach[i][j]);                       
                                                 }                       
                                                 printf                                     (                                     ""                                     );                       
                                                 }                       
                         }                       
           
                         // Driver Code                       
                         int                                     main()                       
                         {                       
                                                 /* Let us create the following weighted graph                       
                                                 10                       
                                                 (0)------->(3)                       
                                                 |         /|                       
                                                 5 |          |                       
                                                 |          | 1                       
                                                 |/         |                       
                                                 (1)------->(2)                       
                                                 3           */                       
                                                 int                                     graph[V][V] = { {1, 1, 0, 1},                       
                                                 {0, 1, 1, 0},                       
                                                 {0, 0, 1, 1},                       
                                                 {0, 0, 0, 1}                       
                                                 };                       
           
                                                 // Print the solution                       
                                                 transitiveClosure(graph);                       
                                                 return                                     0;                       
                         }                       

JAVA

                         // Program for transitive closure                       
                         // using Floyd Warshall Algorithm                       
                         import                                     java.util.*;                       
                         import                                     java.lang.*;                       
                         import                                     java.io.*;                       
           
                         class                                     GraphClosure                       
                         {                       
                                                 final                                     static                                     int                                     V =                                     4                                     ;                                     //Number of vertices in a graph                       
           
                                                 // Prints transitive closure of graph[][] using Floyd                       
                                                 // Warshall algorithm                       
                                                 void                                     transitiveClosure(                                     int                                     graph[][])                       
                                                 {                       
                                                 /* reach[][] will be the output matrix that will finally                       
                                                 have the shortest  distances between every pair of                       
                                                 vertices */                       
                                                 int                                     reach[][] =                                     new                                     int                                     [V][V];                       
                                                 int                                     i, j, k;                       
           
                                                 /* Initialize the solution matrix same as input graph                       
                                                 matrix. Or  we can say the initial values of shortest                       
                                                 distances are based  on shortest paths considering                       
                                                 no intermediate vertex. */                       
                                                 for                                     (i =                                     0                                     ; i < V; i++)                       
                                                 for                                     (j =                                     0                                     ; j < V; j++)                       
                                                 reach[i][j] = graph[i][j];                       
           
                                                 /* Add all vertices one by one to the set of intermediate                       
                                                 vertices.                       
                                                 ---> Before start of a iteration, we have reachability                       
                                                 values for all  pairs of vertices such that the                       
                                                 reachability values consider only the vertices in                       
                                                 set {0, 1, 2, .. k-1} as intermediate vertices.                       
                                                 ----> After the end of a iteration, vertex no. k is                       
                                                 added to the set of intermediate vertices and the                       
                                                 set becomes {0, 1, 2, .. k} */                       
                                                 for                                     (k =                                     0                                     ; k < V; k++)                       
                                                 {                       
                                                 // Pick all vertices as source one by one                       
                                                 for                                     (i =                                     0                                     ; i < V; i++)                       
                                                 {                       
                                                 // Pick all vertices as destination for the                       
                                                 // above picked source                       
                                                 for                                     (j =                                     0                                     ; j < V; j++)                       
                                                 {                       
                                                 // If vertex k is on a path from i to j,                       
                                                 // then make sure that the value of reach[i][j] is 1                       
                                                 reach[i][j] = (reach[i][j]!=                                     0                                     ) ||                       
                                                 ((reach[i][k]!=                                     0                                     ) && (reach[k][j]!=                                     0                                     ))?                                     1                                     :                                     0                                     ;                       
                                                 }                       
                                                 }                       
                                                 }                       
           
                                                 // Print the shortest distance matrix                       
                                                 printSolution(reach);                       
                                                 }                       
           
                                                 /* A utility function to print solution */                       
                                                 void                                     printSolution(                                     int                                     reach[][])                       
                                                 {                       
                                                 System.out.println(                                     "Following matrix is transitive closure"                                     +                       
                                                 " of the given graph"                                     );                       
                                                 for                                     (                                     int                                     i =                                     0                                     ; i < V; i++)                       
                                                 {                       
                                                 for                                     (                                     int                                     j =                                     0                                     ; j < V; j++) {                       
                                                 if                                     ( i == j)                       
                                                 System.out.print(                                     "1 "                                     );                       
                                                 else                       
                                                 System.out.print(reach[i][j]+                                     " "                                     );                       
                                                 }                       
                                                 System.out.println();                       
                                                 }                       
                                                 }                       
           
                                                 // Driver Code                       
                                                 public                                     static                                     void                                     main (String[] args)                       
                                                 {                       
                                                 /* Let us create the following weighted graph                       
                                                 10                       
                                                 (0)------->(3)                       
                                                 |         /|                       
                                                 5 |          |                       
                                                 |          | 1                       
                                                 |/        |                       
                                                 (1)------->(2)                       
                                                 3           */                       
           
                                                 /* Let us create the following weighted graph                       
           
                                                 10                       
                                                 (0)------->(3)                       
                                                 |         /|                       
                                                 5 |          |                       
                                                 |          | 1                       
                                                 |/         |                       
                                                 (1)------->(2)                       
                                                 3           */                       
                                                 int                                     graph[][] =                                     new                                     int                                     [][]{ {                                     1                                     ,                                     1                                     ,                                     0                                     ,                                     1                                     },                       
                                                 {                                     0                                     ,                                     1                                     ,                                     1                                     ,                                     0                                     },                       
                                                 {                                     0                                     ,                                     0                                     ,                                     1                                     ,                                     1                                     },                       
                                                 {                                     0                                     ,                                     0                                     ,                                     0                                     ,                                     1                                     }                       
                                                 };                       
           
                                                 // Print the solution                       
                                                 GraphClosure g =                                     new                                     GraphClosure();                       
                                                 g.transitiveClosure(graph);                       
                                                 }                       
                         }                       
                         // This code is contributed by Aakash Hasija                       

Python3

                         # Python program for transitive closure using Floyd Warshall Algorithm                       
                         #Complexity : O(V^3)                       
           
                         from                                     collections                                     import                                     defaultdict                       
           
                         #Class to represent a graph                       
                         class                                     Graph:                       
           
                                                 def                                     __init__(                                     self                                     , vertices):                       
                                                 self                                     .V                                     =                                     vertices                       
           
                                                 # A utility function to print the solution                       
                                                 def                                     printSolution(                                     self                                     , reach):                       
                                                 print                                     (                                     "Following matrix transitive closure of the given graph "                                     )                       
                                                 for                                     i                                     in                                     range                                     (                                     self                                     .V):                       
                                                 for                                     j                                     in                                     range                                     (                                     self                                     .V):                       
                                                 if                                     (i                                     =                                     =                                     j):                       
                                                 print                                     (                                     "%7d	"                                     %                                     (                                     1                                     ),end                                     =                                     " "                                     )                       
                                                 else                                     :                       
                                                 print                                     (                                     "%7d	"                                     %                                     (reach[i][j]),end                                     =                                     " "                                     )                       
                                                 print                                     ()                       
                                   
                                   
                                                 # Prints transitive closure of graph[][] using Floyd Warshall algorithm                       
                                                 def                                     transitiveClosure(                                     self                                     ,graph):                       
                                                 '''reach[][] will be the output matrix that will finally                       
                                                 have reachability values.                       
                                                 Initialize the solution matrix same as input graph matrix'''                       
                                                 reach                                     =                                     [i[:]                                     for                                     i                                     in                                     graph]                       
                                                 '''Add all vertices one by one to the set of intermediate                       
                                                 vertices.                       
                                                 ---> Before start of a iteration, we have reachability value                       
                                                 for all pairs of vertices such that the reachability values                       
                                                 consider only the vertices in set                       
                                                 {0, 1, 2, .. k-1} as intermediate vertices.                       
                                                 ----> After the end of an iteration, vertex no. k is                       
                                                 added to the set of intermediate vertices and the                       
                                                 set becomes {0, 1, 2, .. k}'''                       
                                                 for                                     k                                     in                                     range                                     (                                     self                                     .V):                       
                                   
                                                 # Pick all vertices as source one by one                       
                                                 for                                     i                                     in                                     range                                     (                                     self                                     .V):                       
                                   
                                                 # Pick all vertices as destination for the                       
                                                 # above picked source                       
                                                 for                                     j                                     in                                     range                                     (                                     self                                     .V):                       
                                   
                                                 # If vertex k is on a path from i to j,                       
                                                 # then make sure that the value of reach[i][j] is 1                       
                                                 reach[i][j]                                     =                                     reach[i][j]                                     or                                     (reach[i][k]                                     and                                     reach[k][j])                       
           
                                                 self                                     .printSolution(reach)                       
                                   
                         g                                     =                                     Graph(                                     4                                     )                       
           
                         graph                                     =                                     [[                                     1                                     ,                                     1                                     ,                                     0                                     ,                                     1                                     ],                       
                                                 [                                     0                                     ,                                     1                                     ,                                     1                                     ,                                     0                                     ],                       
                                                 [                                     0                                     ,                                     0                                     ,                                     1                                     ,                                     1                                     ],                       
                                                 [                                     0                                     ,                                     0                                     ,                                     0                                     ,                                     1                                     ]]                       
           
                         #Print the solution                       
                         g.transitiveClosure(graph)                       
           
                         #This code is contributed by Neelam Yadav                       

C#

                         // C# Program for transitive closure                       
                         // using Floyd Warshall Algorithm                       
                         using                                     System;                       
           
                         class                                     GFG                       
                         {                       
                                                 static                                     int                                     V = 4;                                     // Number of vertices in a graph                       
           
                                                 // Prints transitive closure of graph[,]                       
                                                 // using Floyd Warshall algorithm                       
                                                 void                                     transitiveClosure(                                     int                                     [,]graph)                       
                                                 {                       
                                                 /* reach[,] will be the output matrix that                       
                                                 will finally have the shortest distances                       
                                                 between every pair of vertices */                       
                                                 int                                     [,]reach =                                     new                                     int                                     [V, V];                       
                                                 int                                     i, j, k;                       
           
                                                 /* Initialize the solution matrix same as                       
                                                 input graph matrix. Or we can say the                       
                                                 initial values of shortest distances are                       
                                                 based on shortest paths considering no                       
                                                 intermediate vertex. */                       
                                                 for                                     (i = 0; i < V; i++)                       
                                                 for                                     (j = 0; j < V; j++)                       
                                                 reach[i, j] = graph[i, j];                       
           
                                                 /* Add all vertices one by one to the                       
                                                 set of intermediate vertices.                       
                                                 ---> Before start of a iteration, we have                       
                                                 reachability values for all pairs of                       
                                                 vertices such that the reachability                       
                                                 values consider only the vertices in                       
                                                 set {0, 1, 2, .. k-1} as intermediate vertices.                       
                                                 ---> After the end of a iteration, vertex no.                       
                                                 k is added to the set of intermediate                       
                                                 vertices and the set becomes {0, 1, 2, .. k} */                       
                                                 for                                     (k = 0; k < V; k++)                       
                                                 {                       
                                                 // Pick all vertices as source one by one                       
                                                 for                                     (i = 0; i < V; i++)                       
                                                 {                       
                                                 // Pick all vertices as destination                       
                                                 // for the above picked source                       
                                                 for                                     (j = 0; j < V; j++)                       
                                                 {                       
                                                 // If vertex k is on a path from i to j,                       
                                                 // then make sure that the value of                       
                                                 // reach[i,j] is 1                       
                                                 reach[i, j] = (reach[i, j] != 0) ||                       
                                                 ((reach[i, k] != 0) &&                       
                                                 (reach[k, j] != 0)) ? 1 : 0;                       
                                                 }                       
                                                 }                       
                                                 }                       
           
                                                 // Print the shortest distance matrix                       
                                                 printSolution(reach);                       
                                                 }                       
           
                                                 /* A utility function to print solution */                       
                                                 void                                     printSolution(                                     int                                     [,]reach)                       
                                                 {                       
                                                 Console.WriteLine(                                     "Following matrix is transitive"                                     +                       
                                                 " closure of the given graph"                                     );                       
                                                 for                                     (                                     int                                     i = 0; i < V; i++)                       
                                                 {                       
                                                 for                                     (                                     int                                     j = 0; j < V; j++){                       
                                                 if                                     (i == j)                       
                                                 Console.Write(                                     "1 "                                     );                       
                                                 else                       
                                                 Console.Write(reach[i, j] +                                     " "                                     );                       
                                                 }                       
                                                 Console.WriteLine();                       
                                                 }                       
                                                 }                       
           
                                                 // Driver Code                       
                                                 public                                     static                                     void                                     Main (String[] args)                       
                                                 {                       
                                                 /* Let us create the following weighted graph                       
                                                 10                       
                                                 (0)------->(3)                       
                                                 |     /|                       
                                                 5 |     |                       
                                                 |     | 1                       
                                                 |/ |                       
                                                 (1)------->(2)                       
                                                 3     */                       
           
                                                 /* Let us create the following weighted graph                       
           
                                                 10                       
                                                 (0)------->(3)                       
                                                 |     /|                       
                                                 5 |     |                       
                                                 |     | 1                       
                                                 |/     |                       
                                                 (1)------->(2)                       
                                                 3     */                       
                                                 int                                     [,]graph =                                     new                                     int                                     [,]{{1, 1, 0, 1},                       
                                                 {0, 1, 1, 0},                       
                                                 {0, 0, 1, 1},                       
                                                 {0, 0, 0, 1}};                       
           
                                                 // Print the solution                       
                                                 GFG g =                                     new                                     GFG();                       
                                                 g.transitiveClosure(graph);                       
                                                 }                       
                         }                       
           
                         // This code is contributed by 29AjayKumar                       

Javascript

                         <script>                       
                                                 // JavaScript Program for transitive closure                       
                                                 // using Floyd Warshall Algorithm                       
                                                 var                                     V = 4;                                     // Number of vertices in a graph                       
           
                                                 // Prints transitive closure of graph[,]                       
                                                 // using Floyd Warshall algorithm                       
                                                 function                                     transitiveClosure(graph) {                       
                                                 /* reach[,] will be the output matrix that                       
                                                 will finally have the shortest distances                       
                                                 between every pair of vertices */                       
                                                 var                                     reach = Array.from(Array(V), () =>                                     new                                     Array(V));                       
                                                 var                                     i, j, k;                       
           
                                                 /* Initialize the solution matrix same as                       
                                                 input graph matrix. Or we can say the                       
                                                 initial values of shortest distances are                       
                                                 based on shortest paths considering no                       
                                                 intermediate vertex. */                       
                                                 for                                     (i = 0; i < V; i++)                       
                                                 for                                     (j = 0; j < V; j++) reach[i][j] = graph[i][j];                       
           
                                                 /* Add all vertices one by one to the                       
                                                 set of intermediate vertices.                       
                                                 ---> Before start of a iteration, we have                       
                                                 reachability values for all pairs of                       
                                                 vertices such that the reachability                       
                                                 values consider only the vertices in                       
                                                 set {0, 1, 2, .. k-1} as intermediate vertices.                       
                                                 ---> After the end of a iteration, vertex no.                       
                                                 k is added to the set of intermediate                       
                                                 vertices and the set becomes {0, 1, 2, .. k} */                       
                                                 for                                     (k = 0; k < V; k++) {                       
                                                 // Pick all vertices as source one by one                       
                                                 for                                     (i = 0; i < V; i++) {                       
                                                 // Pick all vertices as destination                       
                                                 // for the above picked source                       
                                                 for                                     (j = 0; j < V; j++) {                       
                                                 // If vertex k is on a path from i to j,                       
                                                 // then make sure that the value of                       
                                                 // reach[i,j] is 1                       
                                                 reach[i][j] =                       
                                                 reach[i][j] != 0 || (reach[i][k] != 0 && reach[k][j] != 0)                       
                                                 ? 1                       
                                                 : 0;                       
                                                 }                       
                                                 }                       
                                                 }                       
           
                                                 // Print the shortest distance matrix                       
                                                 printSolution(reach);                       
                                                 }                       
           
                                                 /* A utility function to print solution */                       
                                                 function                                     printSolution(reach) {                       
                                                 document.write(                       
                                                 "Following matrix is transitive"                                     +                                     " closure of the given graph <br>"                       
                                                 );                       
                                                 for                                     (                                     var                                     i = 0; i < V; i++) {                       
                                                 for                                     (                                     var                                     j = 0; j < V; j++) {                       
                                                 if                                     (i == j) document.write(                                     "1 "                                     );                       
                                                 else                                     document.write(reach[i][j] +                                     " "                                     );                       
                                                 }                       
                                                 document.write(                                     "<br>"                                     );                       
                                                 }                       
                                                 }                       
           
                                                 // Driver Code                       
                                                 /* Let us create the following weighted graph                       
                                                 10                       
                                                 (0)------->(3)                       
                                                 |     /|                       
                                                 5 |     |                       
                                                 |     | 1                       
                                                 |/ |                       
                                                 (1)------->(2)                       
                                                 3     */                       
           
                                                 /* Let us create the following weighted graph                       
           
                                                 10                       
                                                 (0)------->(3)                       
                                                 |     /|                       
                                                 5 |     |                       
                                                 |     | 1                       
                                                 |/     |                       
                                                 (1)------->(2)                       
                                                 3     */                       
                                                 var                                     graph = [                       
                                                 [1, 1, 0, 1],                       
                                                 [0, 1, 1, 0],                       
                                                 [0, 0, 1, 1],                       
                                                 [0, 0, 0, 1],                       
                                                 ];                       
           
                                                 // Print the solution                       
           
                                                 transitiveClosure(graph);                       
                                   
                                                 // This code is contributed by rdtank.                       
                                                 </script>                       

输出

Following matrix is transitiveclosure of the given graph1 1 1 1 0 1 1 1 0 0 1 1 0 0 0 1

时间复杂性： O（V） ^3. )其中V是给定图形中的顶点数。请参见下面的帖子了解O（V） ^2. )解决方案。使用DFS的图的传递闭包 参考资料： Clifford Stein、Thomas H.Cormen、Charles E.Leiserson、Ronald L。如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请写下评论。

文章版权归作者所有，未经允许请勿转载。

THE END

技术文章