给定一个二叉搜索树(BST)和一个范围[min,max],删除给定范围之外的所有密钥。修改后的树也应该是BST。例如,考虑下面的BST和范围[-10, 13 ]。
null
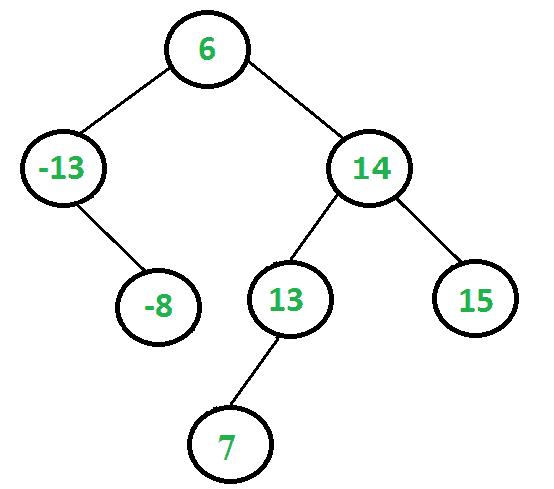
给定的树应更改为以下内容。请注意,范围[-10,13]之外的所有键都将被删除,修改后的树为BST。
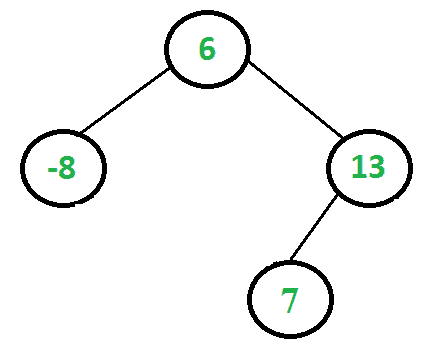
每个节点都有两种可能的情况。 1) 节点的密钥不在给定范围内。本案例有两个子案例。 ……. (a) 节点的键小于最小值。 ……. b) 节点的键大于最大值。 2) 节点的键在范围内。 我们不需要为案例2做任何事情。在案例1中,我们需要删除该节点并更改以该节点为根的子树的根。
我们的想法是以后期订购的方式修复这棵树。当我们访问一个节点时,我们要确保它的左、右子树已经固定。在案例1中。a) ,我们只需删除根并将正确的子树作为新根返回。在案例1中。b) ,我们移除根并将左子树作为新根返回。
以下是上述方法的实现。
C++
// A C++ program to remove BST keys outside the given range #include<bits/stdc++.h> using namespace std; // A BST node has key, and left and right pointers struct node { int key; struct node *left; struct node *right; }; // Removes all nodes having value outside the given range and returns the root // of modified tree node* removeOutsideRange(node *root, int min, int max) { // Base Case if (root == NULL) return NULL; // First fix the left and right subtrees of root root->left = removeOutsideRange(root->left, min, max); root->right = removeOutsideRange(root->right, min, max); // Now fix the root. There are 2 possible cases for root // 1.a) Root's key is smaller than min value (root is not in range) if (root->key < min) { node *rChild = root->right; delete root; return rChild; } // 1.b) Root's key is greater than max value (root is not in range) if (root->key > max) { node *lChild = root->left; delete root; return lChild; } // 2. Root is in range return root; } // A utility function to create a new BST node with key as given num node* newNode( int num) { node* temp = new node; temp->key = num; temp->left = temp->right = NULL; return temp; } // A utility function to insert a given key to BST node* insert(node* root, int key) { if (root == NULL) return newNode(key); if (root->key > key) root->left = insert(root->left, key); else root->right = insert(root->right, key); return root; } // Utility function to traverse the binary tree after conversion void inorderTraversal(node* root) { if (root) { inorderTraversal( root->left ); cout << root->key << " " ; inorderTraversal( root->right ); } } // Driver program to test above functions int main() { node* root = NULL; root = insert(root, 6); root = insert(root, -13); root = insert(root, 14); root = insert(root, -8); root = insert(root, 15); root = insert(root, 13); root = insert(root, 7); cout << "Inorder traversal of the given tree is: " ; inorderTraversal(root); root = removeOutsideRange(root, -10, 13); cout << "Inorder traversal of the modified tree is: " ; inorderTraversal(root); return 0; } |
JAVA
// A Java program to remove BST // keys outside the given range import java.math.BigDecimal; import java.util.ArrayList; import java.util.Arrays; import java.util.List; import java.util.Scanner; class Node { int key; Node left; Node right; } class GFG { // Removes all nodes having value // outside the given range and // returns the root of modified tree private static Node removeOutsideRange(Node root, int min, int max) { // BASE CASE if (root == null ) { return null ; } // FIRST FIX THE LEFT AND // RIGHT SUBTREE OF ROOT root.left = removeOutsideRange(root.left, min, max); root.right = removeOutsideRange(root.right, min, max); // NOW FIX THE ROOT. THERE ARE // TWO POSSIBLE CASES FOR THE ROOT // 1. a) Root's key is smaller than // min value(root is not in range) if (root.key < min) { Node rchild = root.right; root = null ; return rchild; } // 1. b) Root's key is greater than // max value (Root is not in range) if (root.key > max) { Node lchild = root.left; root = null ; return lchild; } // 2. Root in range return root; } public static Node newNode( int num) { Node temp = new Node(); temp.key = num; temp.left = null ; temp.right = null ; return temp; } public static Node insert(Node root, int key) { if (root == null ) { return newNode(key); } if (root.key > key) { root.left = insert(root.left, key); } else { root.right = insert(root.right, key); } return root; } private static void inorderTraversal(Node root) { if (root != null ) { inorderTraversal(root.left); System.out.print(root.key + " " ); inorderTraversal(root.right); } } // Driver code public static void main(String[] args) { Node root = null ; root = insert(root, 6 ); root = insert(root, - 13 ); root = insert(root, 14 ); root = insert(root, - 8 ); root = insert(root, 15 ); root = insert(root, 13 ); root = insert(root, 7 ); System.out.print( "Inorder Traversal of " + "the given tree is: " ); inorderTraversal(root); root = removeOutsideRange(root, - 10 , 13 ); System.out.print( "Inorder traversal of " + "the modified tree: " ); inorderTraversal(root); } } // This code is contributed // by Divya |
Python3
# Python3 program to remove BST keys # outside the given range # A BST node has key, and left and right # pointers. A utility function to create # a new BST node with key as given num class newNode: # Constructor to create a new node def __init__( self , data): self .key = data self .left = None self .right = None # Removes all nodes having value outside # the given range and returns the root # of modified tree def removeOutsideRange(root, Min , Max ): # Base Case if root = = None : return None # First fix the left and right # subtrees of root root.left = removeOutsideRange(root.left, Min , Max ) root.right = removeOutsideRange(root.right, Min , Max ) # Now fix the root. There are 2 # possible cases for root # 1.a) Root's key is smaller than # min value (root is not in range) if root.key < Min : rChild = root.right return rChild # 1.b) Root's key is greater than max # value (root is not in range) if root.key > Max : lChild = root.left return lChild # 2. Root is in range return root # A utility function to insert a given # key to BST def insert(root, key): if root = = None : return newNode(key) if root.key > key: root.left = insert(root.left, key) else : root.right = insert(root.right, key) return root # Utility function to traverse the binary # tree after conversion def inorderTraversal(root): if root: inorderTraversal( root.left) print (root.key, end = " " ) inorderTraversal( root.right) # Driver Code if __name__ = = '__main__' : root = None root = insert(root, 6 ) root = insert(root, - 13 ) root = insert(root, 14 ) root = insert(root, - 8 ) root = insert(root, 15 ) root = insert(root, 13 ) root = insert(root, 7 ) print ( "Inorder traversal of the given tree is:" , end = " " ) inorderTraversal(root) root = removeOutsideRange(root, - 10 , 13 ) print () print ( "Inorder traversal of the modified tree is:" , end = " " ) inorderTraversal(root) # This code is contributed by PranchalK |
C#
// A C# program to remove BST // keys outside the given range using System; public class Node { public int key; public Node left; public Node right; } public class GFG { // Removes all nodes having value // outside the given range and // returns the root of modified tree private static Node removeOutsideRange(Node root, int min, int max) { // BASE CASE if (root == null ) { return null ; } // FIRST FIX THE LEFT AND // RIGHT SUBTREE OF ROOT root.left = removeOutsideRange(root.left, min, max); root.right = removeOutsideRange(root.right, min, max); // NOW FIX THE ROOT. THERE ARE // TWO POSSIBLE CASES FOR THE ROOT // 1. a) Root's key is smaller than // min value(root is not in range) if (root.key < min) { Node rchild = root.right; root = null ; return rchild; } // 1. b) Root's key is greater than // max value (Root is not in range) if (root.key > max) { Node lchild = root.left; root = null ; return lchild; } // 2. Root in range return root; } public static Node newNode( int num) { Node temp = new Node(); temp.key = num; temp.left = null ; temp.right = null ; return temp; } public static Node insert(Node root, int key) { if (root == null ) { return newNode(key); } if (root.key > key) { root.left = insert(root.left, key); } else { root.right = insert(root.right, key); } return root; } private static void inorderTraversal(Node root) { if (root != null ) { inorderTraversal(root.left); Console.Write(root.key + " " ); inorderTraversal(root.right); } } // Driver code public static void Main(String[] args) { Node root = null ; root = insert(root, 6); root = insert(root, -13); root = insert(root, 14); root = insert(root, -8); root = insert(root, 15); root = insert(root, 13); root = insert(root, 7); Console.Write( "Inorder Traversal of " + "the given tree is: " ); inorderTraversal(root); root = removeOutsideRange(root, -10, 13); Console.Write( "Inorder traversal of " + "the modified tree: " ); inorderTraversal(root); } } // This code has been contributed // by PrinciRaj1992 |
Javascript
<script> // A JavaScript program to remove BST // keys outside the given range class Node { constructor() { this .key = 0; this .left = null ; this .right = null ; } } // Removes all nodes having value // outside the given range and // returns the root of modified tree function removeOutsideRange(root , min , max) { // BASE CASE if (root == null ) { return null ; } // FIRST FIX THE LEFT AND // RIGHT SUBTREE OF ROOT root.left = removeOutsideRange(root.left, min, max); root.right = removeOutsideRange(root.right, min, max); // NOW FIX THE ROOT. THERE ARE // TWO POSSIBLE CASES FOR THE ROOT // 1. a) Root's key is smaller than // min value(root is not in range) if (root.key < min) { var rchild = root.right; root = null ; return rchild; } // 1. b) Root's key is greater than // max value (Root is not in range) if (root.key > max) { var lchild = root.left; root = null ; return lchild; } // 2. Root in range return root; } function newNode(num) { var temp = new Node(); temp.key = num; temp.left = null ; temp.right = null ; return temp; } function insert(root , key) { if (root == null ) { return newNode(key); } if (root.key > key) { root.left = insert(root.left, key); } else { root.right = insert(root.right, key); } return root; } function inorderTraversal(root) { if (root != null ) { inorderTraversal(root.left); document.write(root.key + " " ); inorderTraversal(root.right); } } // Driver code var root = null ; root = insert(root, 6); root = insert(root, -13); root = insert(root, 14); root = insert(root, -8); root = insert(root, 15); root = insert(root, 13); root = insert(root, 7); document.write( "Inorder Traversal of " + "the given tree is: " ); inorderTraversal(root); root = removeOutsideRange(root, -10, 13); document.write( "<br/>Inorder traversal of " + "the modified tree: " ); inorderTraversal(root); // This code is contributed by todaysgaurav </script> |
输出:
Inorder traversal of the given tree is: -13 -8 6 7 13 14 15Inorder traversal of the modified tree is: -8 6 7 13
时间复杂性: O(n),其中n是给定BST中的节点数。
如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写下评论。
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



