在 以前的职位 ,我们引入了B-树。我们还讨论了search()和traverse()函数。 本文将讨论insert()操作。新密钥始终插入到叶节点。让要插入的键为k。像BST一样,我们从根开始向下遍历,直到到达叶节点。一旦我们到达一个叶节点,我们就将密钥插入该叶节点。与BST不同,我们对节点可以包含的键的数量有一个预定义的范围。因此,在向节点插入密钥之前,我们要确保节点有额外的空间。
在插入密钥之前,如何确保节点具有密钥可用的空间? 我们使用一个名为splitChild()的操作来拆分节点的子节点。请参见下图以了解拆分。在下图中,x的子y被拆分为两个节点y和z。请注意,splitChild操作会向上移动一个键,这就是B树长大的原因,而BST会向下生长。

如上所述,要插入一个新密钥,我们从根到叶。在向下遍历节点之前,我们首先检查节点是否已满。如果节点已满,我们将其拆分以创建空间。下面是完整的算法。
插入 1) 将x初始化为根。 2) 虽然x不是叶子,但要做到以下几点 .. (a) 找到下一步要遍历的x的子对象。让这孩子安静点。 .. b) 如果y未满,则将x更改为指向y。 .. c) 如果y已满,将其拆分,并将x更改为指向y的两个部分之一。如果k小于y中的中间关键点,则将x设置为y的第一部分。否则设置为y的第二部分。拆分y时,将关键点从y移动到其父x。 3) 当x为leaf时,步骤2中的循环停止。x必须有空间容纳1个额外的密钥,因为我们已经提前拆分了所有节点。所以简单地把k插入x。
请注意,该算法遵循Cormen手册。它实际上是一种主动插入算法,在进入节点之前,如果节点已满,我们将其拆分。之前拆分的优点是,我们不会遍历一个节点两次。如果我们在进入一个节点之前不拆分它,并且只在插入一个新密钥时拆分它(被动),那么我们可能会再次从叶到根遍历所有节点。当从根到叶的路径上的所有节点都已满时,就会发生这种情况。因此,当我们来到叶节点时,我们将其拆分并向上移动一个关键点。向上移动关键点将导致父节点分裂(因为父节点已满)。这种级联效应在这种主动插入算法中从未发生过。不过,这种主动插入有一个缺点,我们可能会进行不必要的拆分。
让我们用一个最小度为3的示例树和一个初始空B树中的整数序列10、20、30、40、50、60、70、80和90来理解该算法。 最初root为NULL。让我们先插入10。

现在让我们插入20、30、40和50。它们都将插入根目录中,因为节点可以容纳的最大密钥数为2*t–1,即5。
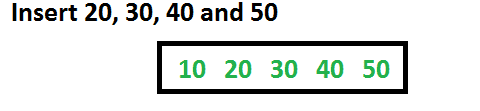
现在让我们插入60。由于根节点已满,它将首先拆分为两个,然后将60个节点插入相应的子节点。
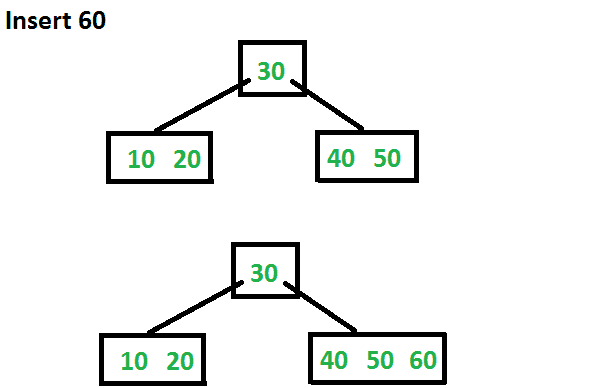
现在让我们插入70和80。这些新键将被插入到相应的叶中,而不进行任何拆分。
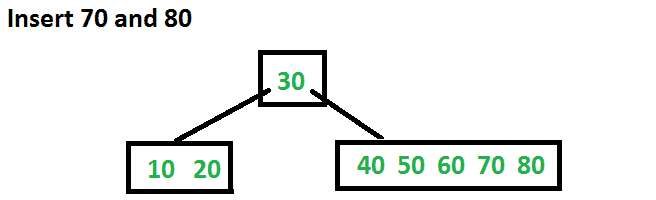
现在让我们插入90。此插入将导致拆分。中键将转到父键。
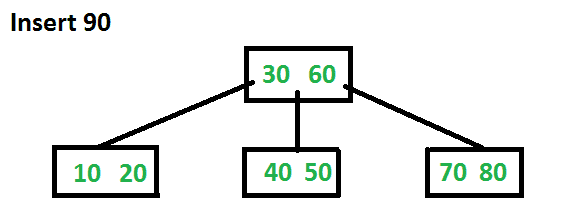
下面是C++实现上述主动算法。
C++
// C++ program for B-Tree insertion #include<iostream> using namespace std; // A BTree node class BTreeNode { int *keys; // An array of keys int t; // Minimum degree (defines the range for number of keys) BTreeNode **C; // An array of child pointers int n; // Current number of keys bool leaf; // Is true when node is leaf. Otherwise false public : BTreeNode( int _t, bool _leaf); // Constructor // A utility function to insert a new key in the subtree rooted with // this node. The assumption is, the node must be non-full when this // function is called void insertNonFull( int k); // A utility function to split the child y of this node. i is index of y in // child array C[]. The Child y must be full when this function is called void splitChild( int i, BTreeNode *y); // A function to traverse all nodes in a subtree rooted with this node void traverse(); // A function to search a key in the subtree rooted with this node. BTreeNode *search( int k); // returns NULL if k is not present. // Make BTree friend of this so that we can access private members of this // class in BTree functions friend class BTree; }; // A BTree class BTree { BTreeNode *root; // Pointer to root node int t; // Minimum degree public : // Constructor (Initializes tree as empty) BTree( int _t) { root = NULL; t = _t; } // function to traverse the tree void traverse() { if (root != NULL) root->traverse(); } // function to search a key in this tree BTreeNode* search( int k) { return (root == NULL)? NULL : root->search(k); } // The main function that inserts a new key in this B-Tree void insert( int k); }; // Constructor for BTreeNode class BTreeNode::BTreeNode( int t1, bool leaf1) { // Copy the given minimum degree and leaf property t = t1; leaf = leaf1; // Allocate memory for maximum number of possible keys // and child pointers keys = new int [2*t-1]; C = new BTreeNode *[2*t]; // Initialize the number of keys as 0 n = 0; } // Function to traverse all nodes in a subtree rooted with this node void BTreeNode::traverse() { // There are n keys and n+1 children, traverse through n keys // and first n children int i; for (i = 0; i < n; i++) { // If this is not leaf, then before printing key[i], // traverse the subtree rooted with child C[i]. if (leaf == false ) C[i]->traverse(); cout << " " << keys[i]; } // Print the subtree rooted with last child if (leaf == false ) C[i]->traverse(); } // Function to search key k in subtree rooted with this node BTreeNode *BTreeNode::search( int k) { // Find the first key greater than or equal to k int i = 0; while (i < n && k > keys[i]) i++; // If the found key is equal to k, return this node if (keys[i] == k) return this ; // If key is not found here and this is a leaf node if (leaf == true ) return NULL; // Go to the appropriate child return C[i]->search(k); } // The main function that inserts a new key in this B-Tree void BTree::insert( int k) { // If tree is empty if (root == NULL) { // Allocate memory for root root = new BTreeNode(t, true ); root->keys[0] = k; // Insert key root->n = 1; // Update number of keys in root } else // If tree is not empty { // If root is full, then tree grows in height if (root->n == 2*t-1) { // Allocate memory for new root BTreeNode *s = new BTreeNode(t, false ); // Make old root as child of new root s->C[0] = root; // Split the old root and move 1 key to the new root s->splitChild(0, root); // New root has two children now. Decide which of the // two children is going to have new key int i = 0; if (s->keys[0] < k) i++; s->C[i]->insertNonFull(k); // Change root root = s; } else // If root is not full, call insertNonFull for root root->insertNonFull(k); } } // A utility function to insert a new key in this node // The assumption is, the node must be non-full when this // function is called void BTreeNode::insertNonFull( int k) { // Initialize index as index of rightmost element int i = n-1; // If this is a leaf node if (leaf == true ) { // The following loop does two things // a) Finds the location of new key to be inserted // b) Moves all greater keys to one place ahead while (i >= 0 && keys[i] > k) { keys[i+1] = keys[i]; i--; } // Insert the new key at found location keys[i+1] = k; n = n+1; } else // If this node is not leaf { // Find the child which is going to have the new key while (i >= 0 && keys[i] > k) i--; // See if the found child is full if (C[i+1]->n == 2*t-1) { // If the child is full, then split it splitChild(i+1, C[i+1]); // After split, the middle key of C[i] goes up and // C[i] is splitted into two. See which of the two // is going to have the new key if (keys[i+1] < k) i++; } C[i+1]->insertNonFull(k); } } // A utility function to split the child y of this node // Note that y must be full when this function is called void BTreeNode::splitChild( int i, BTreeNode *y) { // Create a new node which is going to store (t-1) keys // of y BTreeNode *z = new BTreeNode(y->t, y->leaf); z->n = t - 1; // Copy the last (t-1) keys of y to z for ( int j = 0; j < t-1; j++) z->keys[j] = y->keys[j+t]; // Copy the last t children of y to z if (y->leaf == false ) { for ( int j = 0; j < t; j++) z->C[j] = y->C[j+t]; } // Reduce the number of keys in y y->n = t - 1; // Since this node is going to have a new child, // create space of new child for ( int j = n; j >= i+1; j--) C[j+1] = C[j]; // Link the new child to this node C[i+1] = z; // A key of y will move to this node. Find the location of // new key and move all greater keys one space ahead for ( int j = n-1; j >= i; j--) keys[j+1] = keys[j]; // Copy the middle key of y to this node keys[i] = y->keys[t-1]; // Increment count of keys in this node n = n + 1; } // Driver program to test above functions int main() { BTree t(3); // A B-Tree with minimum degree 3 t.insert(10); t.insert(20); t.insert(5); t.insert(6); t.insert(12); t.insert(30); t.insert(7); t.insert(17); cout << "Traversal of the constructed tree is " ; t.traverse(); int k = 6; (t.search(k) != NULL)? cout << "Present" : cout << "Not Present" ; k = 15; (t.search(k) != NULL)? cout << "Present" : cout << "Not Present" ; return 0; } |
输出:
Traversal of the constructed tree is 5 6 7 10 12 17 20 30PresentNot Present
参考资料: 算法导论第三版由Clifford Stein、Thomas H.Cormen、Charles E.Leiserson、Ronald L.Rivest编写 http://www.cs.utexas.edu/users/djimenez/utsa/cs3343/lecture17.html 如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写下评论。


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



