给出完整二叉树的链表表示,构造二叉树。一个完整的二叉树可以用以下方法表示在一个数组中。 如果根节点存储在索引i处,则其左、右子节点分别存储在索引2*i+1、2*i+2处。 假设树以同样的方式由链表表示,我们如何将其转换为二叉树的正常链表表示,其中每个节点都有数据、左指针和右指针?在链表表示法中,除非遍历链表,否则无法直接访问当前节点的子节点。
null
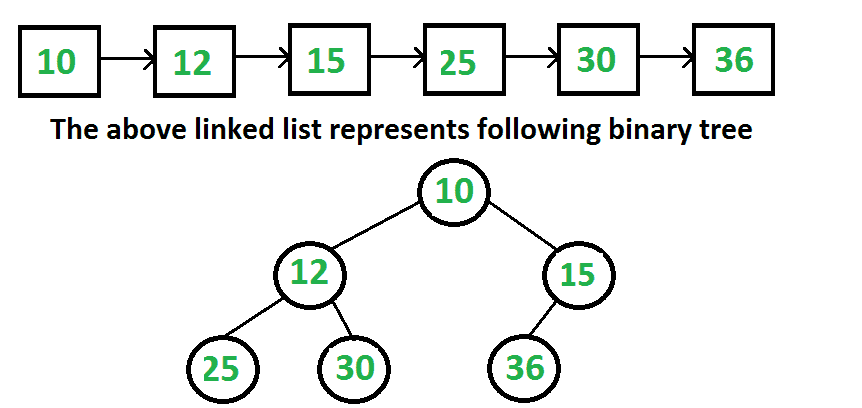
我们主要是以顺序存取的形式给出级序遍历。我们知道链表的头总是树的根。我们把第一个节点作为根,我们也知道接下来的两个节点是根的左和右子节点。所以我们知道部分二叉树。其思想是使用队列对部分构建的二叉树进行水平顺序遍历,同时遍历链表。在每一步中,我们从队列中取出父节点,将链表的下两个节点作为父节点的子节点,并将下两个节点排队。 1. 创建一个空队列。 2. 将列表的第一个节点设为根节点,并将其排入队列。 3. 在列表结束之前,请执行以下操作。 ……… A. 从队列中退出一个节点。这是当前的父级。 ……… B 遍历列表中的两个节点,将它们添加为当前父节点的子节点。 ……… C 将两个节点排队。 下面是在C++中实现相同代码的代码。
C++
// C++ program to create a Complete Binary tree from its Linked List // Representation #include <iostream> #include <string> #include <queue> using namespace std; // Linked list node struct ListNode { int data; ListNode* next; }; // Binary tree node structure struct BinaryTreeNode { int data; BinaryTreeNode *left, *right; }; // Function to insert a node at the beginning of the Linked List void push( struct ListNode** head_ref, int new_data) { // allocate node and assign data struct ListNode* new_node = new ListNode; new_node->data = new_data; // link the old list off the new node new_node->next = (*head_ref); // move the head to point to the new node (*head_ref) = new_node; } // method to create a new binary tree node from the given data BinaryTreeNode* newBinaryTreeNode( int data) { BinaryTreeNode *temp = new BinaryTreeNode; temp->data = data; temp->left = temp->right = NULL; return temp; } // converts a given linked list representing a complete binary tree into the // linked representation of binary tree. void convertList2Binary(ListNode *head, BinaryTreeNode* &root) { // queue to store the parent nodes queue<BinaryTreeNode *> q; // Base Case if (head == NULL) { root = NULL; // Note that root is passed by reference return ; } // 1.) The first node is always the root node, and add it to the queue root = newBinaryTreeNode(head->data); q.push(root); // advance the pointer to the next node head = head->next; // until the end of linked list is reached, do the following steps while (head) { // 2.a) take the parent node from the q and remove it from q BinaryTreeNode* parent = q.front(); q.pop(); // 2.c) take next two nodes from the linked list. We will add // them as children of the current parent node in step 2.b. Push them // into the queue so that they will be parents to the future nodes BinaryTreeNode *leftChild = NULL, *rightChild = NULL; leftChild = newBinaryTreeNode(head->data); q.push(leftChild); head = head->next; if (head) { rightChild = newBinaryTreeNode(head->data); q.push(rightChild); head = head->next; } // 2.b) assign the left and right children of parent parent->left = leftChild; parent->right = rightChild; } } // Utility function to traverse the binary tree after conversion void inorderTraversal(BinaryTreeNode* root) { if (root) { inorderTraversal( root->left ); cout << root->data << " " ; inorderTraversal( root->right ); } } // Driver program to test above functions int main() { // create a linked list shown in above diagram struct ListNode* head = NULL; push(&head, 36); /* Last node of Linked List */ push(&head, 30); push(&head, 25); push(&head, 15); push(&head, 12); push(&head, 10); /* First node of Linked List */ BinaryTreeNode *root; convertList2Binary(head, root); cout << "Inorder Traversal of the constructed Binary Tree is: " ; inorderTraversal(root); return 0; } |
JAVA
// Java program to create complete Binary Tree from its Linked List // representation // importing necessary classes import java.util.*; // A linked list node class ListNode { int data; ListNode next; ListNode( int d) { data = d; next = null ; } } // A binary tree node class BinaryTreeNode { int data; BinaryTreeNode left, right = null ; BinaryTreeNode( int data) { this .data = data; left = right = null ; } } class BinaryTree { ListNode head; BinaryTreeNode root; // Function to insert a node at the beginning of // the Linked List void push( int new_data) { // allocate node and assign data ListNode new_node = new ListNode(new_data); // link the old list off the new node new_node.next = head; // move the head to point to the new node head = new_node; } // converts a given linked list representing a // complete binary tree into the linked // representation of binary tree. BinaryTreeNode convertList2Binary(BinaryTreeNode node) { // queue to store the parent nodes Queue<BinaryTreeNode> q = new LinkedList<BinaryTreeNode>(); // Base Case if (head == null ) { node = null ; return null ; } // 1.) The first node is always the root node, and // add it to the queue node = new BinaryTreeNode(head.data); q.add(node); // advance the pointer to the next node head = head.next; // until the end of linked list is reached, do the // following steps while (head != null ) { // 2.a) take the parent node from the q and // remove it from q BinaryTreeNode parent = q.peek(); // 2.c) take next two nodes from the linked list. // We will add them as children of the current // parent node in step 2.b. Push them into the // queue so that they will be parents to the // future nodes BinaryTreeNode leftChild = null , rightChild = null ; leftChild = new BinaryTreeNode(head.data); q.add(leftChild); head = head.next; if (head != null ) { rightChild = new BinaryTreeNode(head.data); q.add(rightChild); head = head.next; } // 2.b) assign the left and right children of // parent parent.left = leftChild; parent.right = rightChild; } return node; } // Utility function to traverse the binary tree // after conversion void inorderTraversal(BinaryTreeNode node) { if (node != null ) { inorderTraversal(node.left); System.out.print(node.data + " " ); inorderTraversal(node.right); } } // Driver program to test above functions public static void main(String[] args) { BinaryTree tree = new BinaryTree(); tree.push( 36 ); /* Last node of Linked List */ tree.push( 30 ); tree.push( 25 ); tree.push( 15 ); tree.push( 12 ); tree.push( 10 ); /* First node of Linked List */ BinaryTreeNode node = tree.convertList2Binary(tree.root); System.out.println( "Inorder Traversal of the" + " constructed Binary Tree is:" ); tree.inorderTraversal(node); } } // This code has been contributed by Mayank Jaiswal |
Python3
# Python program to create a Complete Binary Tree from # its linked list representation # Linked List node class ListNode: # Constructor to create a new node def __init__( self , data): self .data = data self . next = None # Binary Tree Node structure class BinaryTreeNode: # Constructor to create a new node def __init__( self , data): self .data = data self .left = None self .right = None # Class to convert the linked list to Binary Tree class Conversion: # Constructor for storing head of linked list # and root for the Binary Tree def __init__( self , data = None ): self .head = None self .root = None def push( self , new_data): # Creating a new linked list node and storing data new_node = ListNode(new_data) # Make next of new node as head new_node. next = self .head # Move the head to point to new node self .head = new_node def convertList2Binary( self ): # Queue to store the parent nodes q = [] # Base Case if self .head is None : self .root = None return # 1.) The first node is always the root node, # and add it to the queue self .root = BinaryTreeNode( self .head.data) q.append( self .root) # Advance the pointer to the next node self .head = self .head. next # Until the end of linked list is reached, do: while ( self .head): # 2.a) Take the parent node from the q and # and remove it from q parent = q.pop( 0 ) # Front of queue # 2.c) Take next two nodes from the linked list. # We will add them as children of the current # parent node in step 2.b. # Push them into the queue so that they will be # parent to the future node leftChild = None rightChild = None leftChild = BinaryTreeNode( self .head.data) q.append(leftChild) self .head = self .head. next if ( self .head): rightChild = BinaryTreeNode( self .head.data) q.append(rightChild) self .head = self .head. next #2.b) Assign the left and right children of parent parent.left = leftChild parent.right = rightChild def inorderTraversal( self , root): if (root): self .inorderTraversal(root.left) print (root.data,end = " " ) self .inorderTraversal(root.right) # Driver Program to test above function # Object of conversion class conv = Conversion() conv.push( 36 ) conv.push( 30 ) conv.push( 25 ) conv.push( 15 ) conv.push( 12 ) conv.push( 10 ) conv.convertList2Binary() print ( "Inorder Traversal of the constructed Binary Tree is:" ) conv.inorderTraversal(conv.root) # This code is contributed by Nikhil Kumar Singh(nickzuck_007) |
C#
// C# program to create complete // Binary Tree from its Linked List // representation // importing necessary classes using System; using System.Collections.Generic; // A linked list node public class ListNode { public int data; public ListNode next; public ListNode( int d) { data = d; next = null ; } } // A binary tree node public class BinaryTreeNode { public int data; public BinaryTreeNode left, right = null ; public BinaryTreeNode( int data) { this .data = data; left = right = null ; } } public class BinaryTree { ListNode head; BinaryTreeNode root; // Function to insert a node at // the beginning of the Linked List void push( int new_data) { // allocate node and assign data ListNode new_node = new ListNode(new_data); // link the old list off the new node new_node.next = head; // move the head to point to the new node head = new_node; } // converts a given linked list representing a // complete binary tree into the linked // representation of binary tree. BinaryTreeNode convertList2Binary(BinaryTreeNode node) { // queue to store the parent nodes Queue<BinaryTreeNode> q = new Queue<BinaryTreeNode>(); // Base Case if (head == null ) { node = null ; return null ; } // 1.) The first node is always the root node, and // add it to the queue node = new BinaryTreeNode(head.data); q.Enqueue(node); // advance the pointer to the next node head = head.next; // until the end of linked list is reached, // do the following steps while (head != null ) { // 2.a) take the parent node from the q and // remove it from q BinaryTreeNode parent = q.Peek(); BinaryTreeNode pp = q.Dequeue(); // 2.c) take next two nodes from the linked list. // We will add them as children of the current // parent node in step 2.b. Push them into the // queue so that they will be parents to the // future nodes BinaryTreeNode leftChild = null , rightChild = null ; leftChild = new BinaryTreeNode(head.data); q.Enqueue(leftChild); head = head.next; if (head != null ) { rightChild = new BinaryTreeNode(head.data); q.Enqueue(rightChild); head = head.next; } // 2.b) assign the left and right children of // parent parent.left = leftChild; parent.right = rightChild; } return node; } // Utility function to traverse the binary tree // after conversion void inorderTraversal(BinaryTreeNode node) { if (node != null ) { inorderTraversal(node.left); Console.Write(node.data + " " ); inorderTraversal(node.right); } } // Driver code public static void Main() { BinaryTree tree = new BinaryTree(); /* Last node of Linked List */ tree.push(36); tree.push(30); tree.push(25); tree.push(15); tree.push(12); /* First node of Linked List */ tree.push(10); BinaryTreeNode node = tree.convertList2Binary(tree.root); Console.WriteLine( "Inorder Traversal of the" + " constructed Binary Tree is:" ); tree.inorderTraversal(node); } } /* This code is contributed PrinciRaj1992 */ |
Javascript
<script> // JavaScript program to create complete // Binary Tree from its Linked List // representation // importing necessary classes // A linked list node class ListNode { constructor(d) { this .data = d; this .next = null ; } } // A binary tree node class BinaryTreeNode { constructor(data) { this .data = data; this .left = null ; this .right = null ; } } class BinaryTree { constructor() { this .head = null ; this .root = null ; } // Function to insert a node at // the beginning of the Linked List push(new_data) { // allocate node and assign data var new_node = new ListNode(new_data); // link the old list off the new node new_node.next = this .head; // move the head to point to the new node this .head = new_node; } // converts a given linked list representing a // complete binary tree into the linked // representation of binary tree. convertList2Binary(node) { // queue to store the parent nodes var q = []; // Base Case if ( this .head == null ) { node = null ; return null ; } // 1.) The first node is always the root node, and // add it to the queue node = new BinaryTreeNode( this .head.data); q.push(node); // advance the pointer to the next node this .head = this .head.next; // until the end of linked list is reached, // do the following steps while ( this .head != null ) { // 2.a) take the parent node from the q and // remove it from q var parent = q.shift(); // 2.c) take next two nodes from the linked list. // We will add them as children of the current // parent node in step 2.b. Push them into the // queue so that they will be parents to the // future nodes var leftChild = null , rightChild = null ; leftChild = new BinaryTreeNode( this .head.data); q.push(leftChild); this .head = this .head.next; if ( this .head != null ) { rightChild = new BinaryTreeNode( this .head.data); q.push(rightChild); this .head = this .head.next; } // 2.b) assign the left and right children of // parent parent.left = leftChild; parent.right = rightChild; } return node; } // Utility function to traverse the binary tree // after conversion inorderTraversal(node) { if (node != null ) { this .inorderTraversal(node.left); document.write(node.data + " " ); this .inorderTraversal(node.right); } } } // Driver code var tree = new BinaryTree(); /* Last node of Linked List */ tree.push(36); tree.push(30); tree.push(25); tree.push(15); tree.push(12); /* First node of Linked List */ tree.push(10); var node = tree.convertList2Binary(tree.root); document.write( "Inorder Traversal of the" + " constructed Binary Tree is:<br>" ); tree.inorderTraversal(node); </script> |
输出
Inorder Traversal of the constructed Binary Tree is: 25 12 30 10 36 15
时间复杂性: 上述解决方案的时间复杂度为O(n),其中n是节点数。
本文由 拉维·钱德拉·埃纳甘蒂 。如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请发表评论。
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



