让我们考虑下面的遍历: 顺序:D B E A F C 前序序列:A B D E C F
在预排序序列中,最左边的元素是树的根。所以我们知道A是给定序列的根。通过按顺序搜索“A”,我们可以发现“A”左边的所有元素都在左子树中,右边的元素在右子树中。现在我们知道了下面的结构。
A / / D B E F C
我们递归地遵循上面的步骤,得到下面的树。
A / / B C / / / /D E F
算法:buildTree() 1) 从预订单中选择一个元素。增加一个预排序索引变量(下面代码中的preIndex)以在下一个递归调用中选择下一个元素。 2) 创建一个新的树节点tNode,将数据作为拾取的元素。 3) 按顺序查找所选元素的索引。让索引为inIndex。 4) 在inIndex之前为元素调用buildTree,并将生成的树作为tNode的左子树。 5) 为inIndex之后的元素调用buildTree,并将生成的树作为tNode的正确子树。 6) 返回tNode。
C++
/* C++ program to construct tree using inorder and preorder traversals */ #include <bits/stdc++.h> using namespace std; /* A binary tree node has data, pointer to left child and a pointer to right child */ class node { public : char data; node* left; node* right; }; /* Prototypes for utility functions */ int search( char arr[], int strt, int end, char value); node* newNode( char data); /* Recursive function to construct binary of size len from Inorder traversal in[] and Preorder traversal pre[]. Initial values of inStrt and inEnd should be 0 and len -1. The function doesn't do any error checking for cases where inorder and preorder do not form a tree */ node* buildTree( char in[], char pre[], int inStrt, int inEnd) { static int preIndex = 0; if (inStrt > inEnd) return NULL; /* Pick current node from Preorder traversal using preIndex and increment preIndex */ node* tNode = newNode(pre[preIndex++]); /* If this node has no children then return */ if (inStrt == inEnd) return tNode; /* Else find the index of this node in Inorder traversal */ int inIndex = search(in, inStrt, inEnd, tNode->data); /* Using index in Inorder traversal, construct left and right subtress */ tNode->left = buildTree(in, pre, inStrt, inIndex - 1); tNode->right = buildTree(in, pre, inIndex + 1, inEnd); return tNode; } /* UTILITY FUNCTIONS */ /* Function to find index of value in arr[start...end] The function assumes that value is present in in[] */ int search( char arr[], int strt, int end, char value) { int i; for (i = strt; i <= end; i++) { if (arr[i] == value) return i; } } /* Helper function that allocates a new node with the given data and NULL left and right pointers. */ node* newNode( char data) { node* Node = new node(); Node->data = data; Node->left = NULL; Node->right = NULL; return (Node); } /* This function is here just to test buildTree() */ void printInorder(node* node) { if (node == NULL) return ; /* first recur on left child */ printInorder(node->left); /* then print the data of node */ cout<<node->data<< " " ; /* now recur on right child */ printInorder(node->right); } /* Driver code */ int main() { char in[] = { 'D' , 'B' , 'E' , 'A' , 'F' , 'C' }; char pre[] = { 'A' , 'B' , 'D' , 'E' , 'C' , 'F' }; int len = sizeof (in) / sizeof (in[0]); node* root = buildTree(in, pre, 0, len - 1); /* Let us test the built tree by printing Inorder traversal */ cout << "Inorder traversal of the constructed tree is " ; printInorder(root); } // This is code is contributed by rathbhupendra |
C
/* program to construct tree using inorder and preorder traversals */ #include <stdio.h> #include <stdlib.h> /* A binary tree node has data, pointer to left child and a pointer to right child */ struct node { char data; struct node* left; struct node* right; }; /* Prototypes for utility functions */ int search( char arr[], int strt, int end, char value); struct node* newNode( char data); /* Recursive function to construct binary of size len from Inorder traversal in[] and Preorder traversal pre[]. Initial values of inStrt and inEnd should be 0 and len -1. The function doesn't do any error checking for cases where inorder and preorder do not form a tree */ struct node* buildTree( char in[], char pre[], int inStrt, int inEnd) { static int preIndex = 0; if (inStrt > inEnd) return NULL; /* Pick current node from Preorder traversal using preIndex and increment preIndex */ struct node* tNode = newNode(pre[preIndex++]); /* If this node has no children then return */ if (inStrt == inEnd) return tNode; /* Else find the index of this node in Inorder traversal */ int inIndex = search(in, inStrt, inEnd, tNode->data); /* Using index in Inorder traversal, construct left and right subtress */ tNode->left = buildTree(in, pre, inStrt, inIndex - 1); tNode->right = buildTree(in, pre, inIndex + 1, inEnd); return tNode; } /* UTILITY FUNCTIONS */ /* Function to find index of value in arr[start...end] The function assumes that value is present in in[] */ int search( char arr[], int strt, int end, char value) { int i; for (i = strt; i <= end; i++) { if (arr[i] == value) return i; } } /* Helper function that allocates a new node with the given data and NULL left and right pointers. */ struct node* newNode( char data) { struct node* node = ( struct node*) malloc ( sizeof ( struct node)); node->data = data; node->left = NULL; node->right = NULL; return (node); } /* This function is here just to test buildTree() */ void printInorder( struct node* node) { if (node == NULL) return ; /* first recur on left child */ printInorder(node->left); /* then print the data of node */ printf ( "%c " , node->data); /* now recur on right child */ printInorder(node->right); } /* Driver program to test above functions */ int main() { char in[] = { 'D' , 'B' , 'E' , 'A' , 'F' , 'C' }; char pre[] = { 'A' , 'B' , 'D' , 'E' , 'C' , 'F' }; int len = sizeof (in) / sizeof (in[0]); struct node* root = buildTree(in, pre, 0, len - 1); /* Let us test the built tree by printing Inorder traversal */ printf ( "Inorder traversal of the constructed tree is " ); printInorder(root); getchar (); } |
JAVA
// Java program to construct a tree using inorder and preorder traversal /* A binary tree node has data, pointer to left child and a pointer to right child */ class Node { char data; Node left, right; Node( char item) { data = item; left = right = null ; } } class BinaryTree { Node root; static int preIndex = 0 ; /* Recursive function to construct binary of size len from Inorder traversal in[] and Preorder traversal pre[]. Initial values of inStrt and inEnd should be 0 and len -1. The function doesn't do any error checking for cases where inorder and preorder do not form a tree */ Node buildTree( char in[], char pre[], int inStrt, int inEnd) { if (inStrt > inEnd) return null ; /* Pick current node from Preorder traversal using preIndex and increment preIndex */ Node tNode = new Node(pre[preIndex++]); /* If this node has no children then return */ if (inStrt == inEnd) return tNode; /* Else find the index of this node in Inorder traversal */ int inIndex = search(in, inStrt, inEnd, tNode.data); /* Using index in Inorder traversal, construct left and right subtress */ tNode.left = buildTree(in, pre, inStrt, inIndex - 1 ); tNode.right = buildTree(in, pre, inIndex + 1 , inEnd); return tNode; } /* UTILITY FUNCTIONS */ /* Function to find index of value in arr[start...end] The function assumes that value is present in in[] */ int search( char arr[], int strt, int end, char value) { int i; for (i = strt; i <= end; i++) { if (arr[i] == value) return i; } return i; } /* This function is here just to test buildTree() */ void printInorder(Node node) { if (node == null ) return ; /* first recur on left child */ printInorder(node.left); /* then print the data of node */ System.out.print(node.data + " " ); /* now recur on right child */ printInorder(node.right); } // driver program to test above functions public static void main(String args[]) { BinaryTree tree = new BinaryTree(); char in[] = new char [] { 'D' , 'B' , 'E' , 'A' , 'F' , 'C' }; char pre[] = new char [] { 'A' , 'B' , 'D' , 'E' , 'C' , 'F' }; int len = in.length; Node root = tree.buildTree(in, pre, 0 , len - 1 ); // building the tree by printing inorder traversal System.out.println( "Inorder traversal of constructed tree is : " ); tree.printInorder(root); } } // This code has been contributed by Mayank Jaiswal |
蟒蛇3
# Python program to construct tree using inorder and # preorder traversals # A binary tree node class Node: # Constructor to create a new node def __init__( self , data): self .data = data self .left = None self .right = None """Recursive function to construct binary of size len from Inorder traversal in[] and Preorder traversal pre[]. Initial values of inStrt and inEnd should be 0 and len -1. The function doesn't do any error checking for cases where inorder and preorder do not form a tree """ def buildTree(inOrder, preOrder, inStrt, inEnd): if (inStrt > inEnd): return None # Pick current node from Preorder traversal using # preIndex and increment preIndex tNode = Node(preOrder[buildTree.preIndex]) buildTree.preIndex + = 1 # If this node has no children then return if inStrt = = inEnd : return tNode # Else find the index of this node in Inorder traversal inIndex = search(inOrder, inStrt, inEnd, tNode.data) # Using index in Inorder Traversal, construct left # and right subtrees tNode.left = buildTree(inOrder, preOrder, inStrt, inIndex - 1 ) tNode.right = buildTree(inOrder, preOrder, inIndex + 1 , inEnd) return tNode # UTILITY FUNCTIONS # Function to find index of value in arr[start...end] # The function assumes that value is present in inOrder[] def search(arr, start, end, value): for i in range (start, end + 1 ): if arr[i] = = value: return i def printInorder(node): if node is None : return # first recur on left child printInorder(node.left) # then print the data of node print (node.data,end = ' ' ) # now recur on right child printInorder(node.right) # Driver program to test above function inOrder = [ 'D' , 'B' , 'E' , 'A' , 'F' , 'C' ] preOrder = [ 'A' , 'B' , 'D' , 'E' , 'C' , 'F' ] # Static variable preIndex buildTree.preIndex = 0 root = buildTree(inOrder, preOrder, 0 , len (inOrder) - 1 ) # Let us test the build tree by printing Inorder traversal print ( "Inorder traversal of the constructed tree is" ) printInorder(root) # This code is contributed by Nikhil Kumar Singh(nickzuck_007) |
C#
// C# program to construct a tree using // inorder and preorder traversal using System; /* A binary tree node has data, pointer to left child and a pointer to right child */ public class Node { public char data; public Node left, right; public Node( char item) { data = item; left = right = null ; } } class GFG { public Node root; public static int preIndex = 0; /* Recursive function to construct binary of size len from Inorder traversal in[] and Preorder traversal pre[]. Initial values of inStrt and inEnd should be 0 and len -1. The function doesn't do any error checking for cases where inorder and preorder do not form a tree */ public virtual Node buildTree( char [] arr, char [] pre, int inStrt, int inEnd) { if (inStrt > inEnd) { return null ; } /* Pick current node from Preorder traversal using preIndex and increment preIndex */ Node tNode = new Node(pre[preIndex++]); /* If this node has no children then return */ if (inStrt == inEnd) { return tNode; } /* Else find the index of this node in Inorder traversal */ int inIndex = search(arr, inStrt, inEnd, tNode.data); /* Using index in Inorder traversal, construct left and right subtress */ tNode.left = buildTree(arr, pre, inStrt, inIndex - 1); tNode.right = buildTree(arr, pre, inIndex + 1, inEnd); return tNode; } /* UTILITY FUNCTIONS */ /* Function to find index of value in arr[start...end] The function assumes that value is present in in[] */ public virtual int search( char [] arr, int strt, int end, char value) { int i; for (i = strt; i <= end; i++) { if (arr[i] == value) { return i; } } return i; } /* This function is here just to test buildTree() */ public virtual void printInorder(Node node) { if (node == null ) { return ; } /* first recur on left child */ printInorder(node.left); /* then print the data of node */ Console.Write(node.data + " " ); /* now recur on right child */ printInorder(node.right); } // Driver Code public static void Main( string [] args) { GFG tree = new GFG(); char [] arr = new char [] { 'D' , 'B' , 'E' , 'A' , 'F' , 'C' }; char [] pre = new char [] { 'A' , 'B' , 'D' , 'E' , 'C' , 'F' }; int len = arr.Length; Node root = tree.buildTree(arr, pre, 0, len - 1); // building the tree by printing inorder traversal Console.WriteLine( "Inorder traversal of " + "constructed tree is : " ); tree.printInorder(root); } } // This code is contributed by Shrikant13 |
Javascript
<script> // Javascript program to construct a // tree using inorder and preorder traversal // A binary tree node has data, pointer // to left child and a pointer to right child class Node { constructor(item) { this .data = item; this .left = this .right = null ; } } let root; let preIndex = 0; // Recursive function to construct binary // of size len from Inorder traversal in[] // and Preorder traversal pre[]. Initial // values of inStrt and inEnd should be 0 // and len -1. The function doesn't do any // error checking for cases where inorder // and preorder do not form a tree function buildTree(In, pre, inStrt, inEnd) { if (inStrt > inEnd) return null ; // Pick current node from Preorder // traversal using preIndex and // increment preIndex let tNode = new Node(pre[preIndex++]); // If this node has no children then return if (inStrt == inEnd) return tNode; // Else find the index of this // node in Inorder traversal let inIndex = search(In, inStrt, inEnd, tNode.data); // Using index in Inorder traversal, // construct left and right subtress tNode.left = buildTree(In, pre, inStrt, inIndex - 1); tNode.right = buildTree(In, pre, inIndex + 1, inEnd); return tNode; } /* UTILITY FUNCTIONS */ // Function to find index of value // in arr[start...end]. The function // assumes that value is present in in[] function search(arr, strt, end, value) { let i; for (i = strt; i <= end; i++) { if (arr[i] == value) return i; } return i; } // This function is here just // to test buildTree() function printInorder(node) { if (node == null ) return ; // First recur on left child printInorder(node.left); // Then print the data of node document.write(node.data + " " ); // Now recur on right child printInorder(node.right); } // Driver code let In = [ 'D ', ' B ', ' E ', ' A ', ' F ', ' C ' ]; let pre = [ ' A ', ' B ', ' D ', ' E ', ' C ', ' F']; let len = In.length; root = buildTree(In, pre, 0, len - 1); // Building the tree by printing // inorder traversal document.write( "Inorder traversal of " + "constructed tree is : <br>" ); printInorder(root); // This code is contributed by patel2127 </script> |
Inorder traversal of the constructed tree is D B E A F C
时间复杂度:O(n^2) .最坏的情况发生在树倾斜的时候。最坏情况下的前序和顺序遍历示例为{A,B,C,D}和{D,C,B,A}。
有效方法: 我们可以使用哈希(C++中的无序排序映射或java中的HashMap)来优化上述解决方案。我们将按序遍历的索引存储在哈希表中。这样搜索就可以一次性完成。
C++
/* C++ program to construct tree using inorder and preorder traversals */ #include <bits/stdc++.h> using namespace std; /* A binary tree node has data, pointer to left child and a pointer to right child */ struct Node { char data; struct Node* left; struct Node* right; }; struct Node* newNode( char data) { struct Node* node = new Node; node->data = data; node->left = node->right = NULL; return (node); } /* Recursive function to construct binary of size len from Inorder traversal in[] and Preorder traversal pre[]. Initial values of inStrt and inEnd should be 0 and len -1. The function doesn't do any error checking for cases where inorder and preorder do not form a tree */ struct Node* buildTree( char in[], char pre[], int inStrt, int inEnd, unordered_map< char , int >& mp) { static int preIndex = 0; if (inStrt > inEnd) return NULL; /* Pick current node from Preorder traversal using preIndex and increment preIndex */ char curr = pre[preIndex++]; struct Node* tNode = newNode(curr); /* If this node has no children then return */ if (inStrt == inEnd) return tNode; /* Else find the index of this node in Inorder traversal */ int inIndex = mp[curr]; /* Using index in Inorder traversal, construct left and right subtress */ tNode->left = buildTree(in, pre, inStrt, inIndex - 1, mp); tNode->right = buildTree(in, pre, inIndex + 1, inEnd, mp); return tNode; } // This function mainly creates an unordered_map, then // calls buildTree() struct Node* buldTreeWrap( char in[], char pre[], int len) { // Store indexes of all items so that we // we can quickly find later unordered_map< char , int > mp; for ( int i = 0; i < len; i++) mp[in[i]] = i; return buildTree(in, pre, 0, len - 1, mp); } /* This function is here just to test buildTree() */ void printInorder( struct Node* node) { if (node == NULL) return ; printInorder(node->left); printf ( "%c " , node->data); printInorder(node->right); } /* Driver program to test above functions */ int main() { char in[] = { 'D' , 'B' , 'E' , 'A' , 'F' , 'C' }; char pre[] = { 'A' , 'B' , 'D' , 'E' , 'C' , 'F' }; int len = sizeof (in) / sizeof (in[0]); struct Node* root = buldTreeWrap(in, pre, len); /* Let us test the built tree by printing Inorder traversal */ printf ( "Inorder traversal of the constructed tree is " ); printInorder(root); } |
JAVA
/* Java program to construct tree using inorder and preorder traversals */ import java.io.*; import java.util.*; /* A binary tree node has data, pointer to left child and a pointer to right child */ class Node { char data; Node left,right; Node( char item) { data = item; left = right = null ; } } class Tree { public static Node root; // Store indexes of all items so that we // we can quickly find later static HashMap<Character,Integer> mp = new HashMap<>(); static int preIndex = 0 ; /* Recursive function to construct binary of size len from Inorder traversal in[] and Preorder traversal pre[]. Initial values of inStrt and inEnd should be 0 and len -1. The function doesn't do any error checking for cases where inorder and preorder do not form a tree */ public static Node buildTree( char [] in, char [] pre, int inStrt, int inEnd) { if (inStrt > inEnd) { return null ; } /* Pick current node from Preorder traversal using preIndex and increment preIndex */ char curr = pre[preIndex++]; Node tNode; tNode = new Node(curr); /* If this node has no children then return */ if (inStrt == inEnd) { return tNode; } /* Else find the index of this node in Inorder traversal */ int inIndex = mp.get(curr); /* Using index in Inorder traversal, construct left and right subtress */ tNode.left = buildTree(in, pre, inStrt, inIndex - 1 ); tNode.right = buildTree(in, pre, inIndex + 1 , inEnd); return tNode; } // This function mainly creates an unordered_map, then // calls buildTree() public static Node buldTreeWrap( char [] in, char [] pre, int len) { for ( int i = 0 ; i < len; i++) { mp.put(in[i], i); } return buildTree(in, pre, 0 , len - 1 ); } /* This function is here just to test buildTree() */ static void printInorder(Node node) { if (node == null ) { return ; } printInorder(node.left); System.out.print(node.data + " " ); printInorder(node.right); } /* Driver code */ public static void main (String[] args) { char [] in = { 'D' , 'B' , 'E' , 'A' , 'F' , 'C' }; char [] pre = { 'A' , 'B' , 'D' , 'E' , 'C' , 'F' }; int len = in.length; Tree.root=buldTreeWrap(in, pre, len); /* Let us test the built tree by printing Inorder traversal */ System.out.println( "Inorder traversal of the constructed tree is" ); printInorder(root); } } // This code is contributed by avanitrachhadiya2155 |
蟒蛇3
# Python3 program to construct tree using inorder # and preorder traversals # A binary tree node has data, pointer to left child # and a pointer to right child class Node: def __init__( self , x): self .data = x self .left = None self .right = None # Recursive function to construct binary of size # len from Inorder traversal in[] and Preorder traversal # pre[]. Initial values of inStrt and inEnd should be # 0 and len -1. The function doesn't do any error # checking for cases where inorder and preorder # do not form a tree def buildTree(inn, pre, inStrt, inEnd): global preIndex, mp if (inStrt > inEnd): return None # Pick current node from Preorder traversal # using preIndex and increment preIndex curr = pre[preIndex] preIndex + = 1 tNode = Node(curr) # If this node has no children then return if (inStrt = = inEnd): return tNode # Else find the index of this # node in Inorder traversal inIndex = mp[curr] # Using index in Inorder traversal, # construct left and right subtress tNode.left = buildTree(inn, pre, inStrt, inIndex - 1 ) tNode.right = buildTree(inn, pre, inIndex + 1 , inEnd) return tNode # This function mainly creates an # unordered_map, then calls buildTree() def buldTreeWrap(inn, pre, lenn): global mp # Store indexes of all items so that we # we can quickly find later # unordered_map<char, int> mp; for i in range (lenn): mp[inn[i]] = i return buildTree(inn, pre, 0 , lenn - 1 ) # This function is here just to test buildTree() def prInorder(node): if (node = = None ): return prInorder(node.left) print (node.data, end = " " ) prInorder(node.right) # Driver code if __name__ = = '__main__' : mp = {} preIndex = 0 inn = [ 'D' , 'B' , 'E' , 'A' , 'F' , 'C' ] pre = [ 'A' , 'B' , 'D' , 'E' , 'C' , 'F' ] lenn = len (inn) root = buldTreeWrap(inn, pre,lenn) # Let us test the built tree by printing # Inorder traversal print ( "Inorder traversal of " "the constructed tree is" ) prInorder(root) # This code is contributed by mohit kumar 29 |
C#
/* C# program to construct tree using inorder and preorder traversals */ using System; using System.Collections.Generic; /* A binary tree node has data, pointer to left child and a pointer to right child */ public class Node { public char data; public Node left, right; public Node( char d) { data = d; left = right = null ; } } public class Tree { public static Node root; // Store indexes of all items so that we // we can quickly find later static Dictionary< char , int > mp = new Dictionary< char , int >(); static int preIndex = 0; /* Recursive function to construct binary of size len from Inorder traversal in[] and Preorder traversal pre[]. Initial values of inStrt and inEnd should be 0 and len -1. The function doesn't do any error checking for cases where inorder and preorder do not form a tree */ static Node buildTree( char [] In, char [] pre, int inStrt, int inEnd) { if (inStrt > inEnd) { return null ; } /* Pick current node from Preorder traversal using preIndex and increment preIndex */ char curr = pre[preIndex++]; Node tNode; tNode = new Node(curr); /* If this node has no children then return */ if (inStrt == inEnd) { return tNode; } /* Else find the index of this node in Inorder traversal */ int inIndex = mp[curr]; /* Using index in Inorder traversal, construct left and right subtress */ tNode.left = buildTree(In, pre, inStrt, inIndex - 1); tNode.right = buildTree(In, pre, inIndex + 1, inEnd); return tNode; } // This function mainly creates an unordered_map, then // calls buildTree() public static Node buldTreeWrap( char [] In, char [] pre, int len) { for ( int i = 0; i < len; i++) { mp.Add(In[i], i); } return buildTree(In, pre, 0, len - 1); } /* This function is here just to test buildTree() */ static void printInorder(Node node) { if (node == null ) { return ; } printInorder(node.left); Console.Write(node.data + " " ); printInorder(node.right); } /* Driver code */ static public void Main (){ char [] In = { 'D' , 'B' , 'E' , 'A' , 'F' , 'C' }; char [] pre = { 'A' , 'B' , 'D' , 'E' , 'C' , 'F' }; int len = In.Length; Tree.root = buldTreeWrap(In, pre, len); /* Let us test the built tree by printing Inorder traversal */ Console.WriteLine( "Inorder traversal of the constructed tree is" ); printInorder(Tree.root); } } // This code is contributed by rag2127 |
Inorder traversal of the constructed tree is D B E A F C
时间复杂性: O(n) 另一种方法: 使用这样一个事实:按序遍历是左向右根,按序遍历是左向右根。此外,前序遍历中的第一个节点始终是根节点,而按序遍历中的第一个节点是树中最左边的节点。 维护两个数据结构:Stack(用于存储我们在遍历PreOrder数组时访问的路径)和Set(用于维护下一个右子树所在的节点)。
1.执行以下操作,直到到达最左边的节点。 继续从前序遍历创建节点 如果堆栈最顶端的元素不在集合中,请将创建的节点链接到堆栈最顶端元素(如果有)的左子元素,而不弹出该元素。 否则,将创建的节点链接到堆栈最顶层元素的右子级。从集合和堆栈中移除堆栈最顶部的元素。 将节点推到堆栈中。

2.不断从堆栈中弹出节点,直到堆栈为空,或者堆栈的最顶层元素与顺序遍历的当前元素进行比较。循环结束后,将最后一个节点推回到堆栈和集合中。
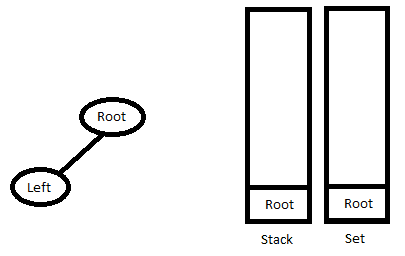
3.转到第一步。
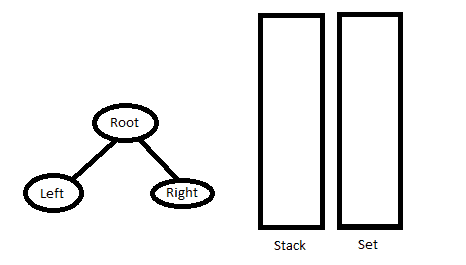
C++
// C++ program to construct a tree using // inorder and preorder traversal #include<bits/stdc++.h> using namespace std; class TreeNode { public : int val; TreeNode* left; TreeNode* right; TreeNode( int x) { val = x; } }; set<TreeNode*> s; stack<TreeNode*> st; // Function to build tree using given traversal TreeNode* buildTree( int preorder[], int inorder[], int n) { TreeNode* root = NULL; for ( int pre = 0, in = 0; pre < n;) { TreeNode* node = NULL; do { node = new TreeNode(preorder[pre]); if (root == NULL) { root = node; } if (st.size() > 0) { if (s.find(st.top()) != s.end()) { s.erase(st.top()); st.top()->right = node; st.pop(); } else { st.top()->left = node; } } st.push(node); } while (preorder[pre++] != inorder[in] && pre < n); node = NULL; while (st.size() > 0 && in < n && st.top()->val == inorder[in]) { node = st.top(); st.pop(); in++; } if (node != NULL) { s.insert(node); st.push(node); } } return root; } // Function to print tree in Inorder void printInorder(TreeNode* node) { if (node == NULL) return ; /* first recur on left child */ printInorder(node->left); /* then print the data of node */ cout << node->val << " " ; /* now recur on right child */ printInorder(node->right); } // Driver code int main() { int in[] = { 9, 8, 4, 2, 10, 5, 10, 1, 6, 3, 13, 12, 7 }; int pre[] = { 1, 2, 4, 8, 9, 5, 10, 10, 3, 6, 7, 12, 13 }; int len = sizeof (in)/ sizeof ( int ); TreeNode *root = buildTree(pre, in, len); printInorder(root); return 0; } // This code is contributed by Arnab Kundu |
JAVA
// Java program to construct a tree using inorder and preorder traversal import java.util.*; public class TreeNode { int val; TreeNode left; TreeNode right; TreeNode( int x) { val = x; } } class BinaryTree { static Set<TreeNode> set = new HashSet<>(); static Stack<TreeNode> stack = new Stack<>(); // Function to build tree using given traversal public TreeNode buildTree( int [] preorder, int [] inorder) { TreeNode root = null ; for ( int pre = 0 , in = 0 ; pre < preorder.length;) { TreeNode node = null ; do { node = new TreeNode(preorder[pre]); if (root == null ) { root = node; } if (!stack.isEmpty()) { if (set.contains(stack.peek())) { set.remove(stack.peek()); stack.pop().right = node; } else { stack.peek().left = node; } } stack.push(node); } while (preorder[pre++] != inorder[in] && pre < preorder.length); node = null ; while (!stack.isEmpty() && in < inorder.length && stack.peek().val == inorder[in]) { node = stack.pop(); in++; } if (node != null ) { set.add(node); stack.push(node); } } return root; } // Function to print tree in Inorder void printInorder(TreeNode node) { if (node == null ) return ; /* first recur on left child */ printInorder(node.left); /* then print the data of node */ System.out.print(node.val + " " ); /* now recur on right child */ printInorder(node.right); } // driver program to test above functions public static void main(String args[]) { BinaryTree tree = new BinaryTree(); int in[] = new int [] { 9 , 8 , 4 , 2 , 10 , 5 , 10 , 1 , 6 , 3 , 13 , 12 , 7 }; int pre[] = new int [] { 1 , 2 , 4 , 8 , 9 , 5 , 10 , 10 , 3 , 6 , 7 , 12 , 13 }; int len = in.length; TreeNode root = tree.buildTree(pre, in); tree.printInorder(root); } } |
蟒蛇3
# Python3 program to construct a tree using # inorder and preorder traversal class TreeNode: def __init__( self , x): self .val = x self .left = None self .right = None s = set () st = [] # Function to build tree using given traversal def buildTree(preorder, inorder, n): root = None ; pre = 0 in_t = 0 while pre < n: node = None ; while True : node = TreeNode(preorder[pre]) if (root = = None ): root = node; if ( len (st) > 0 ): if (st[ - 1 ] in s): s.discard(st[ - 1 ]); st[ - 1 ].right = node; st.pop(); else : st[ - 1 ].left = node; st.append(node); if pre> = n or preorder[pre] = = inorder[in_t]: pre + = 1 break pre + = 1 node = None ; while ( len (st) > 0 and in_t < n and st[ - 1 ].val = = inorder[in_t]): node = st[ - 1 ]; st.pop(); in_t + = 1 if (node ! = None ): s.add(node); st.append(node); return root; # Function to print tree in_t Inorder def printInorder( node): if (node = = None ): return ; ''' first recur on left child ''' printInorder(node.left); ''' then print data of node ''' print (node.val, end = " " ); ''' now recur on right child ''' printInorder(node.right); # Driver code if __name__ = = '__main__' : in_t = [ 9 , 8 , 4 , 2 , 10 , 5 , 10 , 1 , 6 , 3 , 13 , 12 , 7 ] pre = [ 1 , 2 , 4 , 8 , 9 , 5 , 10 , 10 , 3 , 6 , 7 , 12 , 13 ] l = len (in_t) root = buildTree(pre, in_t, l); printInorder(root); # This code is contributed by rutvik_56. |
C#
// C# program to construct a tree // using inorder and preorder traversal using System; using System.Collections.Generic; public class TreeNode { public int val; public TreeNode left; public TreeNode right; public TreeNode( int x) { val = x; } } class GFG { static HashSet<TreeNode> set = new HashSet<TreeNode>(); static Stack<TreeNode> stack = new Stack<TreeNode>(); // Function to build tree using given traversal public TreeNode buildTree( int [] preorder, int [] inorder) { TreeNode root = null ; for ( int pre = 0, iN = 0; pre < preorder.Length;) { TreeNode node = null ; do { node = new TreeNode(preorder[pre]); if (root == null ) { root = node; } if (stack.Count != 0) { if ( set .Contains(stack.Peek())) { set .Remove(stack.Peek()); stack.Pop().right = node; } else { stack.Peek().left = node; } } stack.Push(node); } while (preorder[pre++] != inorder[iN] && pre < preorder.Length); node = null ; while (stack.Count != 0 && iN < inorder.Length && stack.Peek().val == inorder[iN]) { node = stack.Pop(); iN++; } if (node != null ) { set .Add(node); stack.Push(node); } } return root; } // Function to print tree in Inorder void printInorder(TreeNode node) { if (node == null ) return ; /* first recur on left child */ printInorder(node.left); /* then print the data of node */ Console.Write(node.val + " " ); /* now recur on right child */ printInorder(node.right); } // Driver Code public static void Main(String []args) { GFG tree = new GFG(); int []iN = new int [] { 9, 8, 4, 2, 10, 5, 10, 1, 6, 3, 13, 12, 7 }; int []pre = new int [] { 1, 2, 4, 8, 9, 5, 10, 10, 3, 6, 7, 12, 13 }; int len = iN.Length; TreeNode root = tree.buildTree(pre, iN); tree.printInorder(root); } } // This code is contributed by 29AjayKumar |
Javascript
<script> // Javascript program to construct a tree using inorder and preorder traversal class TreeNode { constructor(x) { this .val = x; this .left = null ; this .right = null ; } } let set = new Set(); let stack = []; // Function to build tree using given traversal function buildTree(preorder,inorder) { let root = null ; for (let pre = 0,In=0; pre < preorder.length;) { let node = null ; do { node = new TreeNode(preorder[pre]); if (root == null ) { root = node; } if (stack.length!=0) { if (set.has(stack[stack.length-1])) { set. delete (stack[stack.length-1]); stack.pop().right = node; } else { stack[stack.length-1].left = node; } } stack.push(node); } while (preorder[pre++] != inorder[In] && pre < preorder.length); node = null ; while (stack.length!=0 && In < inorder.length && stack[stack.length-1].val == inorder[In]) { node = stack.pop(); In++; } if (node != null ) { set.add(node); stack.push(node); } } return root; } // Function to print tree in Inorder function printInorder(node) { if (node == null ) return ; /* first recur on left child */ printInorder(node.left); /* then print the data of node */ document.write(node.val + " " ); /* now recur on right child */ printInorder(node.right); } // driver program to test above functions let In=[9, 8, 4, 2, 10, 5, 10, 1, 6, 3, 13, 12, 7 ]; let pre=[1, 2, 4, 8, 9, 5, 10, 10, 3, 6, 7, 12, 13 ]; let len = In.length; let root=buildTree(pre, In); printInorder(root); // This code is contributed by unknown2108 </script> |
9 8 4 2 10 5 10 1 6 3 13 12 7


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



