使用堆栈检查表达式中的平衡括号（格式良好）-yiteyi-C++库

给定一个表达式字符串exp，编写一个程序来检查exp中的对和“{”、“}”、“（“，”）、“[”、“]”的顺序是否正确。

null

实例 :

输入：exp=“[（）]{}{[（）（）]（）}” 输出：平衡的

输入：exp=“[（]）” 输出：不平衡

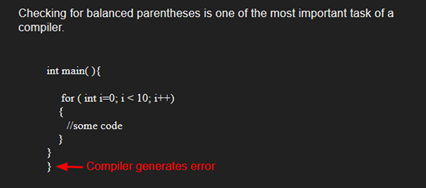
check-for-balanced-parentheses-in-an-expression

建议：请在“上解决” 实践 “首先，在讨论解决方案之前。

算法：

声明一个字符堆栈 s
现在遍历表达式字符串exp。
1. 如果当前字符是起始括号( “（”或“{”或“[” )然后把它推到堆栈上。
2. 如果当前字符是右括号( “）”或“}”或“]” )然后从堆栈中弹出，如果弹出的字符是匹配的起始括号，则fine else括号不平衡。
完成遍历后，如果堆栈中还剩下一些起始括号，则“不平衡”

下图是上述方法的试运行：

图片[2]-使用堆栈检查表达式中的平衡括号（格式良好）-yiteyi-C++库

以下是上述方法的实施情况：

C++

                         // CPP program to check for balanced brackets.                       
                         #include <bits/stdc++.h>                       
                         using                                     namespace                                     std;                       
           
                         // function to check if brackets are balanced                       
                         bool                                     areBracketsBalanced(string expr)                       
                         {                       
                                                 stack<                                     char                                     > s;                       
                                                 char                                     x;                       
           
                                                 // Traversing the Expression                       
                                                 for                                     (                                     int                                     i = 0; i < expr.length(); i++)                       
                                                 {                       
                                                 if                                     (expr[i] ==                                     '('                                     || expr[i] ==                                     '['                       
                                                 || expr[i] ==                                     '{'                                     )                       
                                                 {                       
                                                 // Push the element in the stack                       
                                                 s.push(expr[i]);                       
                                                 continue                                     ;                       
                                                 }                       
           
                                                 // IF current current character is not opening                       
                                                 // bracket, then it must be closing. So stack                       
                                                 // cannot be empty at this point.                       
                                                 if                                     (s.empty())                       
                                                 return                                     false                                     ;                       
           
                                                 switch                                     (expr[i]) {                       
                                                 case                                     ')'                                     :                       
                                   
                                                 // Store the top element in a                       
                                                 x = s.top();                       
                                                 s.pop();                       
                                                 if                                     (x ==                                     '{'                                     || x ==                                     '['                                     )                       
                                                 return                                     false                                     ;                       
                                                 break                                     ;                       
           
                                                 case                                     '}'                                     :                       
           
                                                 // Store the top element in b                       
                                                 x = s.top();                       
                                                 s.pop();                       
                                                 if                                     (x ==                                     '('                                     || x ==                                     '['                                     )                       
                                                 return                                     false                                     ;                       
                                                 break                                     ;                       
           
                                                 case                                     ']'                                     :                       
           
                                                 // Store the top element in c                       
                                                 x = s.top();                       
                                                 s.pop();                       
                                                 if                                     (x ==                                     '('                                     || x ==                                     '{'                                     )                       
                                                 return                                     false                                     ;                       
                                                 break                                     ;                       
                                                 }                       
                                                 }                       
           
                                                 // Check Empty Stack                       
                                                 return                                     (s.empty());                       
                         }                       
           
                         // Driver code                       
                         int                                     main()                       
                         {                       
                                                 string expr =                                     "{()}[]"                                     ;                       
           
                                                 // Function call                       
                                                 if                                     (areBracketsBalanced(expr))                       
                                                 cout <<                                     "Balanced"                                     ;                       
                                                 else                       
                                                 cout <<                                     "Not Balanced"                                     ;                       
                                                 return                                     0;                       
                         }                       

C

                         #include <stdio.h>                       
                         #include <stdlib.h>                       
                         #define bool int                       
           
                         // structure of a stack node                       
                         struct                                     sNode {                       
                                                 char                                     data;                       
                                                 struct                                     sNode* next;                       
                         };                       
           
                         // Function to push an item to stack                       
                         void                                     push(                                     struct                                     sNode** top_ref,                                     int                                     new_data);                       
           
                         // Function to pop an item from stack                       
                         int                                     pop(                                     struct                                     sNode** top_ref);                       
           
                         // Returns 1 if character1 and character2 are matching left                       
                         // and right Brackets                       
                         bool                                     isMatchingPair(                                     char                                     character1,                                     char                                     character2)                       
                         {                       
                                                 if                                     (character1 ==                                     '('                                     && character2 ==                                     ')'                                     )                       
                                                 return                                     1;                       
                                                 else                                     if                                     (character1 ==                                     '{'                                     && character2 ==                                     '}'                                     )                       
                                                 return                                     1;                       
                                                 else                                     if                                     (character1 ==                                     '['                                     && character2 ==                                     ']'                                     )                       
                                                 return                                     1;                       
                                                 else                       
                                                 return                                     0;                       
                         }                       
           
                         // Return 1 if expression has balanced Brackets                       
                         bool                                     areBracketsBalanced(                                     char                                     exp                                     [])                       
                         {                       
                                                 int                                     i = 0;                       
           
                                                 // Declare an empty character stack                       
                                                 struct                                     sNode* stack = NULL;                       
           
                                                 // Traverse the given expression to check matching                       
                                                 // brackets                       
                                                 while                                     (                                     exp                                     [i])                       
                                                 {                       
                                                 // If the exp[i] is a starting bracket then push                       
                                                 // it                       
                                                 if                                     (                                     exp                                     [i] ==                                     '{'                                     ||                                     exp                                     [i] ==                                     '('                                     ||                                     exp                                     [i] ==                                     '['                                     )                       
                                                 push(&stack,                                     exp                                     [i]);                       
           
                                                 // If exp[i] is an ending bracket then pop from                       
                                                 // stack and check if the popped bracket is a                       
                                                 // matching pair*/                       
                                                 if                                     (                                     exp                                     [i] ==                                     '}'                                     ||                                     exp                                     [i] ==                                     ')'                       
                                                 ||                                     exp                                     [i] ==                                     ']'                                     ) {                       
           
                                                 // If we see an ending bracket without a pair                       
                                                 // then return false                       
                                                 if                                     (stack == NULL)                       
                                                 return                                     0;                       
           
                                                 // Pop the top element from stack, if it is not                       
                                                 // a pair bracket of character then there is a                       
                                                 // mismatch.                       
                                                 // his happens for expressions like {(})                       
                                                 else                                     if                                     (!isMatchingPair(pop(&stack),                                     exp                                     [i]))                       
                                                 return                                     0;                       
                                                 }                       
                                                 i++;                       
                                                 }                       
           
                                                 // If there is something left in expression then there                       
                                                 // is a starting bracket without a closing                       
                                                 // bracket                       
                                                 if                                     (stack == NULL)                       
                                                 return                                     1;                                     // balanced                       
                                                 else                       
                                                 return                                     0;                                     // not balanced                       
                         }                       
           
                         // Driver code                       
                         int                                     main()                       
                         {                       
                                                 char                                     exp                                     [100] =                                     "{()}[]"                                     ;                       
           
                                                 // Function call                       
                                                 if                                     (areBracketsBalanced(                                     exp                                     ))                       
                                                 printf                                     (                                     "Balanced "                                     );                       
                                                 else                       
                                                 printf                                     (                                     "Not Balanced "                                     );                       
                                                 return                                     0;                       
                         }                       
           
                         // Function to push an item to stack                       
                         void                                     push(                                     struct                                     sNode** top_ref,                                     int                                     new_data)                       
                         {                       
                                                 // allocate node                       
                                                 struct                                     sNode* new_node                       
                                                 = (                                     struct                                     sNode*)                                     malloc                                     (                                     sizeof                                     (                                     struct                                     sNode));                       
           
                                                 if                                     (new_node == NULL) {                       
                                                 printf                                     (                                     "Stack overflow n"                                     );                       
                                                 getchar                                     ();                       
                                                 exit                                     (0);                       
                                                 }                       
           
                                                 // put in the data                       
                                                 new_node->data = new_data;                       
           
                                                 // link the old list off the new node                       
                                                 new_node->next = (*top_ref);                       
           
                                                 // move the head to point to the new node                       
                                                 (*top_ref) = new_node;                       
                         }                       
           
                         // Function to pop an item from stack                       
                         int                                     pop(                                     struct                                     sNode** top_ref)                       
                         {                       
                                                 char                                     res;                       
                                                 struct                                     sNode* top;                       
           
                                                 // If stack is empty then error                       
                                                 if                                     (*top_ref == NULL) {                       
                                                 printf                                     (                                     "Stack overflow n"                                     );                       
                                                 getchar                                     ();                       
                                                 exit                                     (0);                       
                                                 }                       
                                                 else                                     {                       
                                                 top = *top_ref;                       
                                                 res = top->data;                       
                                                 *top_ref = top->next;                       
                                                 free                                     (top);                       
                                                 return                                     res;                       
                                                 }                       
                         }                       

JAVA

                         // Java program for checking                       
                         // balanced brackets                       
                         import                                     java.util.*;                       
           
                         public                                     class                                     BalancedBrackets {                       
           
                                                 // function to check if brackets are balanced                       
                                                 static                                     boolean                                     areBracketsBalanced(String expr)                       
                                                 {                       
                                                 // Using ArrayDeque is faster than using Stack class                       
                                                 Deque<Character> stack                       
                                                 =                                     new                                     ArrayDeque<Character>();                       
           
                                                 // Traversing the Expression                       
                                                 for                                     (                                     int                                     i =                                     0                                     ; i < expr.length(); i++)                       
                                                 {                       
                                                 char                                     x = expr.charAt(i);                       
           
                                                 if                                     (x ==                                     '('                                     || x ==                                     '['                                     || x ==                                     '{'                                     )                       
                                                 {                       
                                                 // Push the element in the stack                       
                                                 stack.push(x);                       
                                                 continue                                     ;                       
                                                 }                       
           
                                                 // If current character is not opening                       
                                                 // bracket, then it must be closing. So stack                       
                                                 // cannot be empty at this point.                       
                                                 if                                     (stack.isEmpty())                       
                                                 return                                     false                                     ;                       
                                                 char                                     check;                       
                                                 switch                                     (x) {                       
                                                 case                                     ')'                                     :                       
                                                 check = stack.pop();                       
                                                 if                                     (check ==                                     '{'                                     || check ==                                     '['                                     )                       
                                                 return                                     false                                     ;                       
                                                 break                                     ;                       
           
                                                 case                                     '}'                                     :                       
                                                 check = stack.pop();                       
                                                 if                                     (check ==                                     '('                                     || check ==                                     '['                                     )                       
                                                 return                                     false                                     ;                       
                                                 break                                     ;                       
           
                                                 case                                     ']'                                     :                       
                                                 check = stack.pop();                       
                                                 if                                     (check ==                                     '('                                     || check ==                                     '{'                                     )                       
                                                 return                                     false                                     ;                       
                                                 break                                     ;                       
                                                 }                       
                                                 }                       
           
                                                 // Check Empty Stack                       
                                                 return                                     (stack.isEmpty());                       
                                                 }                       
           
                                                 // Driver code                       
                                                 public                                     static                                     void                                     main(String[] args)                       
                                                 {                       
                                                 String expr =                                     "([{}])"                                     ;                       
           
                                                 // Function call                       
                                                 if                                     (areBracketsBalanced(expr))                       
                                                 System.out.println(                                     "Balanced "                                     );                       
                                                 else                       
                                                 System.out.println(                                     "Not Balanced "                                     );                       
                                                 }                       
                         }                       

蟒蛇3

                         # Python3 program to check for                       
                         # balanced brackets.                       
           
                         # function to check if                       
                         # brackets are balanced                       
           
           
                         def                                     areBracketsBalanced(expr):                       
                                                 stack                                     =                                     []                       
           
                                                 # Traversing the Expression                       
                                                 for                                     char                                     in                                     expr:                       
                                                 if                                     char                                     in                                     [                                     "("                                     ,                                     "{"                                     ,                                     "["                                     ]:                       
           
                                                 # Push the element in the stack                       
                                                 stack.append(char)                       
                                                 else                                     :                       
           
                                                 # IF current character is not opening                       
                                                 # bracket, then it must be closing.                       
                                                 # So stack cannot be empty at this point.                       
                                                 if                                     not                                     stack:                       
                                                 return                                     False                       
                                                 current_char                                     =                                     stack.pop()                       
                                                 if                                     current_char                                     =                                     =                                     '('                                     :                       
                                                 if                                     char !                                     =                                     ")"                                     :                       
                                                 return                                     False                       
                                                 if                                     current_char                                     =                                     =                                     '{'                                     :                       
                                                 if                                     char !                                     =                                     "}"                                     :                       
                                                 return                                     False                       
                                                 if                                     current_char                                     =                                     =                                     '['                                     :                       
                                                 if                                     char !                                     =                                     "]"                                     :                       
                                                 return                                     False                       
           
                                                 # Check Empty Stack                       
                                                 if                                     stack:                       
                                                 return                                     False                       
                                                 return                                     True                       
           
           
                         # Driver Code                       
                         if                                     __name__                                     =                                     =                                     "__main__"                                     :                       
                                                 expr                                     =                                     "{()}[]"                       
           
                                                 # Function call                       
                                                 if                                     areBracketsBalanced(expr):                       
                                                 print                                     (                                     "Balanced"                                     )                       
                                                 else                                     :                       
                                                 print                                     (                                     "Not Balanced"                                     )                       
           
                         # This code is contributed by AnkitRai01 and improved                       
                         # by Raju Pitta                       

C#

                         // C# program for checking                       
                         // balanced Brackets                       
                         using                                     System;                       
                         using                                     System.Collections.Generic;                       
           
                         public                                     class                                     BalancedBrackets {                       
                                                 public                                     class                                     stack {                       
                                                 public                                     int                                     top = -1;                       
                                                 public                                     char                                     [] items =                                     new                                     char                                     [100];                       
           
                                                 public                                     void                                     push(                                     char                                     x)                       
                                                 {                       
                                                 if                                     (top == 99)                       
                                                 {                       
                                                 Console.WriteLine(                                     "Stack full"                                     );                       
                                                 }                       
                                                 else                                     {                       
                                                 items[++top] = x;                       
                                                 }                       
                                                 }                       
           
                                                 char                                     pop()                       
                                                 {                       
                                                 if                                     (top == -1)                       
                                                 {                       
                                                 Console.WriteLine(                                     "Underflow error"                                     );                       
                                                 return                                     ' '                                     ;                       
                                                 }                       
                                                 else                       
                                                 {                       
                                                 char                                     element = items[top];                       
                                                 top--;                       
                                                 return                                     element;                       
                                                 }                       
                                                 }                       
           
                                                 Boolean isEmpty()                       
                                                 {                       
                                                 return                                     (top == -1) ?                                     true                                     :                                     false                                     ;                       
                                                 }                       
                                                 }                       
           
                                                 // Returns true if character1 and character2                       
                                                 // are matching left and right brackets */                       
                                                 static                                     Boolean isMatchingPair(                                     char                                     character1,                       
                                                 char                                     character2)                       
                                                 {                       
                                                 if                                     (character1 ==                                     '('                                     && character2 ==                                     ')'                                     )                       
                                                 return                                     true                                     ;                       
                                                 else                                     if                                     (character1 ==                                     '{'                                     && character2 ==                                     '}'                                     )                       
                                                 return                                     true                                     ;                       
                                                 else                                     if                                     (character1 ==                                     '['                                     && character2 ==                                     ']'                                     )                       
                                                 return                                     true                                     ;                       
                                                 else                       
                                                 return                                     false                                     ;                       
                                                 }                       
           
                                                 // Return true if expression has balanced                       
                                                 // Brackets                       
                                                 static                                     Boolean areBracketsBalanced(                                     char                                     [] exp)                       
                                                 {                       
                                                 // Declare an empty character stack */                       
                                                 Stack<                                     char                                     > st =                                     new                                     Stack<                                     char                                     >();                       
           
                                                 // Traverse the given expression to                       
                                                 //   check matching brackets                       
                                                 for                                     (                                     int                                     i = 0; i < exp.Length; i++)                       
                                                 {                       
                                                 // If the exp[i] is a starting                       
                                                 // bracket then push it                       
                                                 if                                     (exp[i] ==                                     '{'                                     || exp[i] ==                                     '('                       
                                                 || exp[i] ==                                     '['                                     )                       
                                                 st.Push(exp[i]);                       
           
                                                 //  If exp[i] is an ending bracket                       
                                                 //  then pop from stack and check if the                       
                                                 //   popped bracket is a matching pair                       
                                                 if                                     (exp[i] ==                                     '}'                                     || exp[i] ==                                     ')'                       
                                                 || exp[i] ==                                     ']'                                     ) {                       
           
                                                 // If we see an ending bracket without                       
                                                 //   a pair then return false                       
                                                 if                                     (st.Count == 0)                       
                                                 {                       
                                                 return                                     false                                     ;                       
                                                 }                       
           
                                                 // Pop the top element from stack, if                       
                                                 // it is not a pair brackets of                       
                                                 // character then there is a mismatch. This                       
                                                 // happens for expressions like {(})                       
                                                 else                                     if                                     (!isMatchingPair(st.Pop(),                       
                                                 exp[i])) {                       
                                                 return                                     false                                     ;                       
                                                 }                       
                                                 }                       
                                                 }                       
           
                                                 // If there is something left in expression                       
                                                 // then there is a starting bracket without                       
                                                 // a closing bracket                       
           
                                                 if                                     (st.Count == 0)                       
                                                 return                                     true                                     ;                                     // balanced                       
                                                 else                       
                                                 {                       
                                                 // not balanced                       
                                                 return                                     false                                     ;                       
                                                 }                       
                                                 }                       
           
                                                 // Driver code                       
                                                 public                                     static                                     void                                     Main(String[] args)                       
                                                 {                       
                                                 char                                     [] exp = {                                     '{'                                     ,                                     '('                                     ,                                     ')'                                     ,                                     '}'                                     ,                                     '['                                     ,                                     ']'                                     };                       
           
                                                 // Function call                       
                                                 if                                     (areBracketsBalanced(exp))                       
                                                 Console.WriteLine(                                     "Balanced "                                     );                       
                                                 else                       
                                                 Console.WriteLine(                                     "Not Balanced "                                     );                       
                                                 }                       
                         }                       
           
                         // This code is contributed by 29AjayKumar                       

Javascript

                         <script>                       
           
                         // Javascript program for checking                       
                         // balanced brackets                       
           
                         // Function to check if brackets are balanced                       
                         function                                     areBracketsBalanced(expr)                       
                         {                       
                                   
                                                 // Using ArrayDeque is faster                       
                                                 // than using Stack class                       
                                                 let stack = [];                       
           
                                                 // Traversing the Expression                       
                                                 for                                     (let i = 0; i < expr.length; i++)                       
                                                 {                       
                                                 let x = expr[i];                       
           
                                                 if                                     (x ==                                     '('                                     || x ==                                     '['                                     || x ==                                     '{'                                     )                       
                                                 {                       
                                   
                                                 // Push the element in the stack                       
                                                 stack.push(x);                       
                                                 continue                                     ;                       
                                                 }                       
           
                                                 // If current character is not opening                       
                                                 // bracket, then it must be closing.                       
                                                 // So stack cannot be empty at this point.                       
                                                 if                                     (stack.length == 0)                       
                                                 return                                     false                                     ;                       
                                   
                                                 let check;                       
                                                 switch                                     (x){                       
                                                 case                                     ')'                                     :                       
                                                 check = stack.pop();                       
                                                 if                                     (check ==                                     '{'                                     || check ==                                     '['                                     )                       
                                                 return                                     false                                     ;                       
                                                 break                                     ;                       
           
                                                 case                                     '}'                                     :                       
                                                 check = stack.pop();                       
                                                 if                                     (check ==                                     '('                                     || check ==                                     '['                                     )                       
                                                 return                                     false                                     ;                       
                                                 break                                     ;                       
           
                                                 case                                     ']'                                     :                       
                                                 check = stack.pop();                       
                                                 if                                     (check ==                                     '('                                     || check ==                                     '{'                                     )                       
                                                 return                                     false                                     ;                       
                                                 break                                     ;                       
                                                 }                       
                                                 }                       
           
                                                 // Check Empty Stack                       
                                                 return                                     (stack.length == 0);                       
                         }                       
           
                         // Driver code                       
                         let expr =                                     "([{}])"                                     ;                       
           
                         // Function call                       
                         if                                     (areBracketsBalanced(expr))                       
                                                 document.write(                                     "Balanced "                                     );                       
                         else                       
                                                 document.write(                                     "Not Balanced "                                     );                       
           
                         // This code is contributed by rag2127                       
           
                         </script>                       

输出

Balanced

时间复杂性： O（n） 辅助空间： O（n）表示堆栈。

如果您在上述代码/算法中发现任何错误，请写下评论，或者寻找其他方法来解决相同的问题

文章版权归作者所有，未经允许请勿转载。

THE END

技术文章