带任意基b的数的补码-yiteyi-C++库

本文介绍了一种求任意基补码的通用方法 $b$ 本文对此进行了讨论。 寻找（b-1）补语的步骤 ：找到（b-1）的补语，

null

从带基数的数字系统中的最大数字中减去数字的每一位 $b$ .
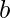例如，如果数字是以9为基数的三位数，则从888中减去该数字，因为8是以9为基数的数字系统中的最大数字。
得到的结果是（b-1）的（8的补码）补码。

寻找b的补码的步骤 ：要找到b的补码，只需在计算出的（b-1）补码中加1即可。现在，这适用于数字系统中存在的任何基数。它可以用1和2的补码来测试。实例 :

Let the number be 10111 base 2 (b=2)Then, 1's complement will be 01000 (b-1)2's complement will be 01001 (b)Taking a number with Octal base:Let the number be -456.Then 7's complement will be 321and 8's complement will be 322

推荐：请尝试你的方法 {IDE} 首先，在进入解决方案之前。

以下是上述理念的实施：

C++

                         // CPP program to find complement of a                       
                         // number with any base b                       
                         #include<iostream>                       
                         #include<cmath>                       
           
                         using                                     namespace                                     std;                       
           
                         // Function to find (b-1)'s complement                       
                         int                                     prevComplement(                                     int                                     n,                                     int                                     b)                       
                         {                       
                                                 int                                     maxDigit, maxNum = 0, digits = 0, num = n;                       
                                   
                                                 // Calculate number of digits                       
                                                 // in the given number                       
                                                 while                                     (n!=0)                       
                                                 {                       
                                                 digits++;                       
                                                 n = n/10;                       
                                                 }                       
                                   
                                                 // Largest digit in the number                       
                                                 // system with base b                       
                                                 maxDigit = b-1;                       
                                   
                                                 // Largest number in the number                       
                                                 // system with base b                       
                                                 while                                     (digits--)                       
                                                 {                       
                                                 maxNum = maxNum*10 + maxDigit;                       
                                                 }                       
                                   
                                                 // return Complement                       
                                                 return                                     maxNum - num;                       
                         }                       
           
                         // Function to find b's complement                       
                         int                                     complement(                                     int                                     n,                                     int                                     b)                       
                         {                       
                                                 // b's complement = (b-1)'s complement + 1                       
                                                 return                                     prevComplement(n,b) + 1;                       
                         }                       
           
                         // Driver code                       
                         int                                     main()                       
                         {                       
                                                 cout << prevComplement(25, 7)<<endl;                       
                                   
                                                 cout << complement(25, 7);                       
                                   
                                                 return                                     0;                       
                         }                       

JAVA

                         // Java program to find complement                       
                         // of a number with any base b                       
                         class                                     GFG                       
                         {                       
           
                         // Function to find (b-1)'s complement                       
                         static                                     int                                     prevComplement(                                     int                                     n,                                     int                                     b)                       
                         {                       
                                                 int                                     maxDigit, maxNum =                                     0                                     ,                       
                                                 digits =                                     0                                     , num = n;                       
                                   
                                                 // Calculate number of digits                       
                                                 // in the given number                       
                                                 while                                     (n !=                                     0                                     )                       
                                                 {                       
                                                 digits++;                       
                                                 n = n /                                     10                                     ;                       
                                                 }                       
                                   
                                                 // Largest digit in the number                       
                                                 // system with base b                       
                                                 maxDigit = b -                                     1                                     ;                       
                                   
                                                 // Largest number in the number                       
                                                 // system with base b                       
                                                 while                                     ((digits--) >                                     0                                     )                       
                                                 {                       
                                                 maxNum = maxNum *                                     10                                     + maxDigit;                       
                                                 }                       
                                   
                                                 // return Complement                       
                                                 return                                     maxNum - num;                       
                         }                       
           
                         // Function to find b's complement                       
                         static                                     int                                     complement(                                     int                                     n,                                     int                                     b)                       
                         {                       
                                                 // b's complement = (b-1)'s                       
                                                 // complement + 1                       
                                                 return                                     prevComplement(n, b) +                                     1                                     ;                       
                         }                       
           
                         // Driver code                       
                         public                                     static                                     void                                     main(String args[])                       
                         {                       
                                                 System.out.println(prevComplement(                                     25                                     ,                                     7                                     ));                       
                                   
                                                 System.out.println(complement(                                     25                                     ,                                     7                                     ));                       
                         }                       
                         }                       
           
                         // This code is contributed                       
                         // by Kirti_Mangal                       

Python 3

                         # Python 3 program to find                       
                         # complement of a number                       
                         # with any base b                       
           
                         # Function to find                       
                         # (b-1)'s complement                       
                         def                                     prevComplement(n, b) :                       
                                                 maxNum, digits, num                                     =                                     0                                     ,                                     0                                     , n                       
           
                                                 # Calculate number of digits                       
                                                 # in the given number                       
                                                 while                                     n >                                     1                                     :                       
                                                 digits                                     +                                     =                                     1                       
                                                 n                                     =                                     n                                     /                                     /                                     10                       
           
                                                 # Largest digit in the number                       
                                                 # system with base b                       
                                                 maxDigit                                     =                                     b                                     -                                     1                       
           
                                                 # Largest number in the number                       
                                                 # system with base b                       
                                                 while                                     digits :                       
                                                 maxNum                                     =                                     maxNum                                     *                                     10                                     +                                     maxDigit                       
                                                 digits                                     -                                     =                                     1                       
                                   
                                                 # return Complement                       
                                                 return                                     maxNum                                     -                                     num                       
           
                         # Function to find b's complement                       
                         def                                     complement(n, b) :                       
           
                                                 # b's complement = (b-1)'s                       
                                                 # complement + 1                       
                                                 return                                     prevComplement(n, b)                                     +                                     1                       
           
                         # Driver code                       
                         if                                     __name__                                     =                                     =                                     "__main__"                                     :                       
                                   
                                                 # Function calling                       
                                                 print                                     (prevComplement(                                     25                                     ,                                     7                                     ))                       
                                                 print                                     (complement(                                     25                                     ,                                     7                                     ))                       
           
                         # This code is contributed                       
                         # by ANKITRAI1                       

C#

                         // C# program to find complement                       
                         // of a number with any base b                       
                         class                                     GFG                       
                         {                       
           
                         // Function to find (b-1)'s complement                       
                         static                                     int                                     prevComplement(                                     int                                     n,                                     int                                     b)                       
                         {                       
                                                 int                                     maxDigit, maxNum = 0,                       
                                                 digits = 0, num = n;                       
                                   
                                                 // Calculate number of digits                       
                                                 // in the given number                       
                                                 while                                     (n != 0)                       
                                                 {                       
                                                 digits++;                       
                                                 n = n / 10;                       
                                                 }                       
                                   
                                                 // Largest digit in the number                       
                                                 // system with base b                       
                                                 maxDigit = b - 1;                       
                                   
                                                 // Largest number in the number                       
                                                 // system with base b                       
                                                 while                                     ((digits--) > 0)                       
                                                 {                       
                                                 maxNum = maxNum * 10 + maxDigit;                       
                                                 }                       
                                   
                                                 // return Complement                       
                                                 return                                     maxNum - num;                       
                         }                       
           
                         // Function to find b's complement                       
                         static                                     int                                     complement(                                     int                                     n,                                     int                                     b)                       
                         {                       
                                                 // b's complement = (b-1)'s                       
                                                 // complement + 1                       
                                                 return                                     prevComplement(n, b) + 1;                       
                         }                       
           
                         // Driver code                       
                         public                                     static                                     void                                     Main()                       
                         {                       
                                                 System.Console.WriteLine(prevComplement(25, 7));                       
                                   
                                                 System.Console.WriteLine(complement(25, 7));                       
                         }                       
                         }                       
           
                         // This code is contributed                       
                         // by mits                       

PHP

                         <?php                       
                         // PHP program to find complement                       
                         // of a number with any base b                       
           
                         // Function to find (b-1)'s complement                       
                         function                                     prevComplement(                                     $n                                     ,                                     $b                                     )                       
                         {                       
                                                 $maxNum                                     = 0;                       
                                                 $digits                                     = 0;                       
                                                 $num                                     =                                     $n                                     ;                       
                                   
                                                 // Calculate number of digits                       
                                                 // in the given number                       
                                                 while                                     ((int)                                     $n                                     != 0)                       
                                                 {                       
                                                 $digits                                     ++;                       
                                                 $n                                     =                                     $n                                     / 10;                       
                                                 }                       
                                   
                                                 // Largest digit in the number                       
                                                 // system with base b                       
                                                 $maxDigit                                     =                                     $b                                     - 1;                       
                                   
                                                 // Largest number in the number                       
                                                 // system with base b                       
                                                 while                                     (                                     $digits                                     --)                       
                                                 {                       
                                                 $maxNum                                     =                                     $maxNum                                     * 10 +                       
                                                 $maxDigit                                     ;                       
                                                 }                       
                                   
                                                 // return Complement                       
                                                 return                                     $maxNum                                     -                                     $num                                     ;                       
                         }                       
           
                         // Function to find b's complement                       
                         function                                     complement(                                     $n                                     ,                                     $b                                     )                       
                         {                       
                                                 // b's complement = (b-1)'s                       
                                                 // complement + 1                       
                                                 return                                     prevComplement(                                     $n                                     ,                                     $b                                     ) + 1;                       
                         }                       
           
                         // Driver code                       
                         echo                                     prevComplement(25, 7),                                     ""                                     ;                       
                                   
                         echo                                     (complement(25, 7));                       
           
                         // This code is contributed                       
                         // by Smitha                       
                         ?>                       

Javascript

                         <script>                       
           
                         // Javascript program to find complement                       
                         // of a number with any base b                       
           
                         // Function to find (b-1)'s complement                       
                                                 function                                     prevComplement(n , b) {                       
                                                 var                                     maxDigit, maxNum = 0, digits = 0,                       
                                                 num = n;                       
           
                                                 // Calculate number of digits                       
                                                 // in the given number                       
                                                 while                                     (n != 0) {                       
                                                 digits++;                       
                                                 n = parseInt(n / 10);                       
                                                 }                       
           
                                                 // Largest digit in the number                       
                                                 // system with base b                       
                                                 maxDigit = b - 1;                       
           
                                                 // Largest number in the number                       
                                                 // system with base b                       
                                                 while                                     ((digits--) > 0) {                       
                                                 maxNum = maxNum * 10 + maxDigit;                       
                                                 }                       
           
                                                 // return Complement                       
                                                 return                                     maxNum - num;                       
                                                 }                       
           
                                                 // Function to find b's complement                       
                                                 function                                     complement(n , b) {                       
                                                 // b's complement = (b-1)'s                       
                                                 // complement + 1                       
                                                 return                                     prevComplement(n, b) + 1;                       
                                                 }                       
           
                                                 // Driver code                       
                                   
                                                 document.write(prevComplement(25, 7)+                                     "<br/>"                                     );                       
           
                                                 document.write(complement(25, 7));                       
           
                         // This code is contributed by todaysgaurav                       
           
                         </script>                       

输出：

文章版权归作者所有，未经允许请勿转载。

THE END

技术文章