用二进制搜索计算n次实根-yiteyi-C++库

给定两个数x和n，求x的n次根。

null

例如：

输入： 5 2 输出： 2.2360679768025875

输入： x=5，n=3 输出： 1.70997594668

推荐：请尝试你的方法 {IDE} 首先，在进入解决方案之前。

为了计算n ^th 一个数字的根，我们可以使用以下程序。

如果x在这个范围内 [0, 1) 然后我们设定下限 低=x 和上限 高=1 ，因为对于这个数字范围，n次方根总是大于给定的数字，并且永远不能超过1。例如- $$sqrt{0.09} = 0.3$.$
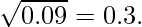
否则，我们就采取行动 低=1 和 高=x .
声明一个名为 ε 并根据需要对其进行初始化。假设epsilon=0.01，那么我们可以保证对给定数字的n次方根的猜测是最多更正2位小数。
声明一个变量guess并将其初始化为 猜测=（低+高）/2。
运行循环，以便：
- 如果 绝对误差 我们的猜测不仅仅是 ε 然后做：
  1. 如果 猜测 ^N >x 然后猜
  2. 其他的 低=猜测
  3. 让一个新的更好猜测即。， 猜测=（低+高）/2。
- 如果 绝对误差 我们的猜测小于ε，则退出循环。

绝对误差： 绝对误差可计算为： 腹肌（猜测） ^N -十）

C++

                         // C++ Program to find                       
                         // n-th real root of x                       
                         #include <bits/stdc++.h>                       
                         using                                     namespace                                     std;                       
           
                         void                                     findNthRoot(                                     double                                     x,                                     int                                     n)                       
                         {                       
           
                                                 // Initialize boundary values                       
                                                 double                                     low, high;                       
                                                 if                                     (x >= 0 and x <= 1)                       
                                                 {                       
                                                 low = x;                       
                                                 high = 1;                       
                                                 }                       
                                                 else                       
                                                 {                       
                                                 low = 1;                       
                                                 high = x;                       
                                                 }                       
           
                                                 // Used for taking approximations                       
                                                 // of the answer                       
                                                 double                                     epsilon = 0.00000001;                       
           
                                                 // Do binary search                       
                                                 double                                     guess = (low + high) / 2;                       
                                                 while                                     (                                     abs                                     ((                                     pow                                     (guess, n)) - x) >= epsilon)                       
                                                 {                       
                                                 if                                     (                                     pow                                     (guess, n) > x)                       
                                                 {                       
                                                 high = guess;                       
                                                 }                       
                                                 else                       
                                                 {                       
                                                 low = guess;                       
                                                 }                       
                                                 guess = (low + high) / 2;                       
                                                 }                       
           
                                                 cout << fixed << setprecision(16) << guess;                       
                         }                       
           
                         // Driver code                       
                         int                                     main()                       
                         {                       
                                                 double                                     x = 5;                       
                                                 int                                     n = 2;                       
                                                 findNthRoot(x, n);                       
                         }                       
           
                         // This code is contributed                       
                         // by Subhadeep                       

JAVA

                         // Java Program to find n-th real root of x                       
                         class                                     GFG                       
                         {                       
                                                 static                                     void                                     findNthRoot(                                     double                                     x,                                     int                                     n)                       
                                                 {                       
           
                                                 // Initialize boundary values                       
                                                 double                                     low, high;                       
                                                 if                                     (x >=                                     0                                     && x <=                                     1                                     )                       
                                                 {                       
                                                 low = x;                       
                                                 high =                                     1                                     ;                       
                                                 }                       
                                                 else                       
                                                 {                       
                                                 low =                                     1                                     ;                       
                                                 high = x;                       
                                                 }                       
           
                                                 // used for taking approximations                       
                                                 // of the answer                       
                                                 double                                     epsilon =                                     0.00000001                                     ;                       
           
                                                 // Do binary search                       
                                                 double                                     guess = (low + high) /                                     2                                     ;                       
                                                 while                                     (Math.abs((Math.pow(guess, n)) - x)                       
                                                 >= epsilon)                       
                                                 {                       
                                                 if                                     (Math.pow(guess, n) > x)                       
                                                 {                       
                                                 high = guess;                       
                                                 }                       
                                                 else                       
                                                 {                       
                                                 low = guess;                       
                                                 }                       
                                                 guess = (low + high) /                                     2                                     ;                       
                                                 }                       
           
                                                 System.out.println(guess);                       
                                                 }                       
           
                                                 // Driver code                       
                                                 public                                     static                                     void                                     main(String[] args)                       
                                                 {                       
                                                 double                                     x =                                     5                                     ;                       
                                                 int                                     n =                                     2                                     ;                       
                                                 findNthRoot(x, n);                       
                                                 }                       
                         }                       
           
                         // This code is contributed                       
                         // by mits                       

Python3

                         # Python Program to find n-th real root                       
                         # of x                       
           
           
                         def                                     findNthRoot(x, n):                       
           
                                                 # Initialize boundary values                       
                                                 x                                     =                                     float                                     (x)                       
                                                 n                                     =                                     int                                     (n)                       
                                                 if                                     (x >                                     =                                     0                                     and                                     x <                                     =                                     1                                     ):                       
                                                 low                                     =                                     x                       
                                                 high                                     =                                     1                       
                                                 else                                     :                       
                                                 low                                     =                                     1                       
                                                 high                                     =                                     x                       
           
                                                 # used for taking approximations                       
                                                 # of the answer                       
                                                 epsilon                                     =                                     0.00000001                       
           
                                                 # Do binary search                       
                                                 guess                                     =                                     (low                                     +                                     high)                                     /                                     2                       
                                                 while                                     abs                                     (guess                                     *                                     *                                     n                                     -                                     x) >                                     =                                     epsilon:                       
                                                 if                                     guess                                     *                                     *                                     n > x:                       
                                                 high                                     =                                     guess                       
                                                 else                                     :                       
                                                 low                                     =                                     guess                       
                                                 guess                                     =                                     (low                                     +                                     high)                                     /                                     2                       
                                                 print                                     (guess)                       
           
           
                         # Driver code                       
                         x                                     =                                     5                       
                         n                                     =                                     2                       
                         findNthRoot(x, n)                       

C#

                         // C# Program to find n-th real root of x                       
           
                         using                                     System;                       
           
                         public                                     class                                     GFG {                       
                                                 static                                     void                                     findNthRoot(                                     double                                     x,                                     int                                     n)                       
                                                 {                       
           
                                                 // Initialize boundary values                       
                                                 double                                     low, high;                       
                                                 if                                     (x >= 0 && x <= 1)                       
                                                 {                       
                                                 low = x;                       
                                                 high = 1;                       
                                                 }                       
                                                 else                       
                                                 {                       
                                                 low = 1;                       
                                                 high = x;                       
                                                 }                       
           
                                                 // used for taking approximations                       
                                                 // of the answer                       
                                                 double                                     epsilon = 0.00000001;                       
           
                                                 // Do binary search                       
                                                 double                                     guess = (low + high) / 2;                       
                                                 while                                     (Math.Abs((Math.Pow(guess, n)) - x)                       
                                                 >= epsilon)                       
                                                 {                       
                                                 if                                     (Math.Pow(guess, n) > x)                       
                                                 {                       
                                                 high = guess;                       
                                                 }                       
                                                 else                       
                                                 {                       
                                                 low = guess;                       
                                                 }                       
                                                 guess = (low + high) / 2;                       
                                                 }                       
           
                                                 Console.WriteLine(guess);                       
                                                 }                       
           
                                                 // Driver code                       
                                                 static                                     public                                     void                                     Main()                       
                                                 {                       
                                                 double                                     x = 5;                       
                                                 int                                     n = 2;                       
                                                 findNthRoot(x, n);                       
                                                 }                       
                         }                       
           
                         // This code is contributed by akt_mit                       

Javascript

                         <script>                       
           
                                                 // Javascript Program to find n-th                       
                                                 // real root of x                       
                                   
                                                 function                                     findNthRoot(x, n)                       
                                                 {                       
                                   
                                                 // Initialize boundary values                       
                                                 let low, high;                       
                                                 if                                     (x >= 0 && x <= 1)                       
                                                 {                       
                                                 low = x;                       
                                                 high = 1;                       
                                                 }                       
                                                 else                       
                                                 {                       
                                                 low = 1;                       
                                                 high = x;                       
                                                 }                       
                                   
                                                 // used for taking approximations                       
                                                 // of the answer                       
                                                 let epsilon = 0.00000001;                       
                                   
                                                 // Do binary search                       
                                                 let guess = parseInt((low + high) / 2, 10);                       
                                                 while                                     (Math.abs((Math.pow(guess, n)) - x)                       
                                                 >= epsilon)                       
                                                 {                       
                                                 if                                     (Math.pow(guess, n) > x)                       
                                                 {                       
                                                 high = guess;                       
                                                 }                       
                                                 else                       
                                                 {                       
                                                 low = guess;                       
                                                 }                       
                                                 guess = (low + high) / 2;                       
                                                 }                       
                                   
                                                 document.write(guess);                       
                                                 }                       
                                   
                                                 let x = 5;                       
                                                 let n = 2;                       
                                                 findNthRoot(x, n);                       
                                   
                         </script>                       

输出

2.2360679768025875

用ε=0.01解释第一个示例

Since taking too small value of epsilon as taken in our program might not be feasible forexplanation because it will increase the number of steps drastically so for the sake ofsimplicity we are taking epsilon = 0.01The above procedure will work as follows:Say we have to calculate the then x = 5, low = 1, high = 5.Taking epsilon = 0.01First Guess:guess = (1 + 5) / 2 = 3Absolute error = |3² - 5| = 4 > epsilonguess² = 9 > 5(x) then high = guess --> high = 3Second Guess:guess = (1 + 3) / 2 = 2Absolute error = |2² - 5| = 1 > epsilonguess² = 4 > 5(x) then low = guess --> low = 2Third Guess:guess = (2 + 3) / 2 = 2.5Absolute error = |2.5² - 5| = 1.25 > epsilonguess² = 6.25 > 5(x) then high = guess --> high = 2.5and proceeding so on we will get the  correct up to 2 decimal places i.e.,  = 2.23600456We will ignore the digits after 2 decimal places since they may or may not be correct.

文章版权归作者所有，未经允许请勿转载。

THE END

技术文章