先决条件: 母函数 , 斐波那契数 , 斐波那契数的求法 .
使用方法 母函数 解决著名和有用的问题 斐波那契数 “这篇文章讨论了复发问题。
这个 生成函数 是解决各种数学问题的有力工具,包括计数问题。这是一个正式的权力系列。例如,在计算问题时,我们通常感兴趣的是找到大小物体的数量 ![]() 在这种情况下,我们定义了一个幂级数,简单来说,它是一个无限项多项式,其中
在这种情况下,我们定义了一个幂级数,简单来说,它是一个无限项多项式,其中 ![]() 学位术语是
学位术语是 ![]() 序列的项。这有助于我们找到许多有趣而重要的结果。应该注意的是,在使用生成函数时,我们通常使用生成函数幂级数中的系数,很少使用级数中的变量。在这篇文章中,我们也将这样做。一类a的普通母函数 N 是:
序列的项。这有助于我们找到许多有趣而重要的结果。应该注意的是,在使用生成函数时,我们通常使用生成函数幂级数中的系数,很少使用级数中的变量。在这篇文章中,我们也将这样做。一类a的普通母函数 N 是:
斐波那契数 是数学中的基本序列之一,人们已经发现了许多方法来找出这个序列的高阶项。这篇文章讨论了这样一种方法。
让我们首先为斐波那契数定义一个生成函数,然后将该函数简化为一个递归。利用这一点,扩展简化并将其分解为部分分数,然后使用两个标准幂级数,然后将它们结合起来,以获得令人惊讶的结果 ![]() 斐波那契级数的项。
斐波那契级数的项。
让我们定义生成函数 ![]() 像
像
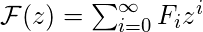
,
哪里
是第i个斐波那契数。
自从
![]() .
.
![]() .
.
重新安排他们,
![]() .
.
以通用术语来说,
![]()
![]()
进一步简化,得到以下函数。
![]() .
.
解决 ![]() ,我们得到:
,我们得到:
![]() .
.
通过以上运算,我们得到以下公式:
,
哪里
和
.
因此
![]() 还要注意,
还要注意,
![]() .
.
因此,将这个关系保持在上面的表达式中,我们得到,
![]() .
.
现在,上面表达式的右边可以分成部分分数,
![Rendered by QuickLaTeX.com mathcal{F}(z) = frac{1}{sqrt{5}}left [ frac{1}{(1-phi z)} - frac{1}{(1-widehat{phi} z)}
ight ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-399ddde8c421a3f0766584f1a31b9c05_l3.png) .
.
使用 膨胀 在这两个分数上,
![]() .
.
同样地,
![]() .
.
因此
![]() .
.
因此
![]() .
.
现在
![]() ,
,
和
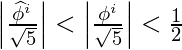
利用以上两个事实,我们可以得出如下结论:
,四舍五入到最接近的整数。
用黄金分割比求n次斐波那契数 是这个公式的应用之一。


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



