半径为R的圆中的矩形数-yiteyi-C++库

给定半径为R的圆片，任务是求出长度和宽度为整数的矩形的总数，每次一个。 例如：

null

输入：R=2 输出 : 8 8个矩形可以从半径为2的圆形薄板上切割。它们是：1×1，1×2，2×1，2×2，1×3，3×1，2×3，3×2。输入：R=1 输出 : 1 只能有一个尺寸为1 X 1的矩形。

方法考虑下面的图表，

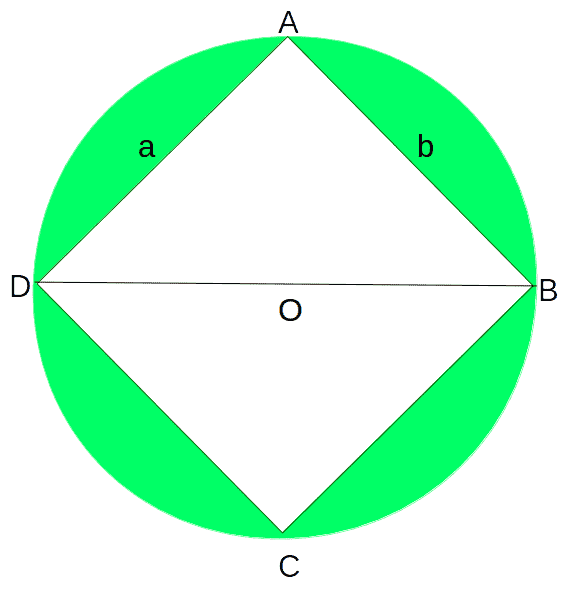
Circle_largest_rect

很容易看出，ABCD是给定半径圆中可以形成的最大矩形 R 和中心O，有尺寸 a X b 放下一个垂直的AO，这样， ∠AOD=∠AOB=90° 考虑下面的图表进行进一步的分析，

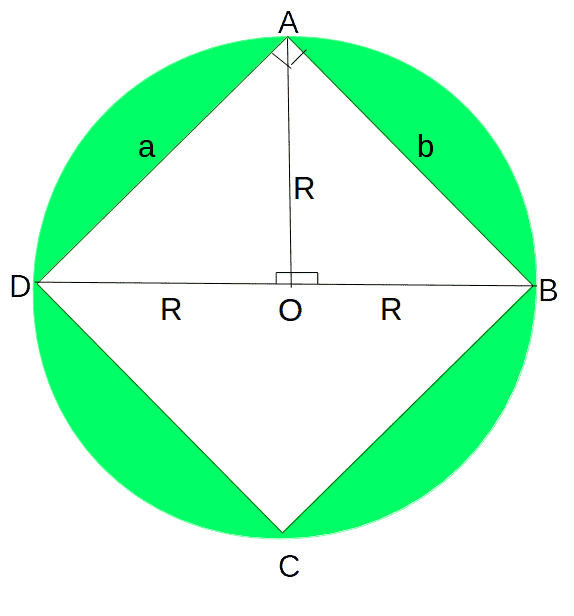
rectange_circle_square_proof

Consider triangles AOD and AOB,In these triangles,AO = AO (Common Side)∠AOD = ∠AOB = 90° OD = OB = RThus, by SAS congruence ▵AOD ≅ ▵AOB∴ AD = AB by CPCT(i.e Corresponding Parts on Congruent Triangles)or, a = b=> The rectangle ABCD is a square

直径BD是从圆形薄板上切割矩形所需的最大对角线。因此，可以检查a和b的所有组合以形成所有可能的矩形，并且如果任何此类矩形的对角线小于或等于形成的最大矩形的对角线长度（即2*R，其中R是如上所述的圆的半径）现在，a和b的最大长度将始终严格小于圆的直径，因此a和b的所有可能值将位于闭合区间[1，（2*R–1）]。以下是上述方法的实施情况：

C++

                         // C++ program to find the number of rectangles                       
                         // that can be cut from a circle of Radius R                       
                         #include <bits/stdc++.h>                       
                         using                                     namespace                                     std;                       
           
                         // Function to return the total possible                       
                         // rectangles that can be cut from the circle                       
                         int                                     countRectangles(                                     int                                     radius)                       
                         {                       
           
                                                 int                                     rectangles = 0;                       
           
                                                 // Diameter = 2 * Radius                       
                                                 int                                     diameter = 2 * radius;                       
           
                                                 // Square of diameter which is the square                       
                                                 // of the maximum length diagonal                       
                                                 int                                     diameterSquare = diameter * diameter;                       
           
                                                 // generate all combinations of a and b                       
                                                 // in the range (1, (2 * Radius - 1))(Both inclusive)                       
                                                 for                                     (                                     int                                     a = 1; a < 2 * radius; a++) {                       
                                                 for                                     (                                     int                                     b = 1; b < 2 * radius; b++) {                       
           
                                                 // Calculate the Diagonal length of                       
                                                 // this rectangle                       
                                                 int                                     diagonalLengthSquare = (a * a + b * b);                       
           
                                                 // If this rectangle's Diagonal Length                       
                                                 // is less than the Diameter, it is a                       
                                                 // valid rectangle, thus increment counter                       
                                                 if                                     (diagonalLengthSquare <= diameterSquare) {                       
                                                 rectangles++;                       
                                                 }                       
                                                 }                       
                                                 }                       
           
                                                 return                                     rectangles;                       
                         }                       
           
                         // Driver Code                       
                         int                                     main()                       
                         {                       
           
                                                 // Radius of the circle                       
                                                 int                                     radius = 2;                       
           
                                                 int                                     totalRectangles;                       
                                                 totalRectangles = countRectangles(radius);                       
                                                 cout << totalRectangles <<                                     " rectangles can be"                       
                                                 <<                                     "cut from a circle of Radius "                                     << radius;                       
                                                 return                                     0;                       
                         }                       

JAVA

                         // Java program to find the                       
                         // number of rectangles that                       
                         // can be cut from a circle                       
                         // of Radius R                       
                         import                                     java.io.*;                       
           
                         class                                     GFG                       
                         {                       
                                   
                         // Function to return                       
                         // the total possible                       
                         // rectangles that can                       
                         // be cut from the circle                       
                         static                                     int                                     countRectangles(                                     int                                     radius)                       
                         {                       
                                                 int                                     rectangles =                                     0                                     ;                       
           
                                                 // Diameter = 2 * Radius                       
                                                 int                                     diameter =                                     2                                     * radius;                       
           
                                                 // Square of diameter                       
                                                 // which is the square                       
                                                 // of the maximum length                       
                                                 // diagonal                       
                                                 int                                     diameterSquare = diameter *                       
                                                 diameter;                       
           
                                                 // generate all combinations                       
                                                 // of a and b in the range                       
                                                 // (1, (2 * Radius - 1))                       
                                                 // (Both inclusive)                       
                                                 for                                     (                                     int                                     a =                                     1                                     ;                       
                                                 a <                                     2                                     * radius; a++)                       
                                                 {                       
                                                 for                                     (                                     int                                     b =                                     1                                     ;                       
                                                 b <                                     2                                     * radius; b++)                       
                                                 {                       
           
                                                 // Calculate the                       
                                                 // Diagonal length of                       
                                                 // this rectangle                       
                                                 int                                     diagonalLengthSquare = (a * a +                       
                                                 b * b);                       
           
                                                 // If this rectangle's Diagonal                       
                                                 // Length is less than the Diameter,                       
                                                 // it is a valid rectangle, thus                       
                                                 // increment counter                       
                                                 if                                     (diagonalLengthSquare <= diameterSquare)                       
                                                 {                       
                                                 rectangles++;                       
                                                 }                       
                                                 }                       
                                                 }                       
           
                                                 return                                     rectangles;                       
                         }                       
           
                         // Driver Code                       
                         public                                     static                                     void                                     main (String[] args)                       
                         {                       
                                   
                         // Radius of the circle                       
                         int                                     radius =                                     2                                     ;                       
           
                         int                                     totalRectangles;                       
                         totalRectangles = countRectangles(radius);                       
                         System.out.println(totalRectangles +                       
                                                 " rectangles can be "                                     +                       
                                                 "cut from a circle of"                                     +                       
                                                 " Radius "                                     + radius);                       
                         }                       
                         }                       
           
                         // This code is contributed                       
                         // by anuj_67.                       

Python3

                         # Python3 program to find                       
                         # the number of rectangles                       
                         # that can be cut from a                       
                         # circle of Radius R Function                       
                         # to return the total possible                       
                         # rectangles that can be cut                       
                         # from the circle                       
                         def                                     countRectangles(radius):                       
                                   
                                                 rectangles                                     =                                     0                       
                                   
                                                 # Diameter = 2 * Radius                       
                                                 diameter                                     =                                     2                                     *                                     radius                       
                                   
                                                 # Square of diameter which                       
                                                 # is the square of the                       
                                                 # maximum length diagonal                       
                                                 diameterSquare                                     =                                     diameter                                     *                                     diameter                       
                                   
                                                 # generate all combinations                       
                                                 # of a and b in the range                       
                                                 # (1, (2 * Radius - 1))(Both inclusive)                       
                                                 for                                     a                                     in                                     range                                     (                                     1                                     ,                                     2                                     *                                     radius):                       
                                                 for                                     b                                     in                                     range                                     (                                     1                                     ,                                     2                                     *                                     radius):                       
                                   
                                                 # Calculate the Diagonal                       
                                                 # length of this rectangle                       
                                                 diagonalLengthSquare                                     =                                     (a                                     *                                     a                                     +                       
                                                 b                                     *                                     b)                       
                                   
                                                 # If this rectangle's Diagonal                       
                                                 # Length is less than the                       
                                                 # Diameter, it is a valid                       
                                                 # rectangle, thus increment counter                       
                                                 if                                     (diagonalLengthSquare <                                     =                                     diameterSquare) :                       
                                                 rectangles                                     +                                     =                                     1                       
                                   
                                                 return                                     rectangles                       
           
                         # Driver Code                       
           
                         # Radius of the circle                       
                         radius                                     =                                     2                       
                         totalRectangles                                     =                                     countRectangles(radius)                       
                         print                                     (totalRectangles ,                                     "rectangles can be"                                     ,                       
                                                 "cut from a circle of Radius"                                     , radius)                       
           
                         # This code is contributed by Smita                       

C#

                         // C# program to find the                       
                         // number of rectangles that                       
                         // can be cut from a circle                       
                         // of Radius R                       
                         using                                     System;                       
           
                         class                                     GFG                       
                         {                       
                                   
                         // Function to return                       
                         // the total possible                       
                         // rectangles that can                       
                         // be cut from the circle                       
                         static                                     int                                     countRectangles(                                     int                                     radius)                       
                         {                       
                                                 int                                     rectangles = 0;                       
           
                                                 // Diameter = 2 * Radius                       
                                                 int                                     diameter = 2 * radius;                       
           
                                                 // Square of diameter                       
                                                 // which is the square                       
                                                 // of the maximum length                       
                                                 // diagonal                       
                                                 int                                     diameterSquare = diameter *                       
                                                 diameter;                       
           
                                                 // generate all combinations                       
                                                 // of a and b in the range                       
                                                 // (1, (2 * Radius - 1))                       
                                                 // (Both inclusive)                       
                                                 for                                     (                                     int                                     a = 1;                       
                                                 a < 2 * radius; a++)                       
                                                 {                       
                                                 for                                     (                                     int                                     b = 1;                       
                                                 b < 2 * radius; b++)                       
                                                 {                       
           
                                                 // Calculate the                       
                                                 // Diagonal length of                       
                                                 // this rectangle                       
                                                 int                                     diagonalLengthSquare = (a * a +                       
                                                 b * b);                       
           
                                                 // If this rectangle's                       
                                                 // Diagonal Length is                       
                                                 // less than the Diameter,                       
                                                 // it is a valid rectangle,                       
                                                 // thus increment counter                       
                                                 if                                     (diagonalLengthSquare <=                       
                                                 diameterSquare)                       
                                                 {                       
                                                 rectangles++;                       
                                                 }                       
                                                 }                       
                                                 }                       
           
                                                 return                                     rectangles;                       
                         }                       
           
                         // Driver Code                       
                         public                                     static                                     void                                     Main ()                       
                         {                       
                                   
                         // Radius of the circle                       
                         int                                     radius = 2;                       
           
                         int                                     totalRectangles;                       
                         totalRectangles = countRectangles(radius);                       
                         Console.WriteLine(totalRectangles +                       
                                                 " rectangles can be "                                     +                       
                                                 "cut from a circle of"                                     +                       
                                                 " Radius "                                     + radius);                       
                         }                       
                         }                       
           
                         // This code is contributed                       
                         // by anuj_67.                       

PHP

                         <?php                       
                         // PHP program to find the                       
                         // number of rectangles that                       
                         // can be cut from a circle                       
                         // of Radius R                       
           
                         // Function to return the                       
                         // total possible rectangles                       
                         // that can be cut from the circle                       
                         function                                     countRectangles(                                     $radius                                     )                       
                         {                       
           
                                                 $rectangles                                     = 0;                       
           
                                                 // Diameter = 2 * $Radius                       
                                                 $diameter                                     = 2 *                                     $radius                                     ;                       
           
                                                 // Square of diameter which                       
                                                 // is the square of the                       
                                                 // maximum length diagonal                       
                                                 $diameterSquare                                     =                                     $diameter                                     *                       
                                                 $diameter                                     ;                       
           
                                                 // generate all combinations                       
                                                 // of a and b in the range                       
                                                 // (1, (2 * Radius - 1))(Both inclusive)                       
                                                 for                                     (                                     $a                                     = 1;                       
                                                 $a                                     < 2 *                                     $radius                                     ;                                     $a                                     ++)                       
                                                 {                       
                                                 for                                     (                                     $b                                     = 1;                       
                                                 $b                                     < 2 *                                     $radius                                     ;                                     $b                                     ++)                       
                                                 {                       
           
                                                 // Calculate the Diagonal                       
                                                 // length of this rectangle                       
                                                 $diagonalLengthSquare                                     = (                                     $a                                     *                                     $a                                     +                       
                                                 $b                                     *                                     $b                                     );                       
           
                                                 // If this rectangle's Diagonal                       
                                                 // Length is less than the                       
                                                 // Diameter, it is a valid                       
                                                 // rectangle, thus increment counter                       
                                                 if                                     (                                     $diagonalLengthSquare                                     <=                                     $diameterSquare                                     )                       
                                                 {                       
                                                 $rectangles                                     ++;                       
                                                 }                       
                                                 }                       
                                                 }                       
           
                                                 return                                     $rectangles                                     ;                       
                         }                       
           
                         // Driver Code                       
           
                         // Radius of the circle                       
                         $radius                                     = 2;                       
           
                         $totalRectangles                                     ;                       
                         $totalRectangles                                     = countRectangles(                                     $radius                                     );                       
                         echo                                     $totalRectangles                                     ,                                     " rectangles can be "                                     ,                       
                                                 "cut from a circle of Radius "                                     ,                                     $radius                                     ;                       
           
                         // This code is contributed                       
                         // by anuj_67.                       
                         ?>                       

Javascript

                         <script>                       
                         // java script  program to find the                       
                         // number of rectangles that                       
                         // can be cut from a circle                       
                         // of Radius R                       
           
                         // Function to return the                       
                         // total possible rectangles                       
                         // that can be cut from the circle                       
                         function                                     countRectangles(radius)                       
                         {                       
           
                                                 let rectangles = 0;                       
           
                                                 // Diameter = 2 * $Radius                       
                                                 let diameter = 2 * radius;                       
           
                                                 // Square of diameter which                       
                                                 // is the square of the                       
                                                 // maximum length diagonal                       
                                                 let diameterSquare = diameter *                       
                                                 diameter;                       
           
                                                 // generate all combinations                       
                                                 // of a and b in the range                       
                                                 // (1, (2 * Radius - 1))(Both inclusive)                       
                                                 for                                     (let a = 1;a < 2 * radius; a++)                       
                                                 {                       
                                                 for                                     (let b = 1;                       
                                                 b < 2 * radius; b++)                       
                                                 {                       
           
                                                 // Calculate the Diagonal                       
                                                 // length of this rectangle                       
                                                 let diagonalLengthSquare = (a * a +                       
                                                 b * b);                       
           
                                                 // If this rectangle's Diagonal                       
                                                 // Length is less than the                       
                                                 // Diameter, it is a valid                       
                                                 // rectangle, thus increment counter                       
                                                 if                                     (diagonalLengthSquare <= diameterSquare)                       
                                                 {                       
                                                 rectangles++;                       
                                                 }                       
                                                 }                       
                                                 }                       
           
                                                 return                                     rectangles;                       
                         }                       
           
                         // Driver Code                       
           
                         // Radius of the circle                       
                         let radius = 2;                       
           
                         let totalRectangles;                       
                         totalRectangles = countRectangles(radius);                       
                         document.write( totalRectangles +                                     " rectangles can be cut from a circle of Radius "                                     +radius);                       
           
                         // This code is contributed by sravan kumar                       
                         </script>                       

输出：

8 rectangles can be cut from a circle of Radius 2

时间复杂性： O（R） ^2. )，其中R是圆的半径

文章版权归作者所有，未经允许请勿转载。

THE END

技术文章