给出无向图的邻接矩阵表示。看看有没有 欧拉路径 在图表中。如果没有路径,则打印“无解决方案”。如果有路径,请打印路径。
null
例如:
Input : [[0, 1, 0, 0, 1],
[1, 0, 1, 1, 0],
[0, 1, 0, 1, 0],
[0, 1, 1, 0, 0],
[1, 0, 0, 0, 0]]
Output : 5 -> 1 -> 2 -> 4 -> 3 -> 2
Input : [[0, 1, 0, 1, 1],
[1, 0, 1, 0, 1],
[0, 1, 0, 1, 1],
[1, 1, 1, 0, 0],
[1, 0, 1, 0, 0]]
Output : "No Solution"
该问题的基本情况是,如果边数奇数(即奇数度)的顶点数大于2,则不存在欧拉路径。 如果它有解,并且所有节点都有偶数条边,那么我们可以从任何节点开始我们的路径。 如果它有解,并且正好有两个顶点有奇数条边,那么我们必须从这两个顶点中的一个开始我们的路径。 不会出现只有一个顶点有奇数条边的情况,因为总共有偶数条边。
查找路径的过程:
- 首先,获取一个空堆栈和一个空路径。
- 如果所有顶点都有偶数条边,则从其中任何一条开始。如果其中两个顶点有奇数条边,则从其中一条开始。将变量current设置为此起始顶点。
- 如果当前顶点至少有一个相邻节点,则首先发现该节点,然后通过回溯发现当前节点。要执行此操作,请将当前节点添加到堆栈中,删除当前节点和邻居节点之间的边,将当前设置为邻居节点。
- 如果当前节点没有任何邻居,则将其添加到路径和弹出堆栈中,并将当前设置为弹出顶点。
- 重复过程3和4,直到堆栈为空且当前节点没有任何邻居。
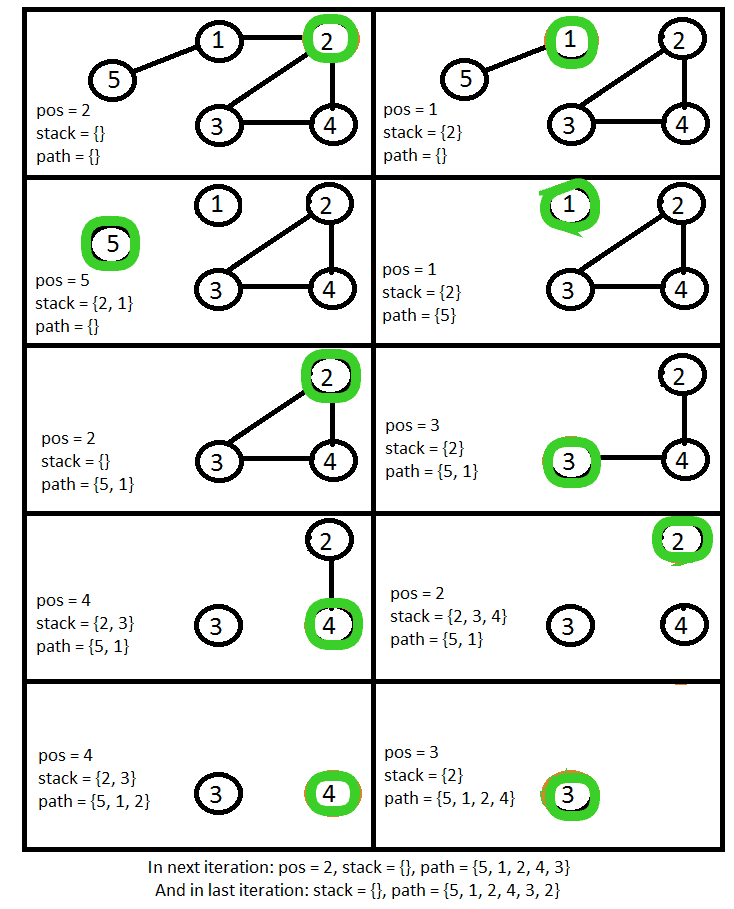
进程路径变量保持欧拉路径之后。
C++
// Efficient C++ program to // find out Eulerian path #include <bits/stdc++.h> using namespace std; // Function to find out the path // It takes the adjacency matrix // representation of the graph as input void findpath( int graph[][5], int n) { vector< int > numofadj; // Find out number of edges each vertex has for ( int i = 0; i < n; i++) numofadj.push_back(accumulate(graph[i], graph[i] + 5, 0)); // Find out how many vertex has odd number edges int startpoint = 0, numofodd = 0; for ( int i = n - 1; i >= 0; i--) { if (numofadj[i] % 2 == 1) { numofodd++; startpoint = i; } } // If number of vertex with odd number of edges // is greater than two return "No Solution". if (numofodd > 2) { cout << "No Solution" << endl; return ; } // If there is a path find the path // Initialize empty stack and path // take the starting current as discussed stack< int > stack; vector< int > path; int cur = startpoint; // Loop will run until there is element in the stack // or current edge has some neighbour. while (!stack.empty() or accumulate(graph[cur], graph[cur] + 5, 0) != 0) { // If current node has not any neighbour // add it to path and pop stack // set new current to the popped element if (accumulate(graph[cur], graph[cur] + 5, 0) == 0) { path.push_back(cur); cur = stack.top(); stack.pop(); } // If the current vertex has at least one // neighbour add the current vertex to stack, // remove the edge between them and set the // current to its neighbour. else { for ( int i = 0; i < n; i++) { if (graph[cur][i] == 1) { stack.push(cur); graph[cur][i] = 0; graph[i][cur] = 0; cur = i; break ; } } } } // print the path for ( auto ele : path) cout << ele << " -> " ; cout << cur << endl; } // Driver Code int main() { // Test case 1 int graph1[][5] = {{0, 1, 0, 0, 1}, {1, 0, 1, 1, 0}, {0, 1, 0, 1, 0}, {0, 1, 1, 0, 0}, {1, 0, 0, 0, 0}}; int n = sizeof (graph1) / sizeof (graph1[0]); findpath(graph1, n); // Test case 2 int graph2[][5] = {{0, 1, 0, 1, 1}, {1, 0, 1, 0, 1}, {0, 1, 0, 1, 1}, {1, 1, 1, 0, 0}, {1, 0, 1, 0, 0}}; n = sizeof (graph1) / sizeof (graph1[0]); findpath(graph2, n); // Test case 3 int graph3[][5] = {{0, 1, 0, 0, 1}, {1, 0, 1, 1, 1}, {0, 1, 0, 1, 0}, {0, 1, 1, 0, 1}, {1, 1, 0, 1, 0}}; n = sizeof (graph1) / sizeof (graph1[0]); findpath(graph3, n); } // This code is contributed by // sanjeev2552 |
JAVA
// Efficient Java program to // find out Eulerian path import java.util.*; class GFG { // Function to find out the path // It takes the adjacency matrix // representation of the graph as input static void findpath( int [][] graph, int n) { Vector<Integer> numofadj = new Vector<>(); // Find out number of edges each vertex has for ( int i = 0 ; i < n; i++) numofadj.add(accumulate(graph[i], 0 )); // Find out how many vertex has odd number edges int startPoint = 0 , numofodd = 0 ; for ( int i = n - 1 ; i >= 0 ; i--) { if (numofadj.elementAt(i) % 2 == 1 ) { numofodd++; startPoint = i; } } // If number of vertex with odd number of edges // is greater than two return "No Solution". if (numofodd > 2 ) { System.out.println( "No Solution" ); return ; } // If there is a path find the path // Initialize empty stack and path // take the starting current as discussed Stack<Integer> stack = new Stack<>(); Vector<Integer> path = new Vector<>(); int cur = startPoint; // Loop will run until there is element in the stack // or current edge has some neighbour. while (!stack.isEmpty() || accumulate(graph[cur], 0 ) != 0 ) { // If current node has not any neighbour // add it to path and pop stack // set new current to the popped element if (accumulate(graph[cur], 0 ) == 0 ) { path.add(cur); cur = stack.pop(); // If the current vertex has at least one // neighbour add the current vertex to stack, // remove the edge between them and set the // current to its neighbour. } else { for ( int i = 0 ; i < n; i++) { if (graph[cur][i] == 1 ) { stack.add(cur); graph[cur][i] = 0 ; graph[i][cur] = 0 ; cur = i; break ; } } } } // print the path for ( int ele : path) System.out.print(ele + " -> " ); System.out.println(cur); } static int accumulate( int [] arr, int sum) { for ( int i : arr) sum += i; return sum; } // Driver Code public static void main(String[] args) { // Test case 1 int [][] graph1 = { { 0 , 1 , 0 , 0 , 1 }, { 1 , 0 , 1 , 1 , 0 }, { 0 , 1 , 0 , 1 , 0 }, { 0 , 1 , 1 , 0 , 0 }, { 1 , 0 , 0 , 0 , 0 } }; int n = graph1.length; findpath(graph1, n); // Test case 2 int [][] graph2 = { { 0 , 1 , 0 , 1 , 1 }, { 1 , 0 , 1 , 0 , 1 }, { 0 , 1 , 0 , 1 , 1 }, { 1 , 1 , 1 , 0 , 0 }, { 1 , 0 , 1 , 0 , 0 } }; n = graph2.length; findpath(graph2, n); // Test case 3 int [][] graph3 = { { 0 , 1 , 0 , 0 , 1 }, { 1 , 0 , 1 , 1 , 1 }, { 0 , 1 , 0 , 1 , 0 }, { 0 , 1 , 1 , 0 , 1 }, { 1 , 1 , 0 , 1 , 0 } }; n = graph3.length; findpath(graph3, n); } } // This code is contributed by // sanjeev2552 |
Python3
# Efficient Python3 program to # find out Eulerian path # Function to find out the path # It takes the adjacency matrix # representation of the graph as input def findpath(graph, n): numofadj = [] # Find out number of edges each # vertex has for i in range (n): numofadj.append( sum (graph[i])) # Find out how many vertex has # odd number edges startpoint, numofodd = 0 , 0 for i in range (n - 1 , - 1 , - 1 ): if (numofadj[i] % 2 = = 1 ): numofodd + = 1 startpoint = i # If number of vertex with odd number of edges # is greater than two return "No Solution". if (numofodd > 2 ): print ( "No Solution" ) return # If there is a path find the path # Initialize empty stack and path # take the starting current as discussed stack = [] path = [] cur = startpoint # Loop will run until there is element in the # stack or current edge has some neighbour. while ( len (stack) > 0 or sum (graph[cur])! = 0 ): # If current node has not any neighbour # add it to path and pop stack set new # current to the popped element if ( sum (graph[cur]) = = 0 ): path.append(cur) cur = stack[ - 1 ] del stack[ - 1 ] # If the current vertex has at least one # neighbour add the current vertex to stack, # remove the edge between them and set the # current to its neighbour. else : for i in range (n): if (graph[cur][i] = = 1 ): stack.append(cur) graph[cur][i] = 0 graph[i][cur] = 0 cur = i break # Print the path for ele in path: print (ele, end = " -> " ) print (cur) # Driver Code if __name__ = = '__main__' : # Test case 1 graph1 = [ [ 0 , 1 , 0 , 0 , 1 ], [ 1 , 0 , 1 , 1 , 0 ], [ 0 , 1 , 0 , 1 , 0 ], [ 0 , 1 , 1 , 0 , 0 ], [ 1 , 0 , 0 , 0 , 0 ] ] n = len (graph1) findpath(graph1, n) # Test case 2 graph2 = [ [ 0 , 1 , 0 , 1 , 1 ], [ 1 , 0 , 1 , 0 , 1 ], [ 0 , 1 , 0 , 1 , 1 ], [ 1 , 1 , 1 , 0 , 0 ], [ 1 , 0 , 1 , 0 , 0 ] ] n = len (graph2) findpath(graph2, n) # Test case 3 graph3 = [ [ 0 , 1 , 0 , 0 , 1 ], [ 1 , 0 , 1 , 1 , 1 ], [ 0 , 1 , 0 , 1 , 0 ], [ 0 , 1 , 1 , 0 , 1 ], [ 1 , 1 , 0 , 1 , 0 ] ] n = len (graph3) findpath(graph3, n) # This code is contributed by mohit kumar 29 |
C#
// Efficient C# program to // find out Eulerian path using System; using System.Collections.Generic; class GFG{ // Function to find out the path // It takes the adjacency matrix // representation of the graph // as input static void findpath( int [,] graph, int n) { List< int > numofadj = new List< int >(); // Find out number of edges // each vertex has for ( int i = 0; i < n; i++) numofadj.Add(accumulate(graph, i, 0)); // Find out how many vertex has // odd number edges int startPoint = 0, numofodd = 0; for ( int i = n - 1; i >= 0; i--) { if (numofadj[i] % 2 == 1) { numofodd++; startPoint = i; } } // If number of vertex with odd // number of edges is greater than // two return "No Solution". if (numofodd > 2) { Console.WriteLine( "No Solution" ); return ; } // If there is a path find the path // Initialize empty stack and path // take the starting current as // discussed Stack< int > stack = new Stack< int >(); List< int > path = new List< int >(); int cur = startPoint; // Loop will run until there is element // in the stack or current edge has some // neighbour. while (stack.Count != 0 || accumulate(graph, cur, 0) != 0) { // If current node has not any // neighbour add it to path and // pop stack set new current to // the popped element if (accumulate(graph,cur, 0) == 0) { path.Add(cur); cur = stack.Pop(); // If the current vertex has at // least one neighbour add the // current vertex to stack, remove // the edge between them and set the // current to its neighbour. } else { for ( int i = 0; i < n; i++) { if (graph[cur, i] == 1) { stack.Push(cur); graph[cur, i] = 0; graph[i, cur] = 0; cur = i; break ; } } } } // print the path foreach ( int ele in path) Console.Write(ele + " -> " ); Console.WriteLine(cur); } static int accumulate( int [,] matrix, int row, int sum) { int []arr = GetRow(matrix, row); foreach ( int i in arr) sum += i; return sum; } public static int [] GetRow( int [,] matrix, int row) { var rowLength = matrix.GetLength(1); var rowVector = new int [rowLength]; for ( var i = 0; i < rowLength; i++) rowVector[i] = matrix[row, i]; return rowVector; } // Driver Code public static void Main(String[] args) { // Test case 1 int [,] graph1 = {{0, 1, 0, 0, 1}, {1, 0, 1, 1, 0}, {0, 1, 0, 1, 0}, {0, 1, 1, 0, 0}, {1, 0, 0, 0, 0}}; int n = graph1.GetLength(0); findpath(graph1, n); // Test case 2 int [,] graph2 = {{0, 1, 0, 1, 1}, {1, 0, 1, 0, 1}, {0, 1, 0, 1, 1}, {1, 1, 1, 0, 0}, {1, 0, 1, 0, 0}}; n = graph2.GetLength(0); findpath(graph2, n); // Test case 3 int [,] graph3 = {{0, 1, 0, 0, 1}, {1, 0, 1, 1, 1}, {0, 1, 0, 1, 0}, {0, 1, 1, 0, 1}, {1, 1, 0, 1, 0}}; n = graph3.GetLength(0); findpath(graph3, n); } } // This code is contributed by Rajput-Ji |
输出:
4 -> 0 -> 1 -> 3 -> 2 -> 1 No Solution 4 -> 3 -> 2 -> 1 -> 4 -> 0 -> 1 -> 3
时间复杂性: 该算法的运行时复杂度为O(E)。该算法也可用于求解欧拉回路。如果路径的第一个顶点和最后一个顶点相同,那么它将是一个欧拉回路。
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



