数学|欧拉和哈密顿路径

先决条件—— 图论基础 某些图问题涉及在两个顶点之间找到一条路径，使每条边只经过一次，或者在访问时在两个顶点之间找到一条路径 每个顶点 就一次。这些路径被称为 欧拉路径 和 哈密顿路径 分别地

欧拉路径问题最早是在17世纪提出的。

欧拉路径和回路：

• Euler路径是使用图的每条边的路径 就一次 .
• Euler回路是一个只使用图的每条边一次的回路。
• Euler路径从不同的顶点开始和结束。
• Euler回路在同一顶点开始和结束。

这个 科尼斯伯格桥 问题的图形表示：

有简单的标准来确定多重图是有欧拉路径还是欧拉回路。对于任何多重图，要有一个欧拉回路，顶点的所有度数都必须是偶数。

定理—— “至少有两个顶点的连通多重图（和简单图）有一个Euler回路当且仅当 每个 它的顶点有一个 均匀度 .”

证明上述说法的证据是，每次电路通过一个顶点时，它都会增加两次次数。因为它是一个回路，它在同一个顶点开始和结束，这使得它在回路开始时贡献一度，在回路结束时贡献一度。这样，每个顶点都有一个偶数度。 由于konigsberg图的顶点具有奇数度，因此图中不存在Euler回路。

定理—— “连通多重图（和简单图）有一条Euler路径，但没有Euler回路，当且仅当它有 正好有两个顶点 “奇怪的程度。”

该证明是上述证明的扩展。由于路径的起点和终点可能不同，因此允许路径起点和终点的顶点具有奇数度。

• 例如—— 下面显示的哪些图形具有Euler路径或Euler回路？

• 解决方案—— 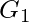有两个奇数度的顶点 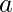和 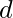其余的人都有相同的学位。所以这个图有一条欧拉路径，但没有欧拉回路。路径从奇数度的顶点开始和结束。路径是- 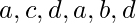. 有四个顶点都是偶数，所以它有一个欧拉回路。电路是—— .

哈密顿路径和电路：

哈密顿路径—— 图中的简单路径 经过 每个顶点正好一次 被称为哈密顿路径。

哈密顿电路—— 图中的简单回路 只经过每个顶点一次的称为哈密顿回路。

与欧拉路径和回路不同，没有简单的必要和充分的条件来确定图中是否存在哈密顿路径或回路。但是，有一些标准排除了图中哈密顿回路的存在，比如——如果图中有一个1度的顶点，那么它就不可能有哈密顿回路。 有一些定理给出了哈密顿图存在的充分条件，但不是必要条件。

狄拉克定理- “如果 是一个带有 顶点与 这样每个顶点在 是 至少 , 然后 有一个哈密顿回路。”

奥雷定理- “如果 是一个带有 顶点与 以至于 对于每对非相邻顶点 和 在里面 然后 有一个哈密顿回路。”

如上所述，上述定理是图中存在哈密顿回路的充分条件，但不是必要条件。有些图有哈密顿回路，但不遵循上述定理中的条件。例如，循环 有一个哈密顿回路，但不遵循这些定理。

注： K _N 是哈密顿电路吗

有许多实际问题可以通过寻找最优哈密顿电路来解决。其中一个问题是旅行推销员问题，它要求通过一组城市的最短路线。

• 例1- 下图是否有哈密顿回路？

• 解决方案- 是的，上图有一个哈密顿回路。解决方案是——

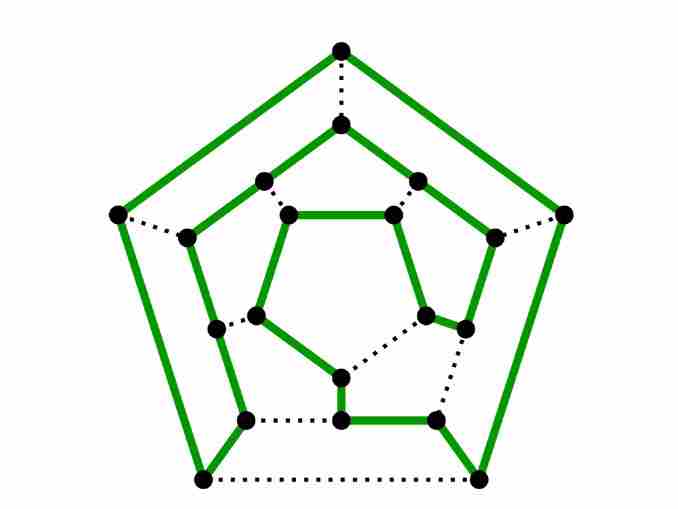
• 例2- 下图是否有哈密顿回路？

• 解决方案- 不，上面的图没有哈密顿回路，因为图中有两个度为1的顶点。

关卡角问题

练习下列问题将有助于测试你的知识。所有问题都是在前几年的GATE或GATE模拟测试中提出的。强烈建议你练习。

1. 2007年CS门，问题23 2. 2005年CS门，问题84 3. CS门2008，问题26

推荐人-

欧拉路径——维基百科 哈密顿路径——维基百科 《离散数学及其应用》，肯尼斯·H·罗森著

本文由 希拉格·曼瓦尼 .如果你喜欢GeekSforgek，并想贡献自己的力量，你也可以使用 写极客。组织 或者把你的文章寄去评论-team@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上，并帮助其他极客。

如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请写下评论。