用弗洛伊德·沃沙尔探测负循环-yiteyi-C++库

我们得到了一个有向图。我们需要计算图是否有负循环。负周期是指周期的总和为负的周期。

null

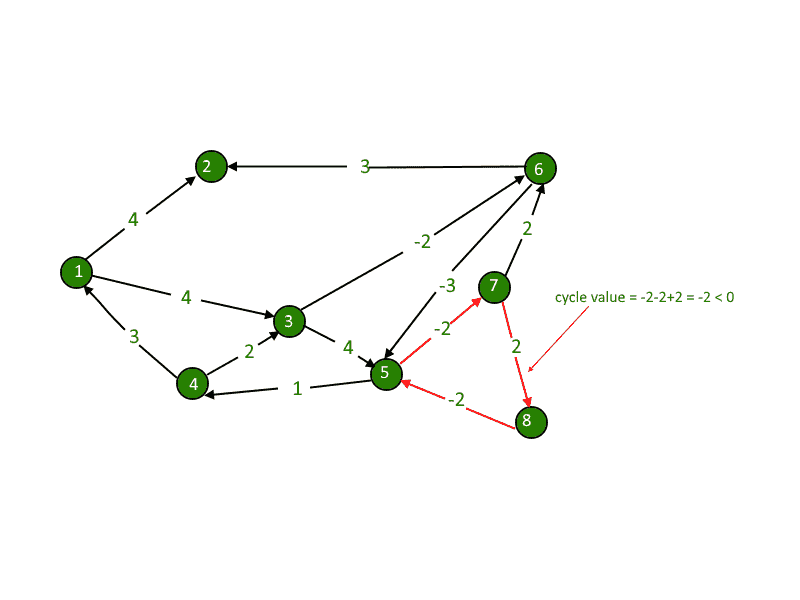
negative_cycle

负权存在于图的各种应用中。例如，如果我们沿着这条路走，我们可能会获得一些优势，而不是为一条路支付成本。例如：

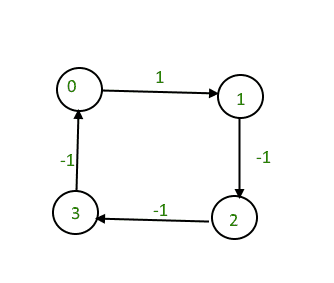
Input : 4 4
        0 1 1
        1 2 -1
        2 3 -1
        3 0 -1

Output : Yes
The graph contains a negative cycle.

Detecting negative cycle using Floyd Warshall

推荐：请尝试你的方法 {IDE} 首先，在进入解决方案之前。

我们讨论过贝尔曼-福特算法基于此问题的解决方案。在这篇帖子里，弗洛伊德·沃沙尔算法讨论了一种既适用于连通图，又适用于非连通图的基解。任何节点与自身的距离始终为零。但在某些情况下，就像在这个例子中，当我们从4到1进一步移动时，距离变成了-2，也就是说，1到1的距离变成了-2。这是我们的目标，我们只需检查节点与自身的距离，如果结果为负，我们将检测所需的负循环。

C++

                         // C++ Program to check if there is a negative weight                       
                         // cycle using Floyd Warshall Algorithm                       
                         #include<bits/stdc++.h>                       
                         using                                     namespace                                     std;                       
                                   
                         // Number of vertices in the graph                       
                         #define V 4                       
                                   
                         /* Define Infinite as a large enough value. This                       
                                                 value will be used for vertices not connected                       
                                                 to each other */                       
                         #define INF 99999                       
                                   
                         // A function to print the solution matrix                       
                         void                                     printSolution(                                     int                                     dist[][V]);                       
                                   
                         // Returns true if graph has negative weight cycle                       
                         // else false.                       
                         bool                                     negCyclefloydWarshall(                                     int                                     graph[][V])                       
                         {                       
                                                 /* dist[][] will be the output matrix that will                       
                                                 finally have the shortest                       
                                                 distances between every pair of vertices */                       
                                                 int                                     dist[V][V], i, j, k;                       
                                   
                                                 /* Initialize the solution matrix same as input                       
                                                 graph matrix. Or we can say the initial values                       
                                                 of shortest distances are based on shortest                       
                                                 paths considering no intermediate vertex. */                       
                                                 for                                     (i = 0; i < V; i++)                       
                                                 for                                     (j = 0; j < V; j++)                       
                                                 dist[i][j] = graph[i][j];                       
                                   
                                                 /* Add all vertices one by one to the set of                       
                                                 intermediate vertices.                       
                                                 ---> Before start of a iteration, we have shortest                       
                                                 distances between all pairs of vertices such                       
                                                 that the shortest distances consider only the                       
                                                 vertices in set {0, 1, 2, .. k-1} as intermediate                       
                                                 vertices.                       
                                                 ----> After the end of a iteration, vertex no. k is                       
                                                 added to the set of intermediate vertices and                       
                                                 the set becomes {0, 1, 2, .. k} */                       
                                                 for                                     (k = 0; k < V; k++)                       
                                                 {                       
                                                 // Pick all vertices as source one by one                       
                                                 for                                     (i = 0; i < V; i++)                       
                                                 {                       
                                                 // Pick all vertices as destination for the                       
                                                 // above picked source                       
                                                 for                                     (j = 0; j < V; j++)                       
                                                 {                       
                                                 // If vertex k is on the shortest path from                       
                                                 // i to j, then update the value of dist[i][j]                       
                                                 if                                     (dist[i][k] + dist[k][j] < dist[i][j])                       
                                                 dist[i][j] = dist[i][k] + dist[k][j];                       
                                                 }                       
                                                 }                       
                                                 }                       
                                   
                                                 // If distance of any vertex from itself                       
                                                 // becomes negative, then there is a negative                       
                                                 // weight cycle.                       
                                                 for                                     (                                     int                                     i = 0; i < V; i++)                       
                                                 if                                     (dist[i][i] < 0)                       
                                                 return                                     true                                     ;                       
                                                 return                                     false                                     ;                       
                         }                       
                                   
                                                 // driver program                       
                         int                                     main()                       
                         {                       
                                                 /* Let us create the following weighted graph                       
                                                 1                       
                                                 (0)----------->(1)                       
                                                 /|             |                       
                                                 |              |                       
                                                 -1 |              | -1                       
                                                 |             |/                       
                                                 (3)<-----------(2)                       
                                                 -1       */                       
                                   
                                                 int                                     graph[V][V] = { {0   , 1   , INF , INF},                       
                                                 {INF , 0   , -1  , INF},                       
                                                 {INF , INF , 0   ,  -1},                       
                                                 {-1  , INF , INF ,   0}};                       
                                   
                                                 if                                     (negCyclefloydWarshall(graph))                       
                                                 cout <<                                     "Yes"                                     ;                       
                                                 else                       
                                                 cout <<                                     "No"                                     ;                       
                                                 return                                     0;                       
                         }                       

JAVA

                         // Java Program to check if there is a negative weight                       
                         // cycle using Floyd Warshall Algorithm                       
                         class                                     GFG                       
                         {                       
                                   
                                                 // Number of vertices in the graph                       
                                                 static                                     final                                     int                                     V =                                     4                                     ;                       
                                   
                                                 /* Define Infinite as a large enough value. This                       
                                                 value will be used for vertices not connected                       
                                                 to each other */                       
                                                 static                                     final                                     int                                     INF =                                     99999                                     ;                       
                                   
                                                 // Returns true if graph has negative weight cycle                       
                                                 // else false.                       
                                                 static                                     boolean                                     negCyclefloydWarshall(                                     int                                     graph[][])                       
                                                 {                       
                                   
                                                 /* dist[][] will be the output matrix that will                       
                                                 finally have the shortest                       
                                                 distances between every pair of vertices */                       
                                                 int                                     dist[][] =                                     new                                     int                                     [V][V], i, j, k;                       
                                   
                                                 /* Initialize the solution matrix same as input                       
                                                 graph matrix. Or we can say the initial values                       
                                                 of shortest distances are based on shortest                       
                                                 paths considering no intermediate vertex. */                       
                                                 for                                     (i =                                     0                                     ; i < V; i++)                       
                                                 for                                     (j =                                     0                                     ; j < V; j++)                       
                                                 dist[i][j] = graph[i][j];                       
                                   
                                                 /* Add all vertices one by one to the set of                       
                                                 intermediate vertices.                       
                                                 ---> Before start of a iteration, we have shortest                       
                                                 distances between all pairs of vertices such                       
                                                 that the shortest distances consider only the                       
                                                 vertices in set {0, 1, 2, .. k-1} as intermediate                       
                                                 vertices.                       
                                                 ----> After the end of a iteration, vertex no. k is                       
                                                 added to the set of intermediate vertices and                       
                                                 the set becomes {0, 1, 2, .. k} */                       
                                                 for                                     (k =                                     0                                     ; k < V; k++)                       
                                                 {                       
                                   
                                                 // Pick all vertices as source one by one                       
                                                 for                                     (i =                                     0                                     ; i < V; i++)                       
                                                 {                       
                                   
                                                 // Pick all vertices as destination for the                       
                                                 // above picked source                       
                                                 for                                     (j =                                     0                                     ; j < V; j++)                       
                                                 {                       
                                   
                                                 // If vertex k is on the shortest path from                       
                                                 // i to j, then update the value of dist[i][j]                       
                                                 if                                     (dist[i][k] + dist[k][j] < dist[i][j])                       
                                                 dist[i][j] = dist[i][k] + dist[k][j];                       
                                                 }                       
                                                 }                       
                                                 }                       
                                   
                                                 // If distance of any vertex from itself                       
                                                 // becomes negative, then there is a negative                       
                                                 // weight cycle.                       
                                                 for                                     (i =                                     0                                     ; i < V; i++)                       
                                                 if                                     (dist[i][i] <                                     0                                     )                       
                                                 return                                     true                                     ;                       
                                   
                                                 return                                     false                                     ;                       
                                                 }                       
                                   
                                                 // Driver code                       
                                                 public                                     static                                     void                                     main (String[] args)                       
                                                 {                       
                                   
                                                 /* Let us create the following weighted graph                       
                                                 1                       
                                                 (0)----------->(1)                       
                                                 /|               |                       
                                                 |               |                       
                                                 -1 |               | -1                       
                                                 |                |/                       
                                                 (3)<-----------(2)                       
                                                 -1     */                       
                                   
                                                 int                                     graph[][] = { {                                     0                                     ,                                     1                                     , INF, INF},                       
                                                 {INF,                                     0                                     , -                                     1                                     , INF},                       
                                                 {INF, INF,                                     0                                     , -                                     1                                     },                       
                                                 {-                                     1                                     , INF, INF,                                     0                                     }};                       
                                   
                                                 if                                     (negCyclefloydWarshall(graph))                       
                                                 System.out.print(                                     "Yes"                                     );                       
                                                 else                       
                                                 System.out.print(                                     "No"                                     );                       
                                                 }                       
                         }                       
                                   
                         // This code is contributed by Anant Agarwal.                       

Python3

                         # Python Program to check                       
                         # if there is a                       
                         # negative weight                       
                         # cycle using Floyd                       
                         # Warshall Algorithm                       
                                   
                                   
                         # Number of vertices                       
                         # in the graph                       
                         V                                     =                                     4                       
                                   
                         # Define Infinite as a                       
                         # large enough value. This                       
                         # value will be used                       
                         #for vertices not connected                       
                         # to each other                       
                         INF                                     =                                     99999                       
                                   
                         # Returns true if graph has                       
                         # negative weight cycle                       
                         # else false.                       
                         def                                     negCyclefloydWarshall(graph):                       
                                   
                                                 # dist[][] will be the                       
                                                 # output matrix that will                       
                                                 # finally have the shortest                       
                                                 # distances between every                       
                                                 # pair of vertices                       
                                                 dist                                     =                                     [[                                     0                                     for                                     i                                     in                                     range                                     (V                                     +                                     1                                     )]                                     for                                     j                                     in                                     range                                     (V                                     +                                     1                                     )]                       
                                   
                                                 # Initialize the solution                       
                                                 # matrix same as input                       
                                                 # graph matrix. Or we can                       
                                                 # say the initial values                       
                                                 # of shortest distances                       
                                                 # are based on shortest                       
                                                 # paths considering no                       
                                                 # intermediate vertex.                       
                                                 for                                     i                                     in                                     range                                     (V):                       
                                                 for                                     j                                     in                                     range                                     (V):                       
                                                 dist[i][j]                                     =                                     graph[i][j]                       
                                   
                                                 ''' Add all vertices one                       
                                                 by one to the set of                       
                                                 intermediate vertices.                       
                                                 ---> Before start of a iteration,                       
                                                 we have shortest                       
                                                 distances between all pairs                       
                                                 of vertices such                       
                                                 that the shortest distances                       
                                                 consider only the                       
                                                 vertices in set {0, 1, 2, .. k-1}                       
                                                 as intermediate vertices.                       
                                                 ----> After the end of a iteration,                       
                                                 vertex no. k is                       
                                                 added to the set of                       
                                                 intermediate vertices and                       
                                                 the set becomes {0, 1, 2, .. k} '''                       
                                                 for                                     k                                     in                                     range                                     (V):                       
                                   
                                                 # Pick all vertices                       
                                                 # as source one by one                       
                                                 for                                     i                                     in                                     range                                     (V):                       
                                   
                                                 # Pick all vertices as                       
                                                 # destination for the                       
                                                 # above picked source                       
                                                 for                                     j                                     in                                     range                                     (V):                       
                                   
                                                 # If vertex k is on                       
                                                 # the shortest path from                       
                                                 # i to j, then update                       
                                                 # the value of dist[i][j]                       
                                                 if                                     (dist[i][k]                                     +                                     dist[k][j] < dist[i][j]):                       
                                                 dist[i][j]                                     =                                     dist[i][k]                                     +                                     dist[k][j]                       
                                   
                                                 # If distance of any                       
                                                 # vertex from itself                       
                                                 # becomes negative, then                       
                                                 # there is a negative                       
                                                 # weight cycle.                       
                                                 for                                     i                                     in                                     range                                     (V):                       
                                                 if                                     (dist[i][i] <                                     0                                     ):                       
                                                 return                                     True                       
                                   
                                                 return                                     False                       
                                   
                                   
                         # Driver code                       
                                   
                                   
                         ''' Let us create the                       
                                                 following weighted graph                       
                                                 1                       
                                                 (0)----------->(1)                       
                                                 /|               |                       
                                                 |               |                       
                                                 -1 |               | -1                       
                                                 |                |/                       
                                                 (3)<-----------(2)                       
                                                 -1     '''                       
                                   
                         graph                                     =                                     [ [                                     0                                     ,                                     1                                     , INF, INF],                       
                                                 [INF,                                     0                                     ,                                     -                                     1                                     , INF],                       
                                                 [INF, INF,                                     0                                     ,                                     -                                     1                                     ],                       
                                                 [                                     -                                     1                                     , INF, INF,                                     0                                     ]]                       
                                   
                         if                                     (negCyclefloydWarshall(graph)):                       
                                                 print                                     (                                     "Yes"                                     )                       
                         else                                     :                       
                                                 print                                     (                                     "No"                                     )                       
                                   
                         # This code is contributed                       
                         # by Anant Agarwal.                       

C#

                         // C# Program to check if there                       
                         // is a negative weight cycle                       
                         // using Floyd Warshall Algorithm                       
                                   
                         using                                     System;                       
                                   
                         namespace                                     Cycle                       
                         {                       
                         public                                     class                                     GFG                       
                         {                       
                                   
                                   
                                                 // Number of vertices in the graph                       
                                                 static                                     int                                     V = 4;                       
                                   
                                                 /* Define Infinite as a large enough value. This                       
                                                 value will be used for vertices not connected                       
                                                 to each other */                       
                                                 static                                     int                                     INF = 99999;                       
                                   
                                                 // Returns true if graph has negative weight cycle                       
                                                 // else false.                       
                                                 static                                     bool                                     negCyclefloydWarshall(                                     int                                     [,]graph)                       
                                                 {                       
                                   
                                                 /* dist[][] will be the output matrix that will                       
                                                 finally have the shortest                       
                                                 distances between every pair of vertices */                       
                                                 int                                     [,]dist =                                     new                                     int                                     [V,V];                       
                                                 int                                     i, j, k;                       
                                   
                                                 /* Initialize the solution matrix same as input                       
                                                 graph matrix. Or we can say the initial values                       
                                                 of shortest distances are based on shortest                       
                                                 paths considering no intermediate vertex. */                       
                                                 for                                     (i = 0; i < V; i++)                       
                                                 for                                     (j = 0; j < V; j++)                       
                                                 dist[i,j] = graph[i,j];                       
                                   
                                                 /* Add all vertices one by one to the set of                       
                                                 intermediate vertices.                       
                                                 ---> Before start of a iteration, we have shortest                       
                                                 distances between all pairs of vertices such                       
                                                 that the shortest distances consider only the                       
                                                 vertices in set {0, 1, 2, .. k-1} as intermediate                       
                                                 vertices.                       
                                                 ----> After the end of a iteration, vertex no. k is                       
                                                 added to the set of intermediate vertices and                       
                                                 the set becomes {0, 1, 2, .. k} */                       
                                                 for                                     (k = 0; k < V; k++)                       
                                                 {                       
                                   
                                                 // Pick all vertices as source one by one                       
                                                 for                                     (i = 0; i < V; i++)                       
                                                 {                       
                                   
                                                 // Pick all vertices as destination for the                       
                                                 // above picked source                       
                                                 for                                     (j = 0; j < V; j++)                       
                                                 {                       
                                   
                                                 // If vertex k is on the shortest path from                       
                                                 // i to j, then update the value of dist[i][j]                       
                                                 if                                     (dist[i,k] + dist[k,j] < dist[i,j])                       
                                                 dist[i,j] = dist[i,k] + dist[k,j];                       
                                                 }                       
                                                 }                       
                                                 }                       
                                   
                                                 // If distance of any vertex from itself                       
                                                 // becomes negative, then there is a negative                       
                                                 // weight cycle.                       
                                                 for                                     (i = 0; i < V; i++)                       
                                                 if                                     (dist[i,i] < 0)                       
                                                 return                                     true                                     ;                       
                                   
                                                 return                                     false                                     ;                       
                                                 }                       
                                   
                                                 // Driver code                       
                                                 public                                     static                                     void                                     Main()                       
                                                 {                       
                                   
                                                 /* Let us create the following weighted graph                       
                                                 1                       
                                                 (0)----------->(1)                       
                                                 /|             |                       
                                                 |             |                       
                                                 -1 |             | -1                       
                                                 |             |/                       
                                                 (3)<-----------(2)                       
                                                 -1     */                       
                                   
                                                 int                                     [,]graph = { {0, 1, INF, INF},                       
                                                 {INF, 0, -1, INF},                       
                                                 {INF, INF, 0, -1},                       
                                                 {-1, INF, INF, 0}};                       
                                   
                                                 if                                     (negCyclefloydWarshall(graph))                       
                                                 Console.Write(                                     "Yes"                                     );                       
                                                 else                       
                                                 Console.Write(                                     "No"                                     );                       
                                                 }                       
                         }                       
                         }                       
                                   
                         // This code is contributed by Sam007.                       

Javascript

                         <script>                       
                                   
                         // JavaScript Program to check if there                       
                         // is a negative weight cycle                       
                         // using Floyd Warshall Algorithm                       
                         // Number of vertices in the graph                       
                         var                                     V = 4;                       
                                   
                         /* Define Infinite as a large enough value. This                       
                         value will be used for vertices not connected                       
                         to each other */                       
                         var                                     INF = 99999;                       
                                   
                         // Returns true if graph has negative weight cycle                       
                         // else false.                       
                         function                                     negCyclefloydWarshall(graph)                       
                         {                       
                                   
                                                 /* dist[][] will be the output matrix that will                       
                                                 finally have the shortest                       
                                                 distances between every pair of vertices */                       
                                                 var                                     dist = Array.from(Array(V), ()=>Array(V));                       
                                                 var                                     i, j, k;                       
                                   
                                                 /* Initialize the solution matrix same as input                       
                                                 graph matrix. Or we can say the initial values                       
                                                 of shortest distances are based on shortest                       
                                                 paths considering no intermediate vertex. */                       
                                                 for                                     (i = 0; i < V; i++)                       
                                                 for                                     (j = 0; j < V; j++)                       
                                                 dist[i][j] = graph[i][j];                       
                                   
                                                 /* Add all vertices one by one to the set of                       
                                                 intermediate vertices.                       
                                                 ---> Before start of a iteration, we have shortest                       
                                                 distances between all pairs of vertices such                       
                                                 that the shortest distances consider only the                       
                                                 vertices in set {0, 1, 2, .. k-1} as intermediate                       
                                                 vertices.                       
                                                 ----> After the end of a iteration, vertex no. k is                       
                                                 added to the set of intermediate vertices and                       
                                                 the set becomes {0, 1, 2, .. k} */                       
                                                 for                                     (k = 0; k < V; k++)                       
                                                 {                       
                                   
                                                 // Pick all vertices as source one by one                       
                                                 for                                     (i = 0; i < V; i++)                       
                                                 {                       
                                   
                                                 // Pick all vertices as destination for the                       
                                                 // above picked source                       
                                                 for                                     (j = 0; j < V; j++)                       
                                                 {                       
                                   
                                                 // If vertex k is on the shortest path from                       
                                                 // i to j, then update the value of dist[i][j]                       
                                                 if                                     (dist[i][k] + dist[k][j] < dist[i][j])                       
                                                 dist[i][j] = dist[i][k] + dist[k][j];                       
                                                 }                       
                                                 }                       
                                                 }                       
                                   
                                                 // If distance of any vertex from itself                       
                                                 // becomes negative, then there is a negative                       
                                                 // weight cycle.                       
                                                 for                                     (i = 0; i < V; i++)                       
                                                 if                                     (dist[i][i] < 0)                       
                                                 return                                     true                                     ;                       
                                                 return                                     false                                     ;                       
                         }                       
                                   
                         // Driver code                       
                                   
                         /* Let us create the following weighted graph                       
                                                 1                       
                                                 (0)----------->(1)                       
                                                 /|             |                       
                                                 |             |                       
                         -1 |             | -1                       
                                                 |             |/                       
                                                 (3)<-----------(2)                       
                                                 -1     */                       
                                   
                         var                                     graph = [ [0, 1, INF, INF],                       
                                                 [INF, 0, -1, INF],                       
                                                 [INF, INF, 0, -1],                       
                                                 [-1, INF, INF, 0]];                       
                                   
                         if                                     (negCyclefloydWarshall(graph))                       
                                                 document.write(                                     "Yes"                                     );                       
                         else                       
                                                 document.write(                                     "No"                                     );                       
                                   
                                   
                         </script>                       

输出：

Yes

本文由 希瓦尼·米塔尔 .如果你喜欢GeekSforgek，并想贡献自己的力量，你也可以使用写极客。组织或者把你的文章寄去评论-team@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上，并帮助其他极客。如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请写下评论。

文章版权归作者所有，未经允许请勿转载。

THE END

技术文章