使用Bresenham算法的圆上点的邻域-yiteyi-C++库

给定圆心及其半径。我们的任务是找到离散圆上任意点的邻域。例如：

null

Input :  Center = (0, 0),          Radius = 3          Point for determining neighbors = (2, 2)Output : Neighbors of given point are : (1, 3), (3, 1)Input : Center = (2, 2)         Radius 2        Point of determining neighbors = (0, 2)Output : Neighbors of given point are : (1, 4), (3, 4)

离散圆上任何点的邻域都是从其原始x坐标中减去一个或多个x坐标的点。

推荐：请尝试你的方法 {IDE} 首先，在进入解决方案之前。

我们使用 bresenham圆生成算法提取出在计算机屏幕上画一个像素圆所需的整数点。

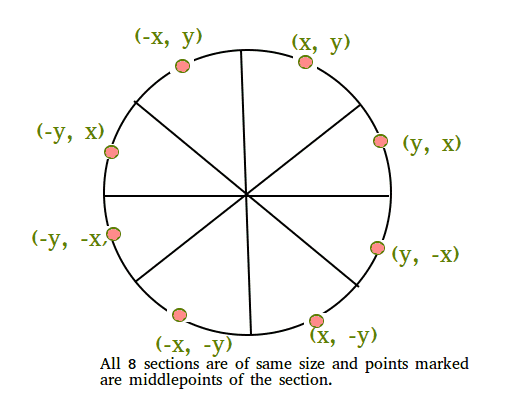
Breshanham

圆具有高度对称的特性，这是在计算机像素屏幕上绘制圆所必需的。Bresenham的圆算法计算前45度内像素的位置，并使用圆的8向对称特性计算以原点为中心的圆外围的剩余像素。

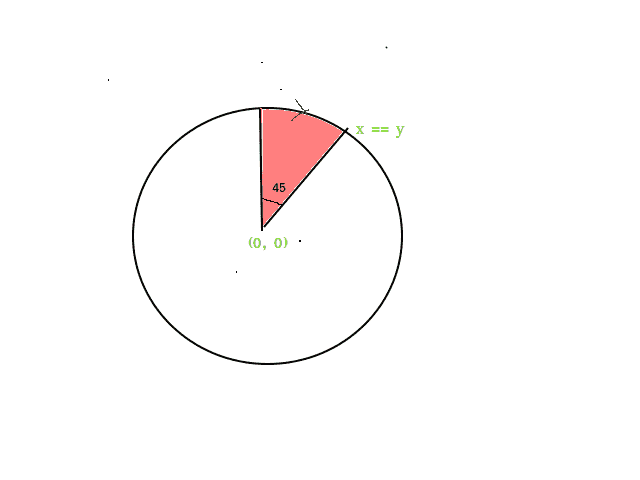
Breshanham2

求导：考虑一个无穷小的连续圆弧，如下图所示，假设我们要沿中心的原点顺时针圆弧运动，半径R和我们的运动位于第一个八角体中，在第一个八分体上，所以我们的极限是（0，r）到（r／）。 $sqrt{2}$ ，r/ $sqrt{2}$ )其中x=y。正如我们所知，在这个特定的八分之一点中，y坐标的减少小于x坐标的增加，或者你可以说，沿x轴的运动大于沿y轴的运动，所以，x坐标总是在第一个八分之一点增加。现在，我们想知道y是否会随x变化。为了知道y随x的变化，bresenham引入了一个名为decision parameter的变量，该变量将在循环运行时更新其值。现在，我们需要了解，我们将如何选择下一个像素，在图中，f（N）和f（S）分别是计算从原点到像素N和S的距离所涉及的误差，取较小值，我们将选择该像素。判定参数定义为d=f（N）+f（S），如果d<=0，则N将是下一个像素，否则S将是下一个像素。我们将继续这样做，直到x 本文主要关注的不是bresenham的算法，因此，我将跳过决策参数的推导，但如果您想了解决策参数的推导，请转到参考链接。注：一个点的邻域可以是任意数量的，并且邻域的y坐标应该与其输入像素具有相同的符号，对于y坐标为零的像素，我们将打印出所有的邻域，而不管其符号如何。离散几何对象由一组有限的整数点组成。这一组通常非常稀疏。因此，数组表示法在存储时根本不节省空间。我们将使用哈希映射，数据值是y坐标和键值作为x坐标的链表。我们可以使用键值轻松访问它们，这也是一种节省空间的方法。下面是用于确定给定点的邻居的C++ STL程序。

CPP

                         // C++ program to find neighbors of a given point on circle                       
                         #include <bits/stdc++.h>                       
                         using                                     namespace                                     std;                       
           
                         // map to store all the pixels of circle                       
                         map<                                     int                                     , list<                                     int                                     > > mymap;                       
                         map<                                     int                                     , list<                                     int                                     > >::iterator it;                       
           
                         // This program will print all the stored pixels.                       
                         void                                     showallpoints(map<                                     int                                     , list<                                     int                                     > >& mymap)                       
                         {                       
                                                 // To print out all the stored pixels,                       
                                                 // we will traverse the map using iterator                       
                                                 for                                     (it = mymap.begin(); it != mymap.end(); it++) {                       
           
                                                 // List contains all the y-coordinate.                       
                                                 list<                                     int                                     > temp = it->second;                       
           
                                                 for                                     (                                     auto                                     p = temp.begin(); p != temp.end(); p++) {                       
                                                 cout <<                                     "("                                     << it->first <<                                     ", "                                     << *p <<                                     ")"                                     ;                       
                                                 }                       
                                                 }                       
                         }                       
           
                         // This function will stored the pixels.                       
                         void                                     putpixelone(                                     int                                     m,                                     int                                     n, map<                                     int                                     , list<                                     int                                     > >& mymap)                       
                         {                       
                                                 // check if the given pixel is present already in the                       
                                                 // map then discard that pixel and return the function.                       
                                                 map<                                     int                                     , list<                                     int                                     > >::iterator it;                       
           
                                                 // if x-coordinate of the pixel is present in the map then                       
                                                 // it will give iterator pointing to list of those pixels                       
                                                 // which are having same x-coordinate as the input pixel                       
                                                 if                                     (mymap.find(m) != mymap.end()) {                       
           
                                                 it = mymap.find(m);                       
                                                 list<                                     int                                     > temp = it->second;                       
                                                 list<                                     int                                     >::iterator p;                       
           
                                                 // Checking for y coordinate                       
                                                 for                                     (p = temp.begin(); p != temp.end(); p++)                       
                                                 if                                     (*p == n)                       
                                                 return                                     ;                       
           
                                                 // if map doesn't contain pixels having same y-                       
                                                 // coordinate then pixel are different and store                       
                                                 // the pixel                       
                                                 mymap[m].push_back(n);                       
                                                 }                                     else                       
           
                                                 // Neither x nor y coordinate are same.                       
                                                 // put the pixel into the map                       
                                                 mymap[m].push_back(n);                       
           
                                                 return                                     ;                       
                         }                       
           
                         // generate all the pixels using 8 way-symmetry of circle                       
                         void                                     putpixelall(                                     int                                     p,                                     int                                     q,                                     int                                     x1,                                     int                                     y1)                       
                         {                       
                                                 putpixelone(p + x1, q + y1, mymap);                       
                                                 putpixelone(q + x1, p + y1, mymap);                       
                                                 putpixelone(q + x1, -p + y1, mymap);                       
                                                 putpixelone(p + x1, -q + y1, mymap);                       
                                                 putpixelone(-p + x1, -q + y1, mymap);                       
                                                 putpixelone(-q + x1, -p + y1, mymap);                       
                                                 putpixelone(-q + x1, p + y1, mymap);                       
                                                 putpixelone(-p + x1, q + y1, mymap);                       
                                                 return                                     ;                       
                         }                       
           
                         // Brensenham's circle algorithm                       
                         void                                     circle(                                     int                                     centerx,                                     int                                     centery,                                     int                                     r)                       
                         {                       
                                                 // initial coordinate will be (0, radius) and we                       
                                                 // will move counter-clockwise from this coordinate                       
                                                 int                                     x = 0;                       
                                                 int                                     y = r;                       
           
                                                 // decision parameter for initial coordinate                       
                                                 float                                     decision_para = 3 - 2 * (r);                       
                                                 putpixelall(x, y, centerx, centery);                       
           
                                                 while                                     (x < y) {                       
           
                                                 // x will always increase by 1 unit                       
                                                 x = x + 1;                       
                                                 if                                     (decision_para <= 0) {                       
           
                                                 // if decision parameter is negative then N                       
                                                 // will be next pixel N(x+1, y)                       
                                                 decision_para = decision_para + 4 * x + 6;                       
                                                 }                                     else                                     {                       
           
                                                 // if decision parameter is positive then N                       
                                                 // will be next pixel S(x+1, y-1)                       
                                                 y = y - 1;                       
                                                 decision_para = decision_para + 4 * (x - y) + 10;                       
                                                 }                       
           
                                                 // Function call to generate all the pixels by symmetry                       
                                                 putpixelall(x, y, centerx, centery);                       
                                                 }                       
                                                 return                                     ;                       
                         }                       
                         // this program will find the neighbors of a given point`                       
                         void                                     neighbours(map<                                     int                                     , list<                                     int                                     > >& mymap,                                     int                                     given_pointx,                       
                                                 int                                     given_pointy)                       
                         {                       
                                                 for                                     (it = mymap.begin(); it != mymap.end(); ++it) {                       
                                                 if                                     (it->first == given_pointx + 1 ||                       
                                                 it->first == given_pointx - 1) {                       
                                                 list<                                     int                                     > temp1 = it->second;                       
                                                 list<                                     int                                     >::iterator itr1;                       
                                                 for                                     (itr1 = temp1.begin(); itr1 != temp1.end(); ++itr1) {                       
           
                                                 // Checking for same-sign.                       
                                                 if                                     (given_pointy >= 0 && *itr1 >= 0)                       
                                                 cout <<                                     "("                                     << it->first <<                                     ", "                                     << *itr1 <<                                     ")"                                     ;                       
                                                 else                                     if                                     (given_pointy <= 0 && *itr1 <= 0)                       
                                                 cout <<                                     "("                                     << it->first <<                                     ", "                                     << *itr1 <<                                     ")"                                     ;                       
                                                 else                       
                                                 continue                                     ;                       
                                                 }                       
                                                 }                       
                                                 }                       
                         }                       
           
                         // Driver code                       
                         int                                     main()                       
                         {                       
                                                 int                                     center_x = 0, center_y = 0;                       
                                                 float                                     r = 3.0;                       
                                                 circle(center_x, center_y, r);                       
                                                 showallpoints(mymap);                       
                                                 int                                     nx = 3, ny = 0;                       
                                                 neighbours(mymap, nx, ny);                       
                                                 cout << endl;                       
                                                 return                                     0;                       
                         }                       

输出：

(-3, 0), (-3, -1), (-3, 1), (-2, -2), (-2, 2), (-1, -3), (-1, 3), (0, 3)(0, -3), (1, 3), (1, -3), (2, 2), (2, -2), (3, 0), (3, 1), (3, -1) Neighbours of given point are : (2, 2), (2, -2)

参考资料： https://www.slideshare.net/tahersb/bresenham-circle 本文由 刺耳的库马尔·辛格 .如果你喜欢GeekSforgek，并想贡献自己的力量，你也可以使用写极客。组织或者把你的文章寄去评论-team@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上，并帮助其他极客。如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请写下评论。

文章版权归作者所有，未经允许请勿转载。

THE END

技术文章