给定三个整数a、b和m。找到一个整数 K 以至于 
其中a和m是相对素数。如果任何k都不可能满足这个关系，请打印-1。 例如：
null
Input: 2 3 5Output: 3Explanation:a = 2, b = 3, m = 5The value which satisfies the above equationis 3, because => 23 = 2 * 2 * 2 = 8=> 23 (mod 5) = 8 (mod 5) => 3which is equal to b i.e., 3.Input: 3 7 11Output: -1
A. 天真的方法 就是从0到m运行一个循环，覆盖k的所有可能值，并检查满足上述关系的k值。如果k的所有值都已用尽，则打印-1。该方法的时间复杂度为O（m） 一 有效率的 方法是使用 小步，大步算法 通过使用 中招 .
小步巨步算法
给定一个阶为’m’的循环群G，一个群的生成器’a’和一个群元素’b’，问题是找到一个整数’k’，使得 所以我们要做的是（根据中间技巧），把问题分成两部分。 
然后逐个求解，然后找到碰撞。
Now according to the baby-step giant-step algorithm, we can write 'k' aswith
and
and
.Therefore, we have:
Therefore in order to solve, we precompute
for different values of 'i'. Then fix 'b' and tries values of 'j' In RHS of the congruence relation above. It tests to see if congruence is satisfied for any value of 'j', using precomputed values of LHS.
让我们看看如何使用上述算法解决我们的问题：- 首先，我们必须写作 
哪里 
显然，任何价值 K 中间休息时 [0，m） 可以用这种形式表示，其中 
和 
将上述等式中的“k”替换为：- 
- 术语left和right只能取n个不同的值作为
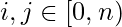因此，我们需要为等式的左或右部分生成所有这些术语，并将它们存储在数组或数据结构中，如C/C++中的map/unordered_map或java中的Hashmap。 - 假设我们已经存储了LHS的所有值。现在迭代RHS上不同j值的所有可能项，并检查哪个值满足LHS等式。
- 如果在上述步骤中，j的任何候选者都不满足任何值，则打印-1。
C++
// C++ program to calculate discrete logarithm #include<bits/stdc++.h> using namespace std; /* Iterative Function to calculate (x ^ y)%p in O(log y) */ int powmod( int x, int y, int p) { int res = 1; // Initialize result x = x % p; // Update x if it is more than or // equal to p while (y > 0) { // If y is odd, multiply x with result if (y & 1) res = (res*x) % p; // y must be even now y = y>>1; // y = y/2 x = (x*x) % p; } return res; } // Function to calculate k for given a, b, m int discreteLogarithm( int a, int b, int m) { int n = ( int ) sqrt (m) + 1; unordered_map< int , int > value; // Store all values of a^(n*i) of LHS for ( int i = n; i >= 1; --i) value[ powmod (a, i * n, m) ] = i; for ( int j = 0; j < n; ++j) { // Calculate (a ^ j) * b and check // for collision int cur = (powmod (a, j, m) * b) % m; // If collision occurs i.e., LHS = RHS if (value[cur]) { int ans = value[cur] * n - j; // Check whether ans lies below m or not if (ans < m) return ans; } } return -1; } // Driver code int main() { int a = 2, b = 3, m = 5; cout << discreteLogarithm(a, b, m) << endl; a = 3, b = 7, m = 11; cout << discreteLogarithm(a, b, m); } |
JAVA
// Java program to calculate discrete logarithm class GFG{ /* Iterative Function to calculate (x ^ y)%p in O(log y) */ static int powmod( int x, int y, int p) { int res = 1 ; // Initialize result x = x % p; // Update x if it is more than or // equal to p while (y > 0 ) { // If y is odd, multiply x with result if ((y & 1 )> 0 ) res = (res*x) % p; // y must be even now y = y>> 1 ; // y = y/2 x = (x*x) % p; } return res; } // Function to calculate k for given a, b, m static int discreteLogarithm( int a, int b, int m) { int n = ( int ) (Math.sqrt (m) + 1 ); int [] value= new int [m]; // Store all values of a^(n*i) of LHS for ( int i = n; i >= 1 ; --i) value[ powmod (a, i * n, m) ] = i; for ( int j = 0 ; j < n; ++j) { // Calculate (a ^ j) * b and check // for collision int cur = (powmod (a, j, m) * b) % m; // If collision occurs i.e., LHS = RHS if (value[cur]> 0 ) { int ans = value[cur] * n - j; // Check whether ans lies below m or not if (ans < m) return ans; } } return - 1 ; } // Driver code public static void main(String[] args) { int a = 2 , b = 3 , m = 5 ; System.out.println(discreteLogarithm(a, b, m)); a = 3 ; b = 7 ; m = 11 ; System.out.println(discreteLogarithm(a, b, m)); } } // This code is contributed by mits |
Python3
# Python3 program to calculate # discrete logarithm import math; # Iterative Function to calculate # (x ^ y)%p in O(log y) def powmod(x, y, p): res = 1 ; # Initialize result x = x % p; # Update x if it is more # than or equal to p while (y > 0 ): # If y is odd, multiply x with result if (y & 1 ): res = (res * x) % p; # y must be even now y = y >> 1 ; # y = y/2 x = (x * x) % p; return res; # Function to calculate k for given a, b, m def discreteLogarithm(a, b, m): n = int (math.sqrt(m) + 1 ); value = [ 0 ] * m; # Store all values of a^(n*i) of LHS for i in range (n, 0 , - 1 ): value[ powmod (a, i * n, m) ] = i; for j in range (n): # Calculate (a ^ j) * b and check # for collision cur = (powmod (a, j, m) * b) % m; # If collision occurs i.e., LHS = RHS if (value[cur]): ans = value[cur] * n - j; # Check whether ans lies below m or not if (ans < m): return ans; return - 1 ; # Driver code a = 2 ; b = 3 ; m = 5 ; print (discreteLogarithm(a, b, m)); a = 3 ; b = 7 ; m = 11 ; print (discreteLogarithm(a, b, m)); # This code is contributed by mits |
C#
// C# program to calculate discrete logarithm using System; class GFG{ /* Iterative Function to calculate (x ^ y)%p in O(log y) */ static int powmod( int x, int y, int p) { int res = 1; // Initialize result x = x % p; // Update x if it is more than or // equal to p while (y > 0) { // If y is odd, multiply x with result if ((y & 1)>0) res = (res*x) % p; // y must be even now y = y>>1; // y = y/2 x = (x*x) % p; } return res; } // Function to calculate k for given a, b, m static int discreteLogarithm( int a, int b, int m) { int n = ( int ) (Math.Sqrt (m) + 1); int [] value= new int [m]; // Store all values of a^(n*i) of LHS for ( int i = n; i >= 1; --i) value[ powmod (a, i * n, m) ] = i; for ( int j = 0; j < n; ++j) { // Calculate (a ^ j) * b and check // for collision int cur = (powmod (a, j, m) * b) % m; // If collision occurs i.e., LHS = RHS if (value[cur]>0) { int ans = value[cur] * n - j; // Check whether ans lies below m or not if (ans < m) return ans; } } return -1; } // Driver code static void Main() { int a = 2, b = 3, m = 5; Console.WriteLine(discreteLogarithm(a, b, m)); a = 3; b = 7; m = 11; Console.WriteLine(discreteLogarithm(a, b, m)); } } // This code is contributed by mits |
PHP
<?php // PHP program to calculate // discrete logarithm // Iterative Function to calculate // (x ^ y)%p in O(log y) function powmod( $x , $y , $p ) { $res = 1; // Initialize result $x = $x % $p ; // Update x if it is more // than or equal to p while ( $y > 0) { // If y is odd, multiply x with result if ( $y & 1) $res = ( $res * $x ) % $p ; // y must be even now $y = $y >> 1; // y = y/2 $x = ( $x * $x ) % $p ; } return $res ; } // Function to calculate k for given a, b, m function discreteLogarithm( $a , $b , $m ) { $n = (int)sqrt( $m ) + 1; $value = array_fill (0, $m , NULL); // Store all values of a^(n*i) of LHS for ( $i = $n ; $i >= 1; -- $i ) $value [ powmod ( $a , $i * $n , $m ) ] = $i ; for ( $j = 0; $j < $n ; ++ $j ) { // Calculate (a ^ j) * b and check // for collision $cur = (powmod ( $a , $j , $m ) * $b ) % $m ; // If collision occurs i.e., LHS = RHS if ( $value [ $cur ]) { $ans = $value [ $cur ] * $n - $j ; // Check whether ans lies below m or not if ( $ans < $m ) return $ans ; } } return -1; } // Driver code $a = 2; $b = 3; $m = 5; echo discreteLogarithm( $a , $b , $m ), "" ; $a = 3; $b = 7; $m = 11; echo discreteLogarithm( $a , $b , $m ), "" ; // This code is contributed by ajit. ?> |
Javascript
<script> // Javascript program to calculate // discrete logarithm /* Iterative Function to calculate (x ^ y)%p in O(log y) */ function powmod(x, y, p) { // Initialize result let res = 1; // Update x if it is more // than or // equal to p x = x % p; while (y > 0) { // If y is odd, multiply x // with result if ((y & 1)>0) res = (res*x) % p; // y must be even now y = y>>1; // y = y/2 x = (x*x) % p; } return res; } // Function to calculate // k for given a, b, m function discreteLogarithm(a, b, m) { let n = (parseInt(Math.sqrt(m), 10) + 1); let value = new Array(m); value.fill(0); // Store all values of a^(n*i) of LHS for (let i = n; i >= 1; --i) value[ powmod (a, i * n, m) ] = i; for (let j = 0; j < n; ++j) { // Calculate (a ^ j) * b and check // for collision let cur = (powmod (a, j, m) * b) % m; // If collision occurs // i.e., LHS = RHS if (value[cur]>0) { let ans = value[cur] * n - j; // Check whether ans lies // below m or not if (ans < m) return ans; } } return -1; } let a = 2, b = 3, m = 5; document.write( discreteLogarithm(a, b, m) + "</br>" ); a = 3; b = 7; m = 11; document.write( discreteLogarithm(a, b, m) + "</br>" ); </script> |
输出：
3-1
时间复杂性： O（平方米）*对数（b）） 辅助空间： O（平方米） 一个可能的改进是在算法的第二阶段去掉二进制指数或log（b）因子。这可以通过将每次乘以“a”的变量保持为“an”来实现。让我们看看这个节目来了解更多。
C++
// C++ program to calculate discrete logarithm #include<bits/stdc++.h> using namespace std; int discreteLogarithm( int a, int b, int m) { int n = ( int ) sqrt (m) + 1; // Calculate a ^ n int an = 1; for ( int i = 0; i<n; ++i) an = (an * a) % m; unordered_map< int , int > value; // Store all values of a^(n*i) of LHS for ( int i = 1, cur = an; i<= n; ++i) { if (! value[ cur ]) value[ cur ] = i; cur = (cur * an) % m; } for ( int i = 0, cur = b; i<= n; ++i) { // Calculate (a ^ j) * b and check // for collision if (value[cur]) { int ans = value[cur] * n - i; if (ans < m) return ans; } cur = (cur * a) % m; } return -1; } // Driver code int main() { int a = 2, b = 3, m = 5; cout << discreteLogarithm(a, b, m) << endl; a = 3, b = 7, m = 11; cout << discreteLogarithm(a, b, m); } |
JAVA
// Java program to calculate discrete logarithm class GFG { static int discreteLogarithm( int a, int b, int m) { int n = ( int ) (Math.sqrt (m) + 1 ); // Calculate a ^ n int an = 1 ; for ( int i = 0 ; i < n; ++i) an = (an * a) % m; int [] value= new int [m]; // Store all values of a^(n*i) of LHS for ( int i = 1 , cur = an; i <= n; ++i) { if (value[ cur ] == 0 ) value[ cur ] = i; cur = (cur * an) % m; } for ( int i = 0 , cur = b; i <= n; ++i) { // Calculate (a ^ j) * b and check // for collision if (value[cur] > 0 ) { int ans = value[cur] * n - i; if (ans < m) return ans; } cur = (cur * a) % m; } return - 1 ; } // Driver code public static void main(String[] args) { int a = 2 , b = 3 , m = 5 ; System.out.println(discreteLogarithm(a, b, m)); a = 3 ; b = 7 ; m = 11 ; System.out.println(discreteLogarithm(a, b, m)); } } // This code is contributed by mits |
Python3
# Python3 program to calculate # discrete logarithm import math; def discreteLogarithm(a, b, m): n = int (math.sqrt (m) + 1 ); # Calculate a ^ n an = 1 ; for i in range (n): an = (an * a) % m; value = [ 0 ] * m; # Store all values of a^(n*i) of LHS cur = an; for i in range ( 1 , n + 1 ): if (value[ cur ] = = 0 ): value[ cur ] = i; cur = (cur * an) % m; cur = b; for i in range (n + 1 ): # Calculate (a ^ j) * b and check # for collision if (value[cur] > 0 ): ans = value[cur] * n - i; if (ans < m): return ans; cur = (cur * a) % m; return - 1 ; # Driver code a = 2 ; b = 3 ; m = 5 ; print (discreteLogarithm(a, b, m)); a = 3 ; b = 7 ; m = 11 ; print (discreteLogarithm(a, b, m)); # This code is contributed by mits |
C#
// C# program to calculate discrete logarithm using System; class GFG { static int discreteLogarithm( int a, int b, int m) { int n = ( int ) (Math.Sqrt (m) + 1); // Calculate a ^ n int an = 1; for ( int i = 0; i < n; ++i) an = (an * a) % m; int [] value = new int [m]; // Store all values of a^(n*i) of LHS for ( int i = 1, cur = an; i<= n; ++i) { if (value[ cur ] == 0) value[ cur ] = i; cur = (cur * an) % m; } for ( int i = 0, cur = b; i<= n; ++i) { // Calculate (a ^ j) * b and check // for collision if (value[cur] > 0) { int ans = value[cur] * n - i; if (ans < m) return ans; } cur = (cur * a) % m; } return -1; } // Driver code static void Main() { int a = 2, b = 3, m = 5; Console.WriteLine(discreteLogarithm(a, b, m)); a = 3; b = 7; m = 11; Console.WriteLine(discreteLogarithm(a, b, m)); } } // This code is contributed by mits |
PHP
<?php // PHP program to calculate discrete logarithm function discreteLogarithm( $a , $b , $m ) { $n = (int)sqrt ( $m ) + 1; // Calculate a ^ n $an = 1; for ( $i = 0; $i < $n ; ++ $i ) $an = ( $an * $a ) % $m ; $value = array_fill (0, $m , NULL); // Store all values of a^(n*i) of LHS for ( $i = 1, $cur = $an ; $i <= $n ; ++ $i ) { if (! $value [ $cur ]) $value [ $cur ] = $i ; $cur = ( $cur * $an ) % $m ; } for ( $i = 0, $cur = $b ; $i <= $n ; ++ $i ) { // Calculate (a ^ j) * b and check // for collision if ( $value [ $cur ]) { $ans = $value [ $cur ] * $n - $i ; if ( $ans < $m ) return $ans ; } $cur = ( $cur * $a ) % $m ; } return -1; } // Driver code $a = 2; $b = 3; $m = 5; echo discreteLogarithm( $a , $b , $m ), "" ; $a = 3; $b = 7; $m = 11; echo discreteLogarithm( $a , $b , $m ); // This code is contributed by ajit. ?> |
Javascript
<script> // Javascript program to calculate // discrete logarithm function discreteLogarithm(a, b, m) { let n = parseInt(Math.sqrt(m), 10) + 1; // Calculate a ^ n let an = 1; for (let i = 0; i < n; ++i) an = (an * a) % m; let value = new Array(m); value.fill(0); // Store all values of a^(n*i) of LHS for (let i = 1, cur = an; i<= n; ++i) { if (value[ cur ] == 0) value[ cur ] = i; cur = (cur * an) % m; } for (let i = 0, cur = b; i<= n; ++i) { // Calculate (a ^ j) * b and check // for collision if (value[cur] > 0) { let ans = value[cur] * n - i; if (ans < m) return ans; } cur = (cur * a) % m; } return -1; } let a = 2, b = 3, m = 5; document.write(discreteLogarithm(a, b, m) + "</br>" ); a = 3; b = 7; m = 11; document.write(discreteLogarithm(a, b, m)); </script> |
输出：
3-1
时间复杂性： O（平方米） 辅助空间： O（平方米） 参考： http://e-maxx-eng.appspot.com/algebra/discrete-log.html https://en.wikipedia.org/wiki/Baby-step_giant-step 本文由 Shubham Bansal .如果你喜欢GeekSforgek，并想贡献自己的力量，你也可以使用 写极客。组织 或者把你的文章寄去评论-team@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上，并帮助其他极客。
© 版权声明
文章版权归作者所有，未经允许请勿转载。
THE END
![关于”PostgreSQL错误：关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)
