给定一组n个整数，其中n≤40。他们每人最多10人 12 ，确定总和小于或等于S的最大和子集，其中S<=10 18 .
null
例子：
Input : set[] = {45, 34, 4, 12, 5, 2} and S = 42Output : 41Maximum possible subset sum is 41 which can be obtained by summing 34, 5 and 2.Input : Set[] = {3, 34, 4, 12, 5, 2} and S = 10Output : 10Maximum possible subset sum is 10 which can be obtained by summing 2, 3 and 5.
解决这个问题的蛮力方法是找到N个整数的所有可能子集和，检查它是否小于或等于S，并用最大和跟踪这样的子集。使用这种方法的时间复杂度为O（2 N )n最多是40。2. 40 将是相当大的，因此我们需要找到更优化的方法。
在中间相遇 是一种搜索技术，当输入很小时使用，但不会小到可以使用蛮力。就像“分而治之”一样，它将问题一分为二，分别解决，然后合并。但是我们不能像分而治之一样应用在中间，因为我们没有和原来的问题有相同的结构。
- 将整数集拆分为2个子集，例如A和B。A有前n/2个整数，B有剩余整数。
- 在集合A中找到所有可能的整数子集和，并将其存储在数组X中。同样，在集合B中计算所有可能的整数子集和，并将其存储在数组Y中。因此，数组X和Y的大小最多为2 n/2 .
- 现在合并这两个子问题。从数组X和Y中找出组合，使它们的和小于或等于S。
- 一种方法是简单地对数组Y的所有元素进行迭代，以检查数组X的每个元素是否存在这样的组合。这将需要O（（2） n/2 ) 2. )这相当于O（2 N ).
- 为了降低复杂性，首先对数组Y进行排序，然后对X的每个元素进行迭代，对于X中的每个元素X，使用二进制搜索来查找Y中的最大元素Y，这样X+Y<=S。
- 这里的二进制搜索有助于将复杂性从2降低到2 N 到2 n/2 日志（2） n/2 )相当于2 n/2 N
- 因此，我们的最终运行时间是O（2） n/2 n） 。
C++
// C++ program to demonstrate working of Meet in the // Middle algorithm for maximum subset sum problem. #include <bits/stdc++.h> using namespace std; typedef long long int ll; ll X[2000005],Y[2000005]; // Find all possible sum of elements of a[] and store // in x[] void calcsubarray(ll a[], ll x[], int n, int c) { for ( int i=0; i<(1<<n); i++) { ll s = 0; for ( int j=0; j<n; j++) if (i & (1<<j)) s += a[j+c]; x[i] = s; } } // Returns the maximum possible sum less or equal to S ll solveSubsetSum(ll a[], int n, ll S) { // Compute all subset sums of first and second // halves calcsubarray(a, X, n/2, 0); calcsubarray(a, Y, n-n/2, n/2); int size_X = 1<<(n/2); int size_Y = 1<<(n-n/2); // Sort Y (we need to do doing binary search in it) sort(Y, Y+size_Y); // To keep track of the maximum sum of a subset // such that the maximum sum is less than S ll max = 0; // Traverse all elements of X and do Binary Search // for a pair in Y with maximum sum less than S. for ( int i=0; i<size_X; i++) { if (X[i] <= S) { // lower_bound() returns the first address // which has value greater than or equal to // S-X[i]. int p = lower_bound(Y, Y+size_Y, S-X[i]) - Y; // If S-X[i] was not in array Y then decrease // p by 1 if (p == size_Y || Y[p] != (S-X[i])) p--; if ((Y[p]+X[i]) > max) max = Y[p]+X[i]; } } return max; } // Driver code int main() { ll a[] = {3, 34, 4, 12, 5, 2}; int n= sizeof (a)/ sizeof (a[0]); ll S = 10; printf ( "Largest value smaller than or equal to given " "sum is %lld" , solveSubsetSum(a,n,S)); return 0; } |
JAVA
// Java program to demonstrate working of // Meet in the Middle algorithm for // maximum subset sum problem import java.util.*; import java.lang.*; import java.io.*; class GFG{ static long X[] = new long [ 2000005 ]; static long Y[] = new long [ 2000005 ]; // Find all possible sum of elements of a[] // and store in x[] static void calcsubarray( long a[], long x[], int n, int c) { for ( int i = 0 ; i < ( 1 << n); i++) { long s = 0 ; for ( int j = 0 ; j < n; j++) if ((i & ( 1 << j)) == 1 ) s += a[j + c]; x[i] = s; } } // Returns the maximum possible sum // less or equal to S static long solveSubsetSum( long a[], int n, long S) { // Compute all subset sums of first and second // halves calcsubarray(a, X, n / 2 , 0 ); calcsubarray(a, Y, n - n / 2 , n / 2 ); int size_X = 1 << (n / 2 ); int size_Y = 1 << (n - n / 2 ); // Sort Y (we need to do doing // binary search in it) Arrays.sort(Y); // To keep track of the maximum sum // of a subset such that the maximum // sum is less than S long max = 0 ; // Traverse all elements of X and do // Binary Search for a pair in Y with // maximum sum less than S. for ( int i = 0 ; i < size_X; i++) { if (X[i] <= S) { // lower_bound() returns the first address // which has value greater than or equal to // S-X[i]. int p = lower_bound(Y, S - X[i]); // If S-X[i] was not in array Y then // decrease p by 1 if (p == size_Y || Y[p] != (S - X[i])) p--; if ((Y[p] + X[i]) > max) max = Y[p] + X[i]; } } return max; } static int lower_bound( long a[], long x) { // x is the target value or key int l = - 1 , r = a.length; while (l + 1 < r) { int m = (l + r) >>> 1 ; if (a[m] >= x) r = m; else l = m; } return r; } // Driver code public static void main (String[] args) { long a[] = { 3 , 34 , 4 , 12 , 5 , 2 }; int n = a.length; long S = 10 ; System.out.println( "Largest value smaller " + "than or equal to given " + "sum is " + solveSubsetSum(a, n, S)); } } // This code is contributed by jyoti369 |
Python3
# Python program to demonstrate working of Meet in the # Middle algorithm for maximum subset sum problem. from typing import List import bisect X = [ 0 ] * 2000005 Y = [ 0 ] * 2000005 # Find all possible sum of elements of a[] and store # in x[] def calcsubarray(a: List [ int ], x: List [ int ], n: int , c: int ) - > None : for i in range (( 1 << n)): s = 0 for j in range (n): if (i & ( 1 << j)): s + = a[j + c] x[i] = s # Returns the maximum possible sum less or equal to S def solveSubsetSum(a: List [ int ], n: int , S: int ) - > int : global Y # Compute all subset sums of first and second # halves calcsubarray(a, X, n / / 2 , 0 ) calcsubarray(a, Y, n - n / / 2 , n / / 2 ) size_X = 1 << (n / / 2 ) size_Y = 1 << (n - n / / 2 ) # Sort Y (we need to do doing binary search in it) YY = Y[:size_Y] YY.sort() Y = YY # To keep track of the maximum sum of a subset # such that the maximum sum is less than S maxx = 0 # Traverse all elements of X and do Binary Search # for a pair in Y with maximum sum less than S. for i in range (size_X): if (X[i] < = S): # lower_bound() returns the first address # which has value greater than or equal to # S-X[i]. p = bisect.bisect_left(Y, S - X[i]) # If S-X[i] was not in array Y then decrease # p by 1 if (p = = size_Y or (p < size_Y and Y[p] ! = (S - X[i]))): p - = 1 if ((Y[p] + X[i]) > maxx): maxx = Y[p] + X[i] return maxx # Driver code if __name__ = = "__main__" : a = [ 3 , 34 , 4 , 12 , 5 , 2 ] n = len (a) S = 10 print ( "Largest value smaller than or equal to given sum is {}" . format ( solveSubsetSum(a, n, S))) # This code is contributed by sanjeev2552 |
C#
// C# program to demonstrate working of // Meet in the Middle algorithm for // maximum subset sum problem using System; public class GFG { static long [] X = new long [2000005]; static long [] Y = new long [2000005]; // Find all possible sum of elements of a[] // and store in x[] static void calcsubarray( long [] a, long [] x, int n, int c) { for ( int i = 0; i < (1 << n); i++) { long s = 0; for ( int j = 0; j < n; j++) if ((i & (1 << j)) == 1) s += a[j + c]; x[i] = s; } } // Returns the maximum possible sum // less or equal to S static long solveSubsetSum( long [] a, int n, long S) { // Compute all subset sums of first and second // halves calcsubarray(a, X, n / 2, 0); calcsubarray(a, Y, n - n / 2, n / 2); int size_X = 1 << (n / 2); int size_Y = 1 << (n - n / 2); // Sort Y (we need to do doing // binary search in it) Array.Sort(Y); // To keep track of the maximum sum // of a subset such that the maximum // sum is less than S long max = 0; // Traverse all elements of X and do // Binary Search for a pair in Y with // maximum sum less than S. for ( int i = 0; i < size_X; i++) { if (X[i] <= S) { // lower_bound() returns the first address // which has value greater than or equal to // S-X[i]. int p = lower_bound(Y, S - X[i]); // If S-X[i] was not in array Y then // decrease p by 1 if (p == size_Y || Y[p] != (S - X[i])) p--; if ((Y[p] + X[i]) > max) max = Y[p] + X[i]; } } return max; } static int lower_bound( long [] a, long x) { // x is the target value or key int l = -1, r = a.Length; while (l + 1 < r) { int m = (l + r) >> 1; if (a[m] >= x) r = m; else l = m; } return r; } // Driver code static public void Main () { long [] a = { 3, 34, 4, 12, 5, 2 }; int n = a.Length; long S = 10; Console.WriteLine( "Largest value smaller " + "than or equal to given " + "sum is " + solveSubsetSum(a, n, S)); } } // This code is contributed by Dharanendra L V. |
Javascript
<script> // Javascript program to demonstrate working of // Meet in the Middle algorithm for // maximum subset sum problem let X = new Array(2000005); let Y = new Array(2000005); for (let i = 0; i < 2000005; i++) { X[i] = 0; Y[i] = 0; } // Find all possible sum of elements of a[] // and store in x[] function calcsubarray(a, x, n, c) { for (let i = 0; i < (1 << n); i++) { let s = 0; for (let j = 0; j < n; j++) if ((i & (1 << j)) == 1) s += a[j + c]; x[i] = s; } } // Returns the maximum possible sum // less or equal to S function solveSubsetSum(a,n,S) { // Compute all subset sums of first and second // halves calcsubarray(a, X, Math.floor(n / 2), 0); calcsubarray(a, Y, n - Math.floor(n / 2), Math.floor(n / 2)); let size_X = 1 << Math.floor(n / 2); let size_Y = 1 << (n - Math.floor(n / 2)); // Sort Y (we need to do doing // binary search in it) Y.sort( function (a,b){ return a-b;}); // To keep track of the maximum sum // of a subset such that the maximum // sum is less than S let max = 0; // Traverse all elements of X and do // Binary Search for a pair in Y with // maximum sum less than S. for (let i = 0; i < size_X; i++) { if (X[i] <= S) { // lower_bound() returns the first address // which has value greater than or equal to // S-X[i]. let p = lower_bound(Y, S - X[i]); // If S-X[i] was not in array Y then // decrease p by 1 if (p == size_Y || Y[p] != (S - X[i])) p--; if ((Y[p] + X[i]) > max) max = Y[p] + X[i]; } } return max; } function lower_bound(a,x) { // x is the target value or key let l = -1, r = a.length; while (l + 1 < r) { let m = (l + r) >>> 1; if (a[m] >= x) r = m; else l = m; } return r; } // Driver code let a=[3, 34, 4, 12, 5, 2 ]; let n = a.length; let S = 10; document.write( "Largest value smaller " + "than or equal to given " + "sum is " + solveSubsetSum(a, n, S)+ "<br>" ); // This code is contributed by avanitrachhadiya2155 </script> |
输出：
Largest value smaller than or equal to given sum is 10
参考：
时间复杂性： O( 
) 辅助空间： O( 
) 本文由 马杜尔·莫迪 .如果你喜欢GeekSforgek，并想贡献自己的力量，你也可以写一篇文章，然后将文章邮寄给评论-team@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上，并帮助其他极客。 如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请写评论
© 版权声明
文章版权归作者所有，未经允许请勿转载。
THE END
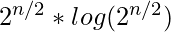
![关于”PostgreSQL错误：关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)
