这个 中点 圆绘制算法是一种用于确定栅格化圆所需点的算法。
我们使用 中点 计算圆中所有周长点的算法 第一卦限 然后把它们和其他八分之一的镜像点一起打印出来。这将起作用,因为一个圆围绕其中心对称。

该算法与 中点线生成算法 这里,只有边界条件不同。
对于任何给定的像素(x,y),下一个要绘制的像素是 (x,y+1) 或 (x-1,y+1) 。这可以通过以下步骤来决定。
- 找到中点 P 两个可能的像素,即(x-0.5,y+1)
- 如果 P 在圆周长内或圆周长上,我们绘制像素(x,y+1),否则如果它在外,我们绘制像素(x-1,y+1)
边界条件: 中点是否位于圆内或圆外,可通过以下公式确定:-
给定一个以(0,0)为中心、半径r和点p(x,y)的圆 F(p)=x 2. +y 2. –r 2. 如果F(p)<0,则点位于圆内 F(p)=0,点在周长上 F(p)>0,点在圆外

在我们的程序中,我们用p来表示F(p)。p的值是在两个竞争像素的中点计算的,即(x-0.5,y+1)。每个像素都用下标k来描述。
P K =(X) K — 0.5) 2. +(y) K + 1) 2. –r 2. 现在 十、 k+1 =x K 或者x k-1 Y k+1 =y K +1 ∴ P k+1 =(x) k+1 – 0.5) 2. +(y) k+1 +1) 2. –r 2. =(x) k+1 – 0.5) 2. +[(y) K +1) + 1] 2. –r 2. =(x) k+1 – 0.5) 2. +(y) K +1) 2. +2(y) K +1)+1-r 2. =(x) k+1 – 0.5) 2. +[–(x) K – 0.5) 2. +(十) K – 0.5) 2. ]+(y) K + 1) 2. –r 2. +(y) K + 1) + 1 =P K +(十) k+1 – 0.5) 2. –(x) K – 0.5) 2. +2(y) K + 1) + 1 =P K +(十) 2. k+1 –x2 K ) 2. +(十) k+1 –x K ) 2. +2(y) K + 1) + 1 =P K +2(y) K +1) +1,当P K <=0,即中点在圆内 (十) k+1 =x K ) P K +2(y) K +1) -2(x) K -1)+1,当P K >0,即中点在圆外(x k+1 =x K -1)
要绘制的第一个点是x轴上的(r,0)。P的初始值计算如下:-
P1=(r–0.5) 2. + (0+1) 2. –r 2. =1.25–r =1-r(四舍五入时)
例如:
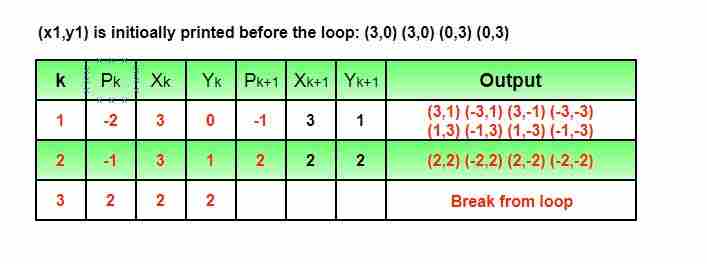
Input : Centre -> (0, 0), Radius -> 3Output : (3, 0) (3, 0) (0, 3) (0, 3) (3, 1) (-3, 1) (3, -1) (-3, -1) (1, 3) (-1, 3) (1, -3) (-1, -3) (2, 2) (-2, 2) (2, -2) (-2, -2)
Input : Centre -> (4, 4), Radius -> 2Output : (6, 4) (6, 4) (4, 6) (4, 6) (6, 5) (2, 5) (6, 3) (2, 3) (5, 6) (3, 6) (5, 2) (3, 2)
CPP
// C++ program for implementing // Mid-Point Circle Drawing Algorithm #include<iostream> using namespace std; // Implementing Mid-Point Circle Drawing Algorithm void midPointCircleDraw( int x_centre, int y_centre, int r) { int x = r, y = 0; // Printing the initial point on the axes // after translation cout << "(" << x + x_centre << ", " << y + y_centre << ") " ; // When radius is zero only a single // point will be printed if (r > 0) { cout << "(" << x + x_centre << ", " << -y + y_centre << ") " ; cout << "(" << y + x_centre << ", " << x + y_centre << ") " ; cout << "(" << -y + x_centre << ", " << x + y_centre << ")" ; } // Initialising the value of P int P = 1 - r; while (x > y) { y++; // Mid-point is inside or on the perimeter if (P <= 0) P = P + 2*y + 1; // Mid-point is outside the perimeter else { x--; P = P + 2*y - 2*x + 1; } // All the perimeter points have already been printed if (x < y) break ; // Printing the generated point and its reflection // in the other octants after translation cout << "(" << x + x_centre << ", " << y + y_centre << ") " ; cout << "(" << -x + x_centre << ", " << y + y_centre << ") " ; cout << "(" << x + x_centre << ", " << -y + y_centre << ") " ; cout << "(" << -x + x_centre << ", " << -y + y_centre << ")" ; // If the generated point is on the line x = y then // the perimeter points have already been printed if (x != y) { cout << "(" << y + x_centre << ", " << x + y_centre << ") " ; cout << "(" << -y + x_centre << ", " << x + y_centre << ") " ; cout << "(" << y + x_centre << ", " << -x + y_centre << ") " ; cout << "(" << -y + x_centre << ", " << -x + y_centre << ")" ; } } } // Driver code int main() { // To draw a circle of radius 3 centered at (0, 0) midPointCircleDraw(0, 0, 3); return 0; } |
C
// C program for implementing // Mid-Point Circle Drawing Algorithm #include<stdio.h> // Implementing Mid-Point Circle Drawing Algorithm void midPointCircleDraw( int x_centre, int y_centre, int r) { int x = r, y = 0; // Printing the initial point on the axes // after translation printf ( "(%d, %d) " , x + x_centre, y + y_centre); // When radius is zero only a single // point will be printed if (r > 0) { printf ( "(%d, %d) " , x + x_centre, -y + y_centre); printf ( "(%d, %d) " , y + x_centre, x + y_centre); printf ( "(%d, %d)" , -y + x_centre, x + y_centre); } // Initialising the value of P int P = 1 - r; while (x > y) { y++; // Mid-point is inside or on the perimeter if (P <= 0) P = P + 2*y + 1; // Mid-point is outside the perimeter else { x--; P = P + 2*y - 2*x + 1; } // All the perimeter points have already been printed if (x < y) break ; // Printing the generated point and its reflection // in the other octants after translation printf ( "(%d, %d) " , x + x_centre, y + y_centre); printf ( "(%d, %d) " , -x + x_centre, y + y_centre); printf ( "(%d, %d) " , x + x_centre, -y + y_centre); printf ( "(%d, %d)" , -x + x_centre, -y + y_centre); // If the generated point is on the line x = y then // the perimeter points have already been printed if (x != y) { printf ( "(%d, %d) " , y + x_centre, x + y_centre); printf ( "(%d, %d) " , -y + x_centre, x + y_centre); printf ( "(%d, %d) " , y + x_centre, -x + y_centre); printf ( "(%d, %d)" , -y + x_centre, -x + y_centre); } } } // Driver code int main() { // To draw a circle of radius 3 centered at (0, 0) midPointCircleDraw(0, 0, 3); return 0; } |
JAVA
// Java program for implementing // Mid-Point Circle Drawing Algorithm class GFG { // Implementing Mid-Point Circle // Drawing Algorithm static void midPointCircleDraw( int x_centre, int y_centre, int r) { int x = r, y = 0 ; // Printing the initial point // on the axes after translation System.out.print( "(" + (x + x_centre) + ", " + (y + y_centre) + ")" ); // When radius is zero only a single // point will be printed if (r > 0 ) { System.out.print( "(" + (x + x_centre) + ", " + (-y + y_centre) + ")" ); System.out.print( "(" + (y + x_centre) + ", " + (x + y_centre) + ")" ); System.out.println( "(" + (-y + x_centre) + ", " + (x + y_centre) + ")" ); } // Initialising the value of P int P = 1 - r; while (x > y) { y++; // Mid-point is inside or on the perimeter if (P <= 0 ) P = P + 2 * y + 1 ; // Mid-point is outside the perimeter else { x--; P = P + 2 * y - 2 * x + 1 ; } // All the perimeter points have already // been printed if (x < y) break ; // Printing the generated point and its // reflection in the other octants after // translation System.out.print( "(" + (x + x_centre) + ", " + (y + y_centre) + ")" ); System.out.print( "(" + (-x + x_centre) + ", " + (y + y_centre) + ")" ); System.out.print( "(" + (x + x_centre) + ", " + (-y + y_centre) + ")" ); System.out.println( "(" + (-x + x_centre) + ", " + (-y + y_centre) + ")" ); // If the generated point is on the // line x = y then the perimeter points // have already been printed if (x != y) { System.out.print( "(" + (y + x_centre) + ", " + (x + y_centre) + ")" ); System.out.print( "(" + (-y + x_centre) + ", " + (x + y_centre) + ")" ); System.out.print( "(" + (y + x_centre) + ", " + (-x + y_centre) + ")" ); System.out.println( "(" + (-y + x_centre) + ", " + (-x + y_centre) + ")" ); } } } // Driver code public static void main(String[] args) { // To draw a circle of radius // 3 centered at (0, 0) midPointCircleDraw( 0 , 0 , 3 ); } } // This code is contributed by Anant Agarwal. |
Python3
# Python3 program for implementing # Mid-Point Circle Drawing Algorithm def midPointCircleDraw(x_centre, y_centre, r): x = r y = 0 # Printing the initial point the # axes after translation print ( "(" , x + x_centre, ", " , y + y_centre, ")" , sep = " ", end = " ") # When radius is zero only a single # point be printed if (r > 0 ) : print ( "(" , x + x_centre, ", " , - y + y_centre, ")" , sep = " ", end = " ") print ( "(" , y + x_centre, ", " , x + y_centre, ")" , sep = " ", end = " ") print ( "(" , - y + x_centre, ", " , x + y_centre, ")" , sep = "") # Initialising the value of P P = 1 - r while x > y: y + = 1 # Mid-point inside or on the perimeter if P < = 0 : P = P + 2 * y + 1 # Mid-point outside the perimeter else : x - = 1 P = P + 2 * y - 2 * x + 1 # All the perimeter points have # already been printed if (x < y): break # Printing the generated point its reflection # in the other octants after translation print ( "(" , x + x_centre, ", " , y + y_centre, ")" , sep = " ", end = " ") print ( "(" , - x + x_centre, ", " , y + y_centre, ")" , sep = " ", end = " ") print ( "(" , x + x_centre, ", " , - y + y_centre, ")" , sep = " ", end = " ") print ( "(" , - x + x_centre, ", " , - y + y_centre, ")" , sep = "") # If the generated point on the line x = y then # the perimeter points have already been printed if x ! = y: print ( "(" , y + x_centre, ", " , x + y_centre, ")" , sep = " ", end = " ") print ( "(" , - y + x_centre, ", " , x + y_centre, ")" , sep = " ", end = " ") print ( "(" , y + x_centre, ", " , - x + y_centre, ")" , sep = " ", end = " ") print ( "(" , - y + x_centre, ", " , - x + y_centre, ")" , sep = "") # Driver Code if __name__ = = '__main__' : # To draw a circle of radius 3 # centered at (0, 0) midPointCircleDraw( 0 , 0 , 3 ) # Contributed by: SHUBHAMSINGH10 # Improved by: siddharthx_07 |
C#
// C# program for implementing Mid-Point // Circle Drawing Algorithm using System; class GFG { // Implementing Mid-Point Circle // Drawing Algorithm static void midPointCircleDraw( int x_centre, int y_centre, int r) { int x = r, y = 0; // Printing the initial point on the // axes after translation Console.Write( "(" + (x + x_centre) + ", " + (y + y_centre) + ")" ); // When radius is zero only a single // point will be printed if (r > 0) { Console.Write( "(" + (x + x_centre) + ", " + (-y + y_centre) + ")" ); Console.Write( "(" + (y + x_centre) + ", " + (x + y_centre) + ")" ); Console.WriteLine( "(" + (-y + x_centre) + ", " + (x + y_centre) + ")" ); } // Initialising the value of P int P = 1 - r; while (x > y) { y++; // Mid-point is inside or on the perimeter if (P <= 0) P = P + 2 * y + 1; // Mid-point is outside the perimeter else { x--; P = P + 2 * y - 2 * x + 1; } // All the perimeter points have already // been printed if (x < y) break ; // Printing the generated point and its // reflection in the other octants after // translation Console.Write( "(" + (x + x_centre) + ", " + (y + y_centre) + ")" ); Console.Write( "(" + (-x + x_centre) + ", " + (y + y_centre) + ")" ); Console.Write( "(" + (x + x_centre) + ", " + (-y + y_centre) + ")" ); Console.WriteLine( "(" + (-x + x_centre) + ", " + (-y + y_centre) + ")" ); // If the generated point is on the // line x = y then the perimeter points // have already been printed if (x != y) { Console.Write( "(" + (y + x_centre) + ", " + (x + y_centre) + ")" ); Console.Write( "(" + (-y + x_centre) + ", " + (x + y_centre) + ")" ); Console.Write( "(" + (y + x_centre) + ", " + (-x + y_centre) + ")" ); Console.WriteLine( "(" + (-y + x_centre) + ", " + (-x + y_centre) + ")" ); } } } // Driver code public static void Main() { // To draw a circle of radius // 3 centered at (0, 0) midPointCircleDraw(0, 0, 3); } } // This code is contributed by nitin mittal. |
PHP
<?php // PHP program for implementing // Mid-Point Circle Drawing Algorithm // Implementing Mid-Point // Circle Drawing Algorithm function midPointCircleDraw( $x_centre , $y_centre , $r ) { $x = $r ; $y = 0; // Printing the initial // point on the axes // after translation echo "(" , $x + $x_centre , "," , $y + $y_centre , ")" ; // When radius is zero only a single // point will be printed if ( $r > 0) { echo "(" , $x + $x_centre , "," , - $y + $y_centre , ")" ; echo "(" , $y + $x_centre , "," , $x + $y_centre , ")" ; echo "(" ,- $y + $x_centre , "," , $x + $y_centre , ")" , "" ; } // Initializing the value of P $P = 1 - $r ; while ( $x > $y ) { $y ++; // Mid-point is inside // or on the perimeter if ( $P <= 0) $P = $P + 2 * $y + 1; // Mid-point is outside // the perimeter else { $x --; $P = $P + 2 * $y - 2 * $x + 1; } // All the perimeter points // have already been printed if ( $x < $y ) break ; // Printing the generated // point and its reflection // in the other octants // after translation echo "(" , $x + $x_centre , "," , $y + $y_centre , ")" ; echo "(" ,- $x + $x_centre , "," , $y + $y_centre , ")" ; echo "(" , $x + $x_centre , "," , - $y + $y_centre , ")" ; echo "(" ,- $x + $x_centre , "," , - $y + $y_centre , ")" , "" ; // If the generated point is // on the line x = y then // the perimeter points have // already been printed if ( $x != $y ) { echo "(" , $y + $x_centre , "," , $x + $y_centre , ")" ; echo "(" ,- $y + $x_centre , "," , $x + $y_centre , ")" ; echo "(" , $y + $x_centre , "," , - $x + $y_centre , ")" ; echo "(" ,- $y + $x_centre , "," , - $x + $y_centre , ")" , "" ; } } } // Driver code // To draw a circle of radius // 3 centered at (0, 0) midPointCircleDraw(0, 0, 3); // This code is contributed by nitin mittal. ?> |
Javascript
<script> // javascript program for implementing // Mid-Point Circle Drawing Algorithm // Implementing Mid-Point Circle // Drawing Algorithm function midPointCircleDraw(x_centre , y_centre , r) { var x = r, y = 0; // Printing the initial point // on the axes after translation document.write( "(" + (x + x_centre) + ", " + (y + y_centre) + ")" ); // When radius is zero only a single // point will be printed if (r > 0) { document.write( "(" + (x + x_centre) + ", " + (-y + y_centre) + ")" ); document.write( "(" + (y + x_centre) + ", " + (x + y_centre) + ")" ); document.write( "(" + (-y + x_centre) + ", " + (x + y_centre) + ")<br/>" ); } // Initialising the value of P var P = 1 - r; while (x > y) { y++; // Mid-point is inside or on the perimeter if (P <= 0) P = P + 2 * y + 1; // Mid-point is outside the perimeter else { x--; P = P + 2 * y - 2 * x + 1; } // All the perimeter points have already // been printed if (x < y) break ; // Printing the generated point and its // reflection in the other octants after // translation document.write( "(" + (x + x_centre) + ", " + (y + y_centre) + ")" ); document.write( "(" + (-x + x_centre) + ", " + (y + y_centre) + ")" ); document.write( "(" + (x + x_centre) + ", " + (-y + y_centre) + ")" ); document.write( "(" + (-x + x_centre) + ", " + (-y + y_centre) + ")<br/>" ); // If the generated point is on the // line x = y then the perimeter points // have already been printed if (x != y) { document.write( "(" + (y + x_centre) + ", " + (x + y_centre) + ")" ); document.write( "(" + (-y + x_centre) + ", " + (x + y_centre) + ")" ); document.write( "(" + (y + x_centre) + ", " + (-x + y_centre) + ")" ); document.write( "(" + (-y + x_centre) + ", " + (-x + y_centre) + ")<br/>" ); } } } // Driver code // To draw a circle of radius // 3 centered at (0, 0) midPointCircleDraw(0, 0, 3); // This code is contributed by umadevi9616 </script> |
输出:
(3, 0) (3, 0) (0, 3) (0, 3)(3, 1) (-3, 1) (3, -1) (-3, -1)(1, 3) (-1, 3) (1, -3) (-1, -3)(2, 2) (-2, 2) (2, -2) (-2, -2)
时间复杂性: O(x–y) 辅助空间: O(1) 参考资料: 中点圆算法 图像参考: 圆的八分之一 , 光栅化圆 ,其他图片是由极客为本文创作的 谢谢 图希娜·辛格 为了改进这篇文章。 本文由 纳巴内特·罗伊 .如果你喜欢GeekSforgek,并想贡献自己的力量,你也可以使用 写极客。组织 或者把你的文章寄去评论-team@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上,并帮助其他极客。 如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写下评论。


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



