给定两点A(x1,y1)和B(x2,y2)的坐标,使得x1
在这篇文章中,我们将讨论中点线绘制算法,这是一种不同于前一篇文章中介绍的Bresenham算法的表示方法。 如中所述 以前的职位 ,对于任何给定/计算的前一个像素P(X P Y P ),则有两个最接近直线的下一个像素候选,E(X P +1,Y P )和NE(X P +1,Y P +1) ( E 代表东方和东方 氖 代表东北)。 在中点算法中,我们执行以下操作。
- 找到两个可能的下一个点的中间点。E(X)的中间 P +1,Y P )和NE(X P +1,Y P +1) 是M(X)吗 p+1 Y P +1/2).
- 如果M在直线上方,则选择E作为下一个点。
- 如果M在直线以下,则选择NE作为下一个点。
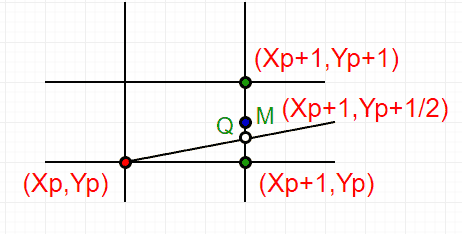
如何确定一个点是在直线上方还是在直线下方? 下面是一些保持算法简单的假设。
- 我们从左到右划一条线。
- x1
- 直线的坡度介于0和1之间。我们从左下角到右上角画一条线。
除上述假设之外的情况可以使用反射来处理。
Let us consider a line y = mx + B. We can re-write the equation as :y = (dy/dx)x + B or (dy)x + B(dx) - y(dx) = 0Let F(x, y) = (dy)x - y(dx) + B(dx) -----(1)Let we are given two end points of a line (underabove assumptions)-> For all points (x,y) on the line, the solution to F(x, y) is 0. -> For all points (x,y) above the line, F(x, y) result in a negative number. -> And for all points (x,y) below the line, F(x, y) result in a positive number.
此关系用于确定相对 M的位置 M=(X) p+1 Y p+1 /2) 所以我们的 决策参数d 是 d=F(M)=F(X) p+1 Y p+1 /2) 如何有效地从d的旧值中发现新值? 为了简单起见,让as把F(x,y)写成ax+by+c。 其中a=dy b=-dx c=B*dx 我们从上面的等式(1)中得到这些值 案例1: 如果选择E,则下一点: dnew=F(X) P +2,Y p+1 /2) =a(X) P +2) +b(Y) p+1 /2) +c dold=a(X) P +1) +b(Y) p+1 /2) +c 两个距离的差值(或增量): DELd=dnew–dold =a(X) P +2) -a(X) P +1) +b(Y) p+1 /2) -b(Y) p+1 /2) +c-c =a(X) P )+2a–a(X) P )–a =a。 因此,dnew=dold+dy(作为a=dy)
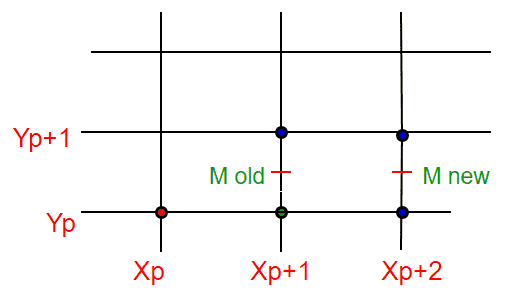
案例2: 如果选择NE,则下一点: dnew=F(X) P +2,Y P +3/2) =a(X) P +2) +b(Y) P +3/2)+c dold=a(X) P +1) +b(Y) P +1/2)+c 两个距离的差值(或增量): DELd=dnew-dold =a(X) P +2) -a(X) P +1) +b(Y) P +3/2-b(Y) P +1/2)+c-c =a(X) P )+2a–a(X) P )–a+b(Y) P )+3/2b–b(Y) P )-1/2b =a+b 因此,dnew=dold+dy–dx。(作为a=dy,b=-dx) 决策参数d0初值的计算: d0=F(X1+1,Y1+1/2) =a(X1+1)+b(Y1+1/2)+c =aX1+bY1+c+a+b/2 =F(X1,Y1)+a+b/2 =a+b/2(如F(X1,Y1)=0) d0=dy–dx/2。(作为a=dy,b=-dx) 算法:
Input (X1,Y1) and (X2,Y2)dy = Y2- Y1dx = X2 - X1// initial value of // decision parameter dif(dy<=dx){d = dy - (dx/2)x = X1 , y = Y1// plot initial given pointPlot(x , y)// iterate through value of Xwhile(x < X2) x = x+1 // 'E' is chosen if (d < 0) d = d + dy // 'NE' is chosen else d = d + dy - dx y = y+1 Plot(x,y)}else if(dx<=dy){d = dx - (dy/2)x = X1 , y = Y1// plot initial given pointPlot(x , y)// iterate through value of Xwhile(y< Y2) y= y+1 // 'E' is chosen if (d < 0) d = d + dx // 'NE' is chosen else d = d + dx - dy x= x+1 Plot(x,y)}
以下是上述理念的实施:
C++
// C++ program for Mid-point line generation #include<bits/stdc++.h> using namespace std; // Header file for including graphics functions // #include<graphics.h> // midPoint function for line generation void midPoint( int X1, int Y1, int X2, int Y2) { // calculate dx & dy int dx = X2 - X1; int dy = Y2 - Y1; if (dy<=dx){ // initial value of decision parameter d int d = dy - (dx/2); int x = X1, y = Y1; // Plot initial given point // putpixel(x,y) can be used to print pixel // of line in graphics cout << x << "," << y << "" ; // iterate through value of X while (x < X2) { x++; // E or East is chosen if (d < 0) d = d + dy; // NE or North East is chosen else { d += (dy - dx); y++; } // Plot intermediate points // putpixel(x,y) is used to print pixel // of line in graphics cout << x << "," << y << "" ; } } else if (dx<dy) { // initial value of decision parameter d int d = dx - (dy/2); int x = X1, y = Y1; // Plot initial given point // putpixel(x,y) can be used to print pixel // of line in graphics cout << x << "," << y << "" ; // iterate through value of X while (y < Y2) { y++; // E or East is chosen if (d < 0) d = d + dx; // NE or North East is chosen // NE or North East is chosen else { d += (dx - dy); x++; } // Plot intermediate points // putpixel(x,y) is used to print pixel // of line in graphics cout << x << "," << y << "" ; } } } // Driver program int main() { // graphics driver and mode // used in graphics.h // int gd = DETECT, gm; // Initialize graphics function // initgraph (&gd, &gm, ""); int X1 = 2, Y1 = 2, X2 = 8, Y2 = 5; midPoint(X1, Y1, X2, Y2); return 0; } |
JAVA
// Java program for Mid-point // line generation class GFG { // midPoint function for line generation static void midPoint( int X1, int Y1, int X2, int Y2) { // calculate dx & dy int dx = X2 - X1; int dy = Y2 - Y1; // initial value of decision // parameter d int d = dy - (dx/ 2 ); int x = X1, y = Y1; // Plot initial given point // putpixel(x,y) can be used to // print pixel of line in graphics System.out.print(x + "," + y + "" ); // iterate through value of X while (x < X2) { x++; // E or East is chosen if (d < 0 ) d = d + dy; // NE or North East is chosen else { d += (dy - dx); y++; } // Plot intermediate points // putpixel(x,y) is used to print // pixel of line in graphics System.out.print(x + "," + y + "" ); } } // Driver code public static void main (String[] args) { int X1 = 2 , Y1 = 2 , X2 = 8 , Y2 = 5 ; midPoint(X1, Y1, X2, Y2); } } // This code is contributed by Anant Agarwal. |
Python 3
# Python3 program for Mid-point # line generation # midPoint function for line generation def midPoint(X1,Y1,X2,Y2): # calculate dx & dy dx = X2 - X1 dy = Y2 - Y1 # initial value of decision parameter d d = dy - (dx / 2 ) x = X1 y = Y1 # Plot initial given point # putpixel(x,y) can be used to print pixel # of line in graphics print (x, "," ,y, "" ) # iterate through value of X while (x < X2): x = x + 1 # E or East is chosen if (d < 0 ): d = d + dy # NE or North East is chosen else : d = d + (dy - dx) y = y + 1 # Plot intermediate points # putpixel(x,y) is used to print pixel # of line in graphics print (x, "," ,y, "" ) # Driver program if __name__ = = '__main__' : X1 = 2 Y1 = 2 X2 = 8 Y2 = 5 midPoint(X1, Y1, X2, Y2) # This code is contributed by ash264 |
C#
// C# program for Mid-point // line generation using System; class GFG { // midPoint function for line // generation static void midPoint( int X1, int Y1, int X2, int Y2) { // calculate dx & dy int dx = X2 - X1; int dy = Y2 - Y1; // initial value of decision // parameter d int d = dy - (dx/2); int x = X1, y = Y1; // Plot initial given point // putpixel(x,y) can be used // to print pixel of line in // graphics Console.Write(x + "," + y + "" ); // iterate through value of X while (x < X2) { x++; // E or East is chosen if (d < 0) d = d + dy; // NE or North East is chosen else { d += (dy - dx); y++; } // Plot intermediate points // putpixel(x,y) is used to print // pixel of line in graphics Console.Write(x + "," + y + "" ); } } // Driver code public static void Main () { int X1 = 2, Y1 = 2, X2 = 8, Y2 = 5; midPoint(X1, Y1, X2, Y2); } } // This code is contributed by nitin mittal. |
PHP
<?php // PHP program for Mid-point // line generation // midPoint function for // line generation function midPoint( $X1 , $Y1 , $X2 , $Y2 ) { // calculate dx & dy $dx = $X2 - $X1 ; $dy = $Y2 - $Y1 ; // initial value of // decision parameter d $d = $dy - ( $dx /2); $x = $X1 ; $y = $Y1 ; // Plot initial given point // putpixel(x,y) can be used // to print pixel of line // in graphics echo $x , "," , $y , "" ; // iterate through // value of X while ( $x < $X2 ) { $x ++; // E or East is chosen if ( $d < 0) $d = $d + $dy ; // NE or North East // is chosen else { $d += ( $dy - $dx ); $y ++; } // Plot intermediate points // putpixel(x,y) is used // to print pixel of // line in graphics echo $x , "," , $y , "" ; } } // Driver Code $X1 = 2; $Y1 = 2; $X2 = 8; $Y2 = 5; midPoint( $X1 , $Y1 , $X2 , $Y2 ); // This code is contributed by nitin mittal. ?> |
Javascript
<script> // JavaScript program for the above approach // midPoint function for line generation function midPoint(X1, Y1, X2, Y2) { // calculate dx & dy let dx = X2 - X1; let dy = Y2 - Y1; // initial value of decision // parameter d let d = dy - (dx/2); let x = X1, y = Y1; // Plot initial given point // putpixel(x,y) can be used to // print pixel of line in graphics document.write(x + "," + y + "<br/>" ); // iterate through value of X while (x < X2) { x++; // E or East is chosen if (d < 0) d = d + dy; // NE or North East is chosen else { d += (dy - dx); y++; } // Plot intermediate points // putpixel(x,y) is used to print // pixel of line in graphics document.write(x + "," + y + "<br/>" ); } } // Driver Code let X1 = 2, Y1 = 2, X2 = 8, Y2 = 5; midPoint(X1, Y1, X2, Y2); // This code is contributed by chinmoy1997pal. </script> |
输出:
2,23,34,35,46,47,58,5
时间复杂性: O(x2-x1) 辅助空间: O(1) 参考资料: http://www.eng.utah.edu/~cs5600/slides/Wk%202%20Lec02_Bresenham。pdf 本文由 希瓦姆·普拉丹(anuj_charm) .如果你喜欢GeekSforgek,并想贡献自己的力量,你也可以使用 写极客。组织 或者把你的文章寄去评论-team@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上,并帮助其他极客。 如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写下评论。


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



