计算机算术|集–2

浮点加减法

• 浮点加法

为了理解浮点加法，首先我们看到十进制实数的加法，因为在这两种情况下都应用了相同的逻辑。

例如 我们必须补充一点 1.1 * 10 ^3. 和 50

我们不能直接将这些数字相加。首先，我们需要对齐指数，然后，我们可以添加显著的。

调整指数后，我们得到 50 = 0.05 * 10 ^三

现在增加了重要的， 0.05 + 1.1 = 1.15

所以，我们终于 (1.1 * 10 ^3. + 50) = 1.15 * 10 ^3.

这里，请注意，我们改变了 50 成功了 0.05 把这些数字加起来。

现在让我们以浮点数加法为例

我们按照以下步骤添加两个数字：

1.调整重要的

2.添加重要的

3.使结果正常化

让这两个数字为准

x=9.75 y=0.5625

将其转换为32位浮点表示，

9.75 的32位格式表示= 0 10000010 00111000000000000000000

0.5625 的32位格式表示= 0 01111110 00100000000000000000000

现在我们得到指数的差值，来知道需要多少位移。

( 10000010 – 01111110 )2 = ( 4. )10

现在，我们将较小数的尾数右移4个单位。

尾数 0.5625 = 1.00100000000000000000000

（请注意，在32位表示法中，小数点前1是可以理解的）

右转 4. 单位，我们有 0.00010010000000000000000

尾数 9.75 = 1. 00111000000000000000000

将两者的尾数相加

0. 00010010000000000000000

+ 1. 00111000000000000000000

————————————————-

1. 01001010000000000000000

在最后的答案中，我们取大数的指数

因此，最终答案包括：

符号位= 0

大数指数= 10000010

尾数= 01001010000000000000000

答案的32位表示= x+y = 0 10000010 01001010000000000000000

• 浮点减法

减法与加法类似，但也有一些不同，比如我们减去尾数，而不是加法，在符号位中，我们把数字的符号放得更大。

让这两个数字成为现实

x=9.75 y=-0.5625

将它们转换为32位浮点表示

9.75 的32位格式表示= 0 10000010 00111000000000000000000

– 0.5625 的32位格式表示= 1 01111110 00100000000000000000000

现在，我们找出指数的差异，来知道需要多少位移。

( 10000010 – 01111110 )2 = ( 4. )10 现在，我们将较小数的尾数右移4个单位。

尾数 – 0.5625 = 1.00100000000000000000000

（请注意，在32位表示法中，小数点前1是可以理解的）

右转 4. 单位， 0.00010010000000000000000

尾数 9.75 = 1. 00111000000000000000000

减去两者的尾数

0. 00010010000000000000000

– 1. 00111000000000000000000

————————————————

1. 00100110000000000000000

签署一个更大的数字= 0

所以，答案终于出来了= x–y=0 100000010 001100000000000000

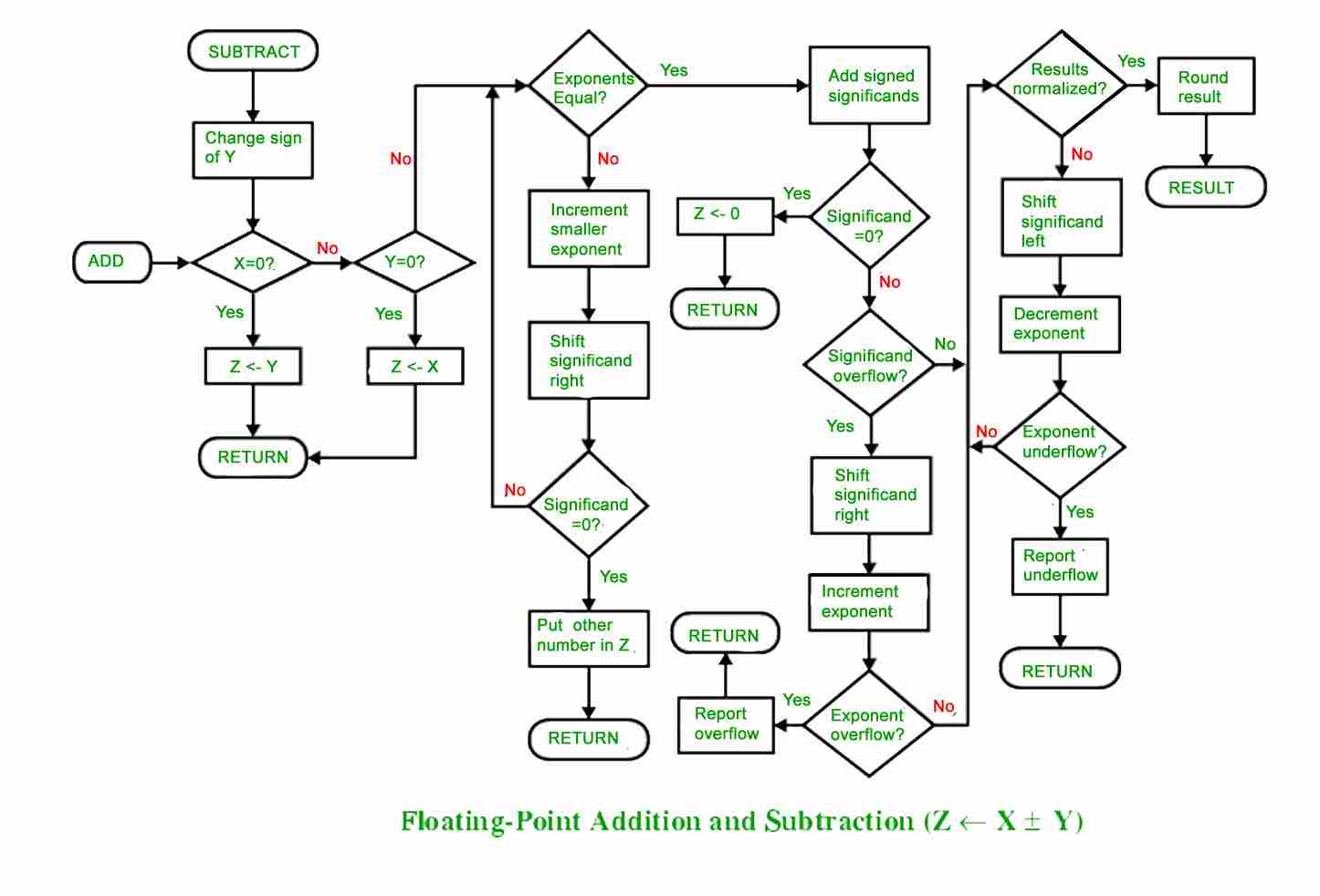
本文由Anuj Batham撰稿。

如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请写评论