计算机算术|集–1

负数表示法

• 符号震级

符号大小是负数的一种非常简单的表示形式。在符号大小中，第一位专用于表示符号，因此称为符号位。

符号位“1”表示负号。

符号位“0”表示正号。

在n位数字的符号幅度表示中，第一位表示符号，其余n-1位表示数字的幅度。

例如

• +25 = 011001

其中11001=25

0代表“+”

• -25 = 111001

其中11001=25

1代表“-”。

符号幅度法表示的数字范围 = -(2 ^n-1 -1） 到+（2） ^n-1 -1） （适用于n位数字）

但符号大小有一个问题，那就是我们有两个0的表示

+0 = 000000

– 0 = 100000

• 2.补码法

要用这种形式表示负数，首先我们需要用简单的正二进制形式表示的数字的1的补码，然后把1加到它上面。

例如：

(-8) 10 = (1000) 2.

1000的1的补码=0111

加上1，0111+1=1000

所以，（-8） 10 = (1000) 2.

请不要对（8）感到困惑 10 =1000和（-8） 10 =1000与4位一样，我们不能表示大于7的正数。所以，1000只代表-8。

由2的补码表示的数字范围= ( -2 ^n-1 到2 ^n-1 – 1)

数字的浮点表示法

• 32位表示浮点数IEEE标准

规范化

• 浮点数通常是标准化的
• 调整指数，使尾数的前导位（MSB）为1
• 因为它总是1，所以没有必要存储它
• 一种科学记数法，将数字标准化为小数点前的一位数字，如十进制中的3.123 x 10 ^3.

例如，我们用32位格式表示3.625。

在二进制中更改3=11

在二进制中更改.625

.625 X 2       1
.25 X 2         0
.5 X 2           1

以二进制指数形式书写

3.625=11.101 X 2 ⁰

论规范化

11.101 X 2 ⁰ =1.1101 X 2 ^1.

关于偏置指数=127+1=128

(128) 10 =(10000000) 2.

为了获得意义

小数点后的数字=1101

扩展到23位=110100000000000000000

设置符号位

因为它是一个正数，所以符号位=0

最后我们根据代表性进行安排

Sign bit      exponent      significand

0 10000000      11010000000000000000000

• 64位表示浮点数IEEE标准

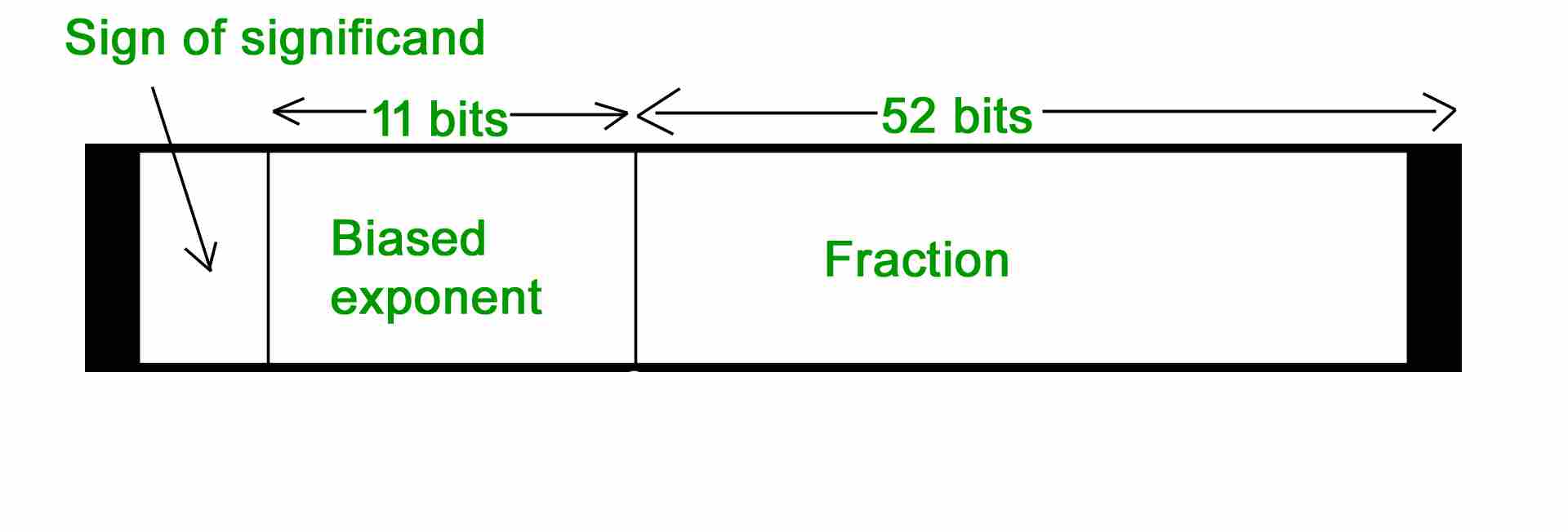同样地，我们遵循相同的过程直到标准化。在那之后，我们加1023来偏置指数。

例如，我们用64位格式表示-3.625。

在二进制中更改3=11

在二进制中更改.625

.625 X 2     1

.25 X 2       0

.5 X 2         1

以二进制指数形式书写

3.625=11.101 X 2 ⁰

论规范化

11.101 X 2 ⁰ =1.1101 X 2 ^1.

关于偏置指数1023+1=1024

(1024) 10 = (10000000000) 2.

所以11位指数=1000000000

52位有效位=110100000000…………。总共52位

设置符号位=1（数字为负数）

最后陈述

1 10000000000 110100000000 …………. 再加上0，总计52位

将浮点转换为十进制

让我们把一个FP数转换成十进制数

1 01111100 11000000000000000000000

IEEE数字的十进制值由以下公式给出：

（1-2s）*（1+f）*2 ^{（e——偏见）}

哪里

• s、 f和e字段在这里取十进制。
• （1-2s）为1或-1，具体取决于符号位0和1
• 将隐式1添加到有效位（分数字段f），如公式所示

同样，对于单精度或双精度，偏差分别为127或1023。

首先将每个字段转换为十进制。

• 符号位s是1
• e字段包含0111100=（124） 10
• 尾数是0.11000…=（0.75） 10

将这些值放入公式中

(1 – 2) * (1 + 0.75) * 2 ^{124 – 127} = ( – 1.75 * 2 ^-3 ) = – 0.21875

本文由Anuj Batham撰稿。

如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请写评论