二进制堆

二进制堆是具有以下属性的二叉树。 1） 这是一个完整的树（除了最后一个级别，所有级别都被完全填充，最后一个级别尽可能地保留所有关键点）。二进制堆的这个特性使它们适合存储在数组中。

2） 二进制堆是最小堆或最大堆。在最小二进制堆中，根上的密钥必须是二进制堆中所有密钥中的最小密钥。对于二叉树中的所有节点，相同的属性必须递归为真。最大二进制堆类似于最小堆。

最小堆的示例：

            10                      10
         /                     /         
       20        100          15         30  
      /                      /          /  
    30                     40    50    100   40

二进制堆是如何表示的？ 二进制堆是一个完整的二叉树。二进制堆通常表示为数组。

• 根元素将位于Arr[0]。
• 下表显示了i的其他节点的索引 ^th 节点，即Arr[i]：
  

  Arr[（i-1）/2]	返回父节点
  Arr[（2*i）+1]	返回左子节点
  Arr[（2*i）+2]	返回正确的子节点

  用于实现数组表示的遍历方法是 水平顺序

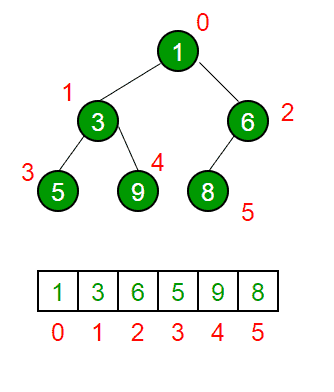
  请参考 二进制堆的数组表示 详细信息。

  堆的应用： 1) 堆排序 ：Heap Sort使用二进制堆在O（nLogn）时间内对数组进行排序。

  2) 优先级队列：使用二进制堆可以有效地实现优先级队列，因为它支持在O（logn）时间内执行insert（）、delete（）和extractmax（）、decreaseKey（）操作。二进制堆和斐波那契堆是二进制堆的变体。这些变体也能有效地执行联合。

  3) 图算法：优先级队列特别用于图算法，如 Dijkstra的最短路径 和 普里姆最小生成树 .

  4) 使用堆可以有效地解决许多问题。例如，见下文。 （a） 数组中第K个最大元素 . b） 对几乎排序的数组进行排序/ c） 合并K排序数组 .

  最小堆上的操作： 1) getMini（）：它返回Min Heap的根元素。该操作的时间复杂度为O（1）。

  2) extractMin（）：从MinHeap中删除最小元素。此操作的时间复杂度为O（Logn），因为此操作需要在删除根后（通过调用heapify（））维护heap属性。

  3) decreaseKey（）：减少键的值。该操作的时间复杂度为O（Logn）。如果一个节点的reduces键值大于该节点的父节点，那么我们不需要做任何事情。否则，我们需要遍历up来修复违反的heap属性。

  4) insert（）：插入新密钥需要O（Logn）时间。我们在树的末尾添加一个新键。如果新密钥大于其父密钥，则无需执行任何操作。否则，我们需要遍历up来修复违反的heap属性。

  5) delete（）：删除密钥也需要O（Logn）时间。我们通过调用decreaseKey（）将要删除的密钥替换为minum infinite。在decreaseKey（）之后，负无穷大的值必须到达根，所以我们调用extractMin（）来移除该键。

  下面是基本堆操作的实现。

  C++

  // A C++ program to demonstrate common Binary Heap Operations #include<iostream> #include<climits> using namespace std; // Prototype of a utility function to swap two integers void swap( int *x, int *y); // A class for Min Heap class MinHeap { int *harr; // pointer to array of elements in heap int capacity; // maximum possible size of min heap int heap_size; // Current number of elements in min heap public : // Constructor MinHeap( int capacity); // to heapify a subtree with the root at given index void MinHeapify( int ); int parent( int i) { return (i-1)/2; } // to get index of left child of node at index i int left( int i) { return (2*i + 1); } // to get index of right child of node at index i int right( int i) { return (2*i + 2); } // to extract the root which is the minimum element int extractMin(); // Decreases key value of key at index i to new_val void decreaseKey( int i, int new_val); // Returns the minimum key (key at root) from min heap int getMin() { return harr[0]; } // Deletes a key stored at index i void deleteKey( int i); // Inserts a new key 'k' void insertKey( int k); }; // Constructor: Builds a heap from a given array a[] of given size MinHeap::MinHeap( int cap) { heap_size = 0; capacity = cap; harr = new int [cap]; } // Inserts a new key 'k' void MinHeap::insertKey( int k) { if (heap_size == capacity) { cout << "Overflow: Could not insertKey" ; return ; } // First insert the new key at the end heap_size++; int i = heap_size - 1; harr[i] = k; // Fix the min heap property if it is violated while (i != 0 && harr[parent(i)] > harr[i]) { swap(&harr[i], &harr[parent(i)]); i = parent(i); } } // Decreases value of key at index 'i' to new_val.  It is assumed that // new_val is smaller than harr[i]. void MinHeap::decreaseKey( int i, int new_val) { harr[i] = new_val; while (i != 0 && harr[parent(i)] > harr[i]) { swap(&harr[i], &harr[parent(i)]); i = parent(i); } } // Method to remove minimum element (or root) from min heap int MinHeap::extractMin() { if (heap_size <= 0) return INT_MAX; if (heap_size == 1) { heap_size--; return harr[0]; } // Store the minimum value, and remove it from heap int root = harr[0]; harr[0] = harr[heap_size-1]; heap_size--; MinHeapify(0); return root; } // This function deletes key at index i. It first reduced value to minus // infinite, then calls extractMin() void MinHeap::deleteKey( int i) { decreaseKey(i, INT_MIN); extractMin(); } // A recursive method to heapify a subtree with the root at given index // This method assumes that the subtrees are already heapified void MinHeap::MinHeapify( int i) { int l = left(i); int r = right(i); int smallest = i; if (l < heap_size && harr[l] < harr[i]) smallest = l; if (r < heap_size && harr[r] < harr[smallest]) smallest = r; if (smallest != i) { swap(&harr[i], &harr[smallest]); MinHeapify(smallest); } } // A utility function to swap two elements void swap( int *x, int *y) { int temp = *x; *x = *y; *y = temp; } // Driver program to test above functions int main() { MinHeap h(11); h.insertKey(3); h.insertKey(2); h.deleteKey(1); h.insertKey(15); h.insertKey(5); h.insertKey(4); h.insertKey(45); cout << h.extractMin() << " " ; cout << h.getMin() << " " ; h.decreaseKey(2, 1); cout << h.getMin(); return 0; }

  python

  # A Python program to demonstrate common binary heap operations # Import the heap functions from python library from heapq import heappush, heappop, heapify # heappop - pop and return the smallest element from heap # heappush - push the value item onto the heap, maintaining #             heap invarient # heapify - transform list into heap, in place, in linear time # A class for Min Heap class MinHeap: # Constructor to initialize a heap def __init__( self ): self .heap = [] def parent( self , i): return (i - 1 ) / 2 # Inserts a new key 'k' def insertKey( self , k): heappush( self .heap, k) # Decrease value of key at index 'i' to new_val # It is assumed that new_val is smaller than heap[i] def decreaseKey( self , i, new_val): self .heap[i] = new_val while (i ! = 0 and self .heap[ self .parent(i)] > self .heap[i]): # Swap heap[i] with heap[parent(i)] self .heap[i] , self .heap[ self .parent(i)] = ( self .heap[ self .parent(i)], self .heap[i]) # Method to remove minium element from min heap def extractMin( self ): return heappop( self .heap) # This functon deletes key at index i. It first reduces # value to minus infinite and then calls extractMin() def deleteKey( self , i): self .decreaseKey(i, float ( "-inf" )) self .extractMin() # Get the minimum element from the heap def getMin( self ): return self .heap[ 0 ] # Driver pgoratm to test above function heapObj = MinHeap() heapObj.insertKey( 3 ) heapObj.insertKey( 2 ) heapObj.deleteKey( 1 ) heapObj.insertKey( 15 ) heapObj.insertKey( 5 ) heapObj.insertKey( 4 ) heapObj.insertKey( 45 ) print heapObj.extractMin(), print heapObj.getMin(), heapObj.decreaseKey( 2 , 1 ) print heapObj.getMin() # This code is contributed by Nikhil Kumar Singh(nickzuck_007)

  C#

  // C# program to demonstrate common // Binary Heap Operations - Min Heap using System; // A class for Min Heap class MinHeap{ // To store array of elements in heap public int [] heapArray{ get ; set ; } // max size of the heap public int capacity{ get ; set ; } // Current number of elements in the heap public int current_heap_size{ get ; set ; } // Constructor public MinHeap( int n) { capacity = n; heapArray = new int [capacity]; current_heap_size = 0; } // Swapping using reference public static void Swap<T>( ref T lhs, ref T rhs) { T temp = lhs; lhs = rhs; rhs = temp; } // Get the Parent index for the given index public int Parent( int key) { return (key - 1) / 2; } // Get the Left Child index for the given index public int Left( int key) { return 2 * key + 1; } // Get the Right Child index for the given index public int Right( int key) { return 2 * key + 2; } // Inserts a new key public bool insertKey( int key) { if (current_heap_size == capacity) { // heap is full return false ; } // First insert the new key at the end int i = current_heap_size; heapArray[i] = key; current_heap_size++; // Fix the min heap property if it is violated while (i != 0 && heapArray[i] < heapArray[Parent(i)]) { Swap( ref heapArray[i], ref heapArray[Parent(i)]); i = Parent(i); } return true ; } // Decreases value of given key to new_val. // It is assumed that new_val is smaller // than heapArray[key]. public void decreaseKey( int key, int new_val) { heapArray[key] = new_val; while (key != 0 && heapArray[key] < heapArray[Parent(key)]) { Swap( ref heapArray[key], ref heapArray[Parent(key)]); key = Parent(key); } } // Returns the minimum key (key at // root) from min heap public int getMin() { return heapArray[0]; } // Method to remove minimum element // (or root) from min heap public int extractMin() { if (current_heap_size <= 0) { return int .MaxValue; } if (current_heap_size == 1) { current_heap_size--; return heapArray[0]; } // Store the minimum value, // and remove it from heap int root = heapArray[0]; heapArray[0] = heapArray[current_heap_size - 1]; current_heap_size--; MinHeapify(0); return root; } // This function deletes key at the // given index. It first reduced value // to minus infinite, then calls extractMin() public void deleteKey( int key) { decreaseKey(key, int .MinValue); extractMin(); } // A recursive method to heapify a subtree // with the root at given index // This method assumes that the subtrees // are already heapified public void MinHeapify( int key) { int l = Left(key); int r = Right(key); int smallest = key; if (l < current_heap_size && heapArray[l] < heapArray[smallest]) { smallest = l; } if (r < current_heap_size && heapArray[r] < heapArray[smallest]) { smallest = r; } if (smallest != key) { Swap( ref heapArray[key], ref heapArray[smallest]); MinHeapify(smallest); } } // Increases value of given key to new_val. // It is assumed that new_val is greater // than heapArray[key]. // Heapify from the given key public void increaseKey( int key, int new_val) { heapArray[key] = new_val; MinHeapify(key); } // Changes value on a key public void changeValueOnAKey( int key, int new_val) { if (heapArray[key] == new_val) { return ; } if (heapArray[key] < new_val) { increaseKey(key, new_val); } else { decreaseKey(key, new_val); } } } static class MinHeapTest{ // Driver code public static void Main( string [] args) { MinHeap h = new MinHeap(11); h.insertKey(3); h.insertKey(2); h.deleteKey(1); h.insertKey(15); h.insertKey(5); h.insertKey(4); h.insertKey(45); Console.Write(h.extractMin() + " " ); Console.Write(h.getMin() + " " ); h.decreaseKey(2, 1); Console.Write(h.getMin()); } } // This code is contributed by // Dinesh Clinton Albert(dineshclinton)

  输出：

  2 4 1

  堆上的编码实践 堆上的所有文章 堆上测验 PriorityQueue:Java库中的二进制堆实现

  如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请写下评论。