语境无关语法和语境无关语言中的歧义

先决条件—— 下推自动机 和 上下文无关语言 .

假设我们有一个上下文无关的语法G和产生式规则：S->aSb | bSa | SS|ℇ

最左边的派生（LMD）和派生树： 从起始符号S到字符串的最左端派生是通过用相应产生式规则的RHS替换最左端的非终止符号来完成的。例如：上面语法G中字符串abab最左边的派生如下：

 S => aSb => abSab => abab

使用产生式规则替换带下划线的符号。

派生树： 它说明了如何使用S中的产生式规则派生字符串，如图1所示。

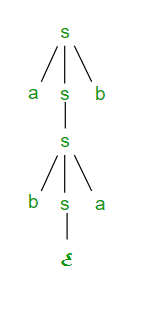
图1

最右边的推导（RMD）： 通过用相应产生式规则的RHS替换最右边的非终结符，从起始符号S派生字符串。例如：上面语法G中最右边的字符串abab派生如下：

S => SS => SaSb => Sab => aSbab => abab

使用产生式规则替换带下划线的符号。使用最右边派生的abab派生树如图2所示。

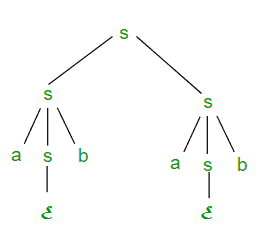
图2

派生可以是LMD或RMD，也可以同时是LMD或RMD，也可以不派生。例如：

S => aSb => abSab => abab is LMD as well as RMDbut S => SS => SaSb => Sab => aSbab => abab is RMD but not LMD.

歧义上下文无关语法： 如果由语法生成的字符串存在多个LMD或多个RMD，则称上下文无关语法为“不明确”。对于歧义语法中的字符串，也将有多个派生树。上面描述的语法是不明确的，因为有两个派生树（图1和图2）。字符串abab可以有多个RMD，它们是：

S => SS => SaSb => Sab => aSbab => ababS => aSb => abSab => abab

不明确的上下文无关语言： 如果没有明确的语法来定义一种与上下文无关的语言，那么它就被称为模糊语言，也被称为固有的模糊上下文无关语言。

注：

• 如果上下文无关语法G是歧义的，那么由语法L（G）生成的语言可能是歧义的，也可能不是歧义的
• 并非总是可以将不明确的CFG转换为明确的CFG。只有一些不明确的CFG可以转换为明确的CFG。
• 目前还没有将模糊CFG转换为明确CFG的算法。
• 总是存在一个明确的CFG对应于明确的CFL。
• 确定性CFL总是毫不含糊的。

问题: 考虑上下文无关文法的下列语句

G = {S->SS, S->ab, S->ba, S->ℇ}

• 我 G是模棱两可的
• 二、 G生成a和b数量相等的所有字符串
• 三、 G可以被确定性PDA接受

下面哪个组合表达了关于G的所有真实陈述？

1. 我只是
2. 只有我和我
3. 仅限II和III
4. 一、 二、三

解决方案： 对于字符串abab有不同的LMD，可以

S => SS => SSS => abSS => ababS => ababS => SS => abS => abab

所以语法是模棱两可的。所以我说的是真的。

语句II说明语法G生成所有a和b数量相等的字符串，但它不能生成aabb字符串。因此，声明二是不正确的。

报表三也是正确的，因为它可以被客户接受。所以正确的选择是（B）。

问题: 以下哪项陈述是错误的？

1. 存在上下文无关语言，因此生成它们的所有上下文无关语法都是模糊的。
2. 一个明确的上下文无关语法对于它生成的每一个语言字符串都有一个唯一的解析树。
3. 确定性和非确定性下推自动机总是接受同一组语言。
4. 一个字母表中的有限字符串集始终是一种规则语言。

解决方案： （A） 因为所有的CFL都是不明确的。

（B） 这也是正确的，因为毫不含糊的CFG为其生成的每个语言字符串都有一个唯一的解析树。

（C） 是错误的，因为一些语言被非确定性PDA接受，但不被确定性PDA接受。

（D） 这也是事实，因为字符串的有限集总是正则的。

所以选项（C）是正确的选项。

本文由 奏鸣曲。 如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请写评论