函数依赖的等价性

为了理解函数依赖集（FD集）的等价性，在 这 文章

给定一个具有不同FD集的关系，我们必须找出一个FD集是另一个FD集的子集还是两者相等。

如何找到两个FD集合之间的关系？

设FD1和FD2是关系R的两个FD集。

1. 如果FD1的所有FD都可以从FD2中存在的FD派生出来，我们可以说FD2⊃ FD1。
2. 如果FD2的所有FD都可以从FD1中存在的FD派生出来，我们可以说FD1⊃ FD2。
3. 如果1和2都为真，则FD1=FD2。

所有这三种情况都可以使用维恩图显示为：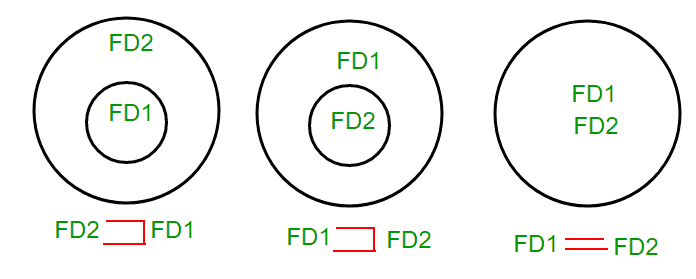

问：让我们举一个例子来说明两个FD集之间的关系。具有两个FD集FD1={A->B，B->C，AB->D}和FD2={A->B，B->C，A->C，A->D}的关系R（A，B，C，D）

第一步。 检查FD1的所有FD是否都存在于FD2中

• 集合FD1中的A->B存在于集合FD2中。
• 集合FD1中的B->C也存在于集合FD2中。
• AB->D在集合FD1中存在，但在FD2中不直接存在，但我们将检查是否可以导出它。对于集合FD2（AB） ⁺ ={A，B，C，D}。这意味着AB可以在功能上确定A、B、C和D。因此AB->D也将在集合FD2中保持不变。

由于集合FD1中的所有FD也保留在集合FD2中，所以FD2⊃ FD1是真的。

第二步。 检查FD1中是否存在FD2的所有FD

• 集合FD2中的A->B出现在集合FD1中。
• 集合FD2中的B->C也存在于集合FD1中。
• A->C存在于FD2中，但不直接存在于FD1中，但我们将检查是否可以导出它。对于集合FD1（A） ⁺ ={A，B，C，D}。这意味着A可以在功能上决定A、B、C和D。因此A->C也将在集合FD1中保持。
• A->D存在于FD2中，但不直接存在于FD1中，但我们将检查是否可以导出它。对于集合FD1（A） ⁺ ={A，B，C，D}。这意味着A可以在功能上决定A、B、C和D。因此A->D也将在集合FD1中保持。

由于集合FD2中的所有FD也保留在集合FD1中，所以FD1⊃ FD2是真的。

第三步。 作为FD2⊃ FD1和FD1⊃ FD2均为真FD2=FD1为真。这两个FD集在语义上是等价的。

问：让我们再举一个例子来说明两个FD集之间的关系。具有两个FD集FD1={A->B，B->C，A->C}和FD2={A->B，B->C，A->D}的关系R2（A，B，C，D）

第一步。 检查FD1的所有FD是否都存在于FD2中

• 集合FD1中的A->B存在于集合FD2中。
• 集合FD1中的B->C也存在于集合FD2中。
• A->C存在于FD1中，但不直接存在于FD2中，但我们将检查是否可以导出它。对于集合FD2（A） ⁺ ={A，B，C，D}。这意味着A可以在功能上决定A、B、C和D。因此A->C也将在集合FD2中保持不变。

由于集合FD1中的所有FD也保留在集合FD2中，所以FD2⊃ FD1是真的。

第二步。 检查FD1中是否存在FD2的所有FD

• 集合FD2中的A->B出现在集合FD1中。
• 集合FD2中的B->C也存在于集合FD1中。
• A->D存在于FD2中，但不直接存在于FD1中，但我们将检查是否可以导出它。对于集合FD1（A） ⁺ ={A，B，C}。这意味着A不能从功能上确定D。所以A->D在FD1中不起作用。

由于集合FD2中的所有FD不在集合FD1中保持不变，因此FD2⊄ FD1。

第三步。 在本例中，FD2⊃ FD1和FD2⊄ FD1，这两个FD集合在语义上是不等价的。

本文由Sonal Tuteja撰稿。如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请写评论。