选择排序-yiteyi-C++库

选择排序算法通过从未排序的部分重复查找最小元素（考虑升序）并将其放在开头来对数组进行排序。该算法在给定的数组中保留两个子数组。 1）已排序的子数组。 2）未排序的剩余子阵列。在选择排序的每次迭代中，从未排序的子数组中选取最小元素（考虑升序），并将其移动到已排序的子数组中。以下示例解释了上述步骤：

null

arr[] = 64 25 12 22 11

// Find the minimum element in arr[0...4]
// and place it at beginning
11 25 12 22 64

// Find the minimum element in arr[1...4]
// and place it at beginning of arr[1...4]
11 12 25 22 64

// Find the minimum element in arr[2...4]
// and place it at beginning of arr[2...4]
11 12 22 25 64

// Find the minimum element in arr[3...4]
// and place it at beginning of arr[3...4]
11 12 22 25 64

选择排序的流程图：

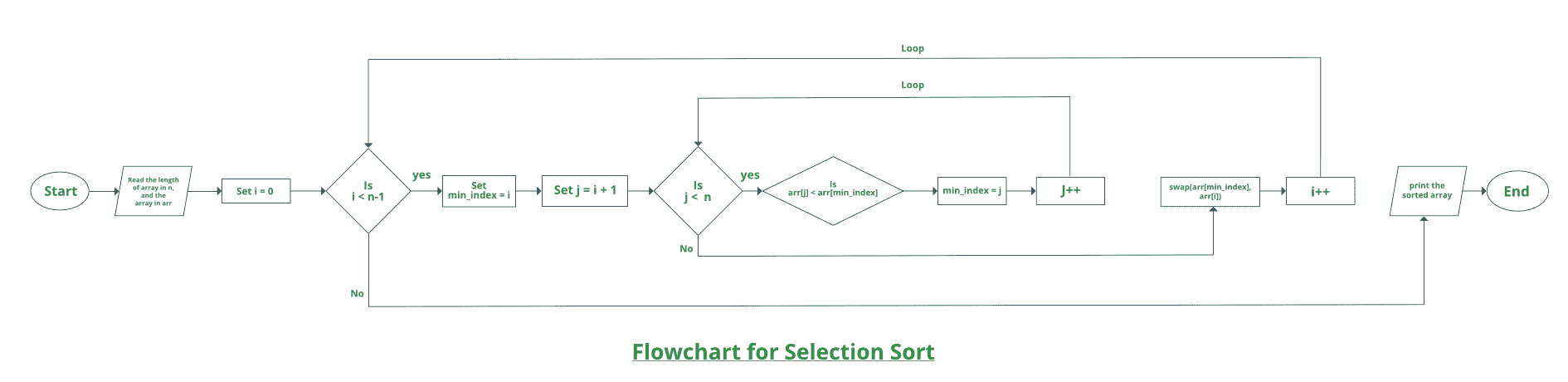
Selection-Sort-Flowhchart

建议：请在“上解决” 实践 “首先，在讨论解决方案之前。

C++

                         // C++ program for implementation of selection sort                       
                         #include <bits/stdc++.h>                       
                         using                                     namespace                                     std;                       
                                   
                         void                                     swap(                                     int                                     *xp,                                     int                                     *yp)                       
                         {                       
                                                 int                                     temp = *xp;                       
                                                 *xp = *yp;                       
                                                 *yp = temp;                       
                         }                       
                                   
                         void                                     selectionSort(                                     int                                     arr[],                                     int                                     n)                       
                         {                       
                                                 int                                     i, j, min_idx;                       
                                   
                                                 // One by one move boundary of unsorted subarray                       
                                                 for                                     (i = 0; i < n-1; i++)                       
                                                 {                       
                                                 // Find the minimum element in unsorted array                       
                                                 min_idx = i;                       
                                                 for                                     (j = i+1; j < n; j++)                       
                                                 if                                     (arr[j] < arr[min_idx])                       
                                                 min_idx = j;                       
                                   
                                                 // Swap the found minimum element with the first element                       
                                                 swap(&arr[min_idx], &arr[i]);                       
                                                 }                       
                         }                       
                                   
                         /* Function to print an array */                       
                         void                                     printArray(                                     int                                     arr[],                                     int                                     size)                       
                         {                       
                                                 int                                     i;                       
                                                 for                                     (i=0; i < size; i++)                       
                                                 cout << arr[i] <<                                     " "                                     ;                       
                                                 cout << endl;                       
                         }                       
                                   
                         // Driver program to test above functions                       
                         int                                     main()                       
                         {                       
                                                 int                                     arr[] = {64, 25, 12, 22, 11};                       
                                                 int                                     n =                                     sizeof                                     (arr)/                                     sizeof                                     (arr[0]);                       
                                                 selectionSort(arr, n);                       
                                                 cout <<                                     "Sorted array: "                                     ;                       
                                                 printArray(arr, n);                       
                                                 return                                     0;                       
                         }                       
                                   
                         // This is code is contributed by rathbhupendra                       

C

                         // C program for implementation of selection sort                       
                         #include <stdio.h>                       
                                   
                         void                                     swap(                                     int                                     *xp,                                     int                                     *yp)                       
                         {                       
                                                 int                                     temp = *xp;                       
                                                 *xp = *yp;                       
                                                 *yp = temp;                       
                         }                       
                                   
                         void                                     selectionSort(                                     int                                     arr[],                                     int                                     n)                       
                         {                       
                                                 int                                     i, j, min_idx;                       
                                   
                                                 // One by one move boundary of unsorted subarray                       
                                                 for                                     (i = 0; i < n-1; i++)                       
                                                 {                       
                                                 // Find the minimum element in unsorted array                       
                                                 min_idx = i;                       
                                                 for                                     (j = i+1; j < n; j++)                       
                                                 if                                     (arr[j] < arr[min_idx])                       
                                                 min_idx = j;                       
                                   
                                                 // Swap the found minimum element with the first element                       
                                                 swap(&arr[min_idx], &arr[i]);                       
                                                 }                       
                         }                       
                                   
                         /* Function to print an array */                       
                         void                                     printArray(                                     int                                     arr[],                                     int                                     size)                       
                         {                       
                                                 int                                     i;                       
                                                 for                                     (i=0; i < size; i++)                       
                                                 printf                                     (                                     "%d "                                     , arr[i]);                       
                                                 printf                                     (                                     ""                                     );                       
                         }                       
                                   
                         // Driver program to test above functions                       
                         int                                     main()                       
                         {                       
                                                 int                                     arr[] = {64, 25, 12, 22, 11};                       
                                                 int                                     n =                                     sizeof                                     (arr)/                                     sizeof                                     (arr[0]);                       
                                                 selectionSort(arr, n);                       
                                                 printf                                     (                                     "Sorted array: "                                     );                       
                                                 printArray(arr, n);                       
                                                 return                                     0;                       
                         }                       

Python3

                         # Python program for implementation of Selection                       
                         # Sort                       
                         import                                     sys                       
                         A                                     =                                     [                                     64                                     ,                                     25                                     ,                                     12                                     ,                                     22                                     ,                                     11                                     ]                       
                                   
                         # Traverse through all array elements                       
                         for                                     i                                     in                                     range                                     (                                     len                                     (A)):                       
                                   
                                                 # Find the minimum element in remaining                       
                                                 # unsorted array                       
                                                 min_idx                                     =                                     i                       
                                                 for                                     j                                     in                                     range                                     (i                                     +                                     1                                     ,                                     len                                     (A)):                       
                                                 if                                     A[min_idx] > A[j]:                       
                                                 min_idx                                     =                                     j                       
                                   
                                                 # Swap the found minimum element with                       
                                                 # the first element                       
                                                 A[i], A[min_idx]                                     =                                     A[min_idx], A[i]                       
                                   
                         # Driver code to test above                       
                         print                                     (                                     "Sorted array"                                     )                       
                         for                                     i                                     in                                     range                                     (                                     len                                     (A)):                       
                                                 print                                     (                                     "%d"                                     %                                     A[i],end                                     =                                     " "                                     )                       

JAVA

                         // Java program for implementation of Selection Sort                       
                         class                                     SelectionSort                       
                         {                       
                                                 void                                     sort(                                     int                                     arr[])                       
                                                 {                       
                                                 int                                     n = arr.length;                       
                                   
                                                 // One by one move boundary of unsorted subarray                       
                                                 for                                     (                                     int                                     i =                                     0                                     ; i < n-                                     1                                     ; i++)                       
                                                 {                       
                                                 // Find the minimum element in unsorted array                       
                                                 int                                     min_idx = i;                       
                                                 for                                     (                                     int                                     j = i+                                     1                                     ; j < n; j++)                       
                                                 if                                     (arr[j] < arr[min_idx])                       
                                                 min_idx = j;                       
                                   
                                                 // Swap the found minimum element with the first                       
                                                 // element                       
                                                 int                                     temp = arr[min_idx];                       
                                                 arr[min_idx] = arr[i];                       
                                                 arr[i] = temp;                       
                                                 }                       
                                                 }                       
                                   
                                                 // Prints the array                       
                                                 void                                     printArray(                                     int                                     arr[])                       
                                                 {                       
                                                 int                                     n = arr.length;                       
                                                 for                                     (                                     int                                     i=                                     0                                     ; i<n; ++i)                       
                                                 System.out.print(arr[i]+                                     " "                                     );                       
                                                 System.out.println();                       
                                                 }                       
                                   
                                                 // Driver code to test above                       
                                                 public                                     static                                     void                                     main(String args[])                       
                                                 {                       
                                                 SelectionSort ob =                                     new                                     SelectionSort();                       
                                                 int                                     arr[] = {                                     64                                     ,                                     25                                     ,                                     12                                     ,                                     22                                     ,                                     11                                     };                       
                                                 ob.sort(arr);                       
                                                 System.out.println(                                     "Sorted array"                                     );                       
                                                 ob.printArray(arr);                       
                                                 }                       
                         }                       
                         /* This code is contributed by Rajat Mishra*/                       

C#

                         // C# program for implementation                       
                         // of Selection Sort                       
                         using                                     System;                       
                                   
                         class                                     GFG                       
                         {                       
                                                 static                                     void                                     sort(                                     int                                     []arr)                       
                                                 {                       
                                                 int                                     n = arr.Length;                       
                                   
                                                 // One by one move boundary of unsorted subarray                       
                                                 for                                     (                                     int                                     i = 0; i < n - 1; i++)                       
                                                 {                       
                                                 // Find the minimum element in unsorted array                       
                                                 int                                     min_idx = i;                       
                                                 for                                     (                                     int                                     j = i + 1; j < n; j++)                       
                                                 if                                     (arr[j] < arr[min_idx])                       
                                                 min_idx = j;                       
                                   
                                                 // Swap the found minimum element with the first                       
                                                 // element                       
                                                 int                                     temp = arr[min_idx];                       
                                                 arr[min_idx] = arr[i];                       
                                                 arr[i] = temp;                       
                                                 }                       
                                                 }                       
                                   
                                                 // Prints the array                       
                                                 static                                     void                                     printArray(                                     int                                     []arr)                       
                                                 {                       
                                                 int                                     n = arr.Length;                       
                                                 for                                     (                                     int                                     i=0; i<n; ++i)                       
                                                 Console.Write(arr[i]+                                     " "                                     );                       
                                                 Console.WriteLine();                       
                                                 }                       
                                   
                                                 // Driver code                       
                                                 public                                     static                                     void                                     Main()                       
                                                 {                       
                                                 int                                     []arr = {64,25,12,22,11};                       
                                                 sort(arr);                       
                                                 Console.WriteLine(                                     "Sorted array"                                     );                       
                                                 printArray(arr);                       
                                                 }                       
                                   
                         }                       
                         // This code is contributed by Sam007                       

PHP

                         <?php                       
                         // PHP program for implementation                       
                         // of selection sort                       
                         function                                     selection_sort(&                                     $arr                                     ,                                     $n                                     )                       
                         {                       
                                                 for                                     (                                     $i                                     = 0;                                     $i                                     <                                     $n                                     ;                                     $i                                     ++)                       
                                                 {                       
                                                 $low                                     =                                     $i                                     ;                       
                                                 for                                     (                                     $j                                     =                                     $i                                     + 1;                                     $j                                     <                                     $n                                     ;                                     $j                                     ++)                       
                                                 {                       
                                                 if                                     (                                     $arr                                     [                                     $j                                     ] <                                     $arr                                     [                                     $low                                     ])                       
                                                 {                       
                                                 $low                                     =                                     $j                                     ;                       
                                                 }                       
                                                 }                       
                                   
                                                 // swap the minimum value to $ith node                       
                                                 if                                     (                                     $arr                                     [                                     $i                                     ] >                                     $arr                                     [                                     $low                                     ])                       
                                                 {                       
                                                 $tmp                                     =                                     $arr                                     [                                     $i                                     ];                       
                                                 $arr                                     [                                     $i                                     ] =                                     $arr                                     [                                     $low                                     ];                       
                                                 $arr                                     [                                     $low                                     ] =                                     $tmp                                     ;                       
                                                 }                       
                                                 }                       
                         }                       
                                   
                         // Driver Code                       
                         $arr                                     =                                     array                                     (64, 25, 12, 22, 11);                       
                         $len                                     =                                     count                                     (                                     $arr                                     );                       
                         selection_sort(                                     $arr                                     ,                                     $len                                     );                       
                         echo                                     "Sorted array : "                                     ;                       
                                   
                         for                                     (                                     $i                                     = 0;                                     $i                                     <                                     $len                                     ;                                     $i                                     ++)                       
                                                 echo                                     $arr                                     [                                     $i                                     ] .                                     " "                                     ;                       
                                   
                         // This code is contributed                       
                         // by Deepika Gupta.                       
                         ?>                       

Javascript

                         <script>                       
                         // Javascript program for implementation of selection sort                       
                         function                                     swap(arr,xp, yp)                       
                         {                       
                                                 var                                     temp = arr[xp];                       
                                                 arr[xp] = arr[yp];                       
                                                 arr[yp] = temp;                       
                         }                       
                                   
                         function                                     selectionSort(arr,  n)                       
                         {                       
                                                 var                                     i, j, min_idx;                       
                                   
                                                 // One by one move boundary of unsorted subarray                       
                                                 for                                     (i = 0; i < n-1; i++)                       
                                                 {                       
                                                 // Find the minimum element in unsorted array                       
                                                 min_idx = i;                       
                                                 for                                     (j = i + 1; j < n; j++)                       
                                                 if                                     (arr[j] < arr[min_idx])                       
                                                 min_idx = j;                       
                                   
                                                 // Swap the found minimum element with the first element                       
                                                 swap(arr,min_idx, i);                       
                                                 }                       
                         }                       
                                   
                         function                                     printArray( arr,  size)                       
                         {                       
                                                 var                                     i;                       
                                                 for                                     (i = 0; i < size; i++)                       
                                                 document.write(arr[i] +                                     " "                                     );                       
                                                 document.write(                                     " <br>"                                     );                       
                         }                       
                                   
                         var                                     arr = [64, 25, 12, 22, 11];                       
                                                 var                                     n = 5;                       
                                                 selectionSort(arr, n);                       
                                                 document.write(                                     "Sorted array: <br>"                                     );                       
                                                 printArray(arr, n);                       
                                   
                         // This code is contributed by akshitsaxenaa09.                       
                         </script>                       

输出：

Sorted array: 
11 12 22 25 64

时间复杂性： O（n） ^2. )因为有两个嵌套循环。 辅助空间： O（1）选择排序的好处在于，它不会进行超过O（n）次的交换，并且在内存写入是一项代价高昂的操作时非常有用。 练习： 使用选择排序对字符串数组进行排序稳定性：默认实现不稳定。然而，它可以变得稳定。请看稳定选择排序详细信息。 到位： 是的，它不需要额外的空间。

快照： 选择排序测验 Geeksforgeks/Geeksquick上的其他排序算法： 分类编码实践。如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请写评论

文章版权归作者所有，未经允许请勿转载。

THE END

技术文章