当我们有可能具有重复键的键值对时(比如人名作为键,他们的细节作为值),稳定性主要很重要。我们希望按键对这些对象进行排序。
这是怎么一回事? 如果两个具有相等键的对象在排序输出中的顺序与它们在待排序的输入数组中的顺序相同,则称排序算法是稳定的。
从形式上讲,稳定性可以定义为:, 让 ![]() 做一个数组,让
做一个数组,让 ![]() 在元素上是严格的弱序
在元素上是严格的弱序 ![]() . 排序算法是稳定的,如果-
. 排序算法是稳定的,如果- ![]() 哪里
哪里 ![]() 是排序排列(排序移动)
是排序排列(排序移动) ![]() 定位
定位 ![]() ) 非正式地说,稳定性意味着对等元素在排序后保留其相对位置。
) 非正式地说,稳定性意味着对等元素在排序后保留其相对位置。
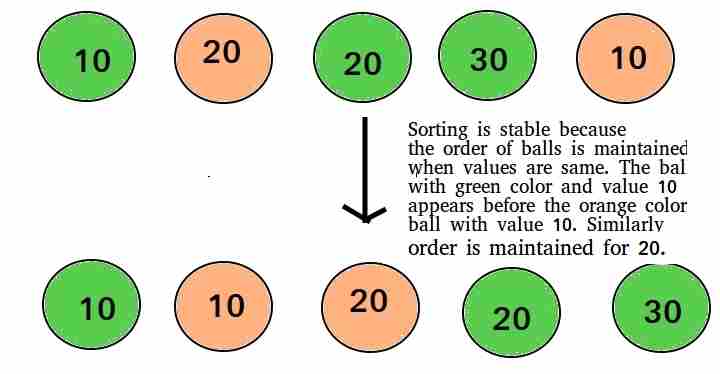
我们关心像整数数组这样的简单数组吗? 当相等的元素不可区分时,比如整数,或者更一般地说,任何以整个元素为关键的数据,稳定性不是问题。如果所有钥匙都不同,稳定性也不是问题。
这是一个有用的例子 考虑下面的学生姓名数据集及其相应的类节。

如果我们只根据名称对这些数据进行排序,那么生成的数据集也不太可能按照部分进行分组。

因此,我们可能需要再次排序,以获得学生名单的部分。但是这样做的时候,如果排序算法不稳定,我们可能会得到这样的结果-

数据集现在是按节排序的,但不是按名称排序的。 在名称排序数据集中,元组 ![]() 以前
以前 ![]() ,但由于排序算法不稳定,相对顺序丢失。 另一方面,如果我们使用稳定的排序算法,结果会是-
,但由于排序算法不稳定,相对顺序丢失。 另一方面,如果我们使用稳定的排序算法,结果会是-
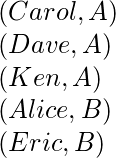
在这里,不同元组之间的相对顺序保持不变。在这种情况下,相对顺序可能会保持在不稳定的排序中,但这是极不可能的。
哪些排序算法是稳定的? 有些排序算法本质上是稳定的,例如 气泡排序 , 插入排序 , 合并排序 , 计数排序 等 基于比较的稳定排序,如合并排序和插入排序,通过确保- 要素 ![]() 先于
先于 ![]() 如果且仅当
如果且仅当 ![]() 这里i,j是指数和
这里i,j是指数和 ![]() . 自从
. 自从 ![]() ,相对顺序得以保留
,相对顺序得以保留 ![]() 即
即 ![]() 先于
先于 ![]() . 其他非基于比较的分类,如 计数排序 通过确保按相反顺序填充排序的数组来保持稳定性,以便具有等效键的元素具有相同的相对位置。 比如 基数排序 依赖于另一类,唯一的要求是另一类应该是稳定的。
. 其他非基于比较的分类,如 计数排序 通过确保按相反顺序填充排序的数组来保持稳定性,以便具有等效键的元素具有相同的相对位置。 比如 基数排序 依赖于另一类,唯一的要求是另一类应该是稳定的。
哪些排序算法不稳定? 快速排序 , 堆排序 等,也可以通过考虑元件的位置使其稳定。这种改变可能不会对性能造成太大影响,也可能会占用一些额外的空间 ![]() .
.
我们能使任何排序算法稳定吗? 任何给定的不稳定排序算法都可以修改为稳定。可以通过特定于排序算法的方法使其稳定,但一般来说,任何本质上不稳定的基于比较的排序算法都可以通过更改键比较操作修改为稳定,以便两个键的比较将位置视为具有相等键的对象的一个因素。
参考资料: http://www.math.uic.edu/~leon/cs-mcs401-s08/讲义/稳定性。pdf http://en.wikipedia.org/wiki/Sorting_algorithm#Stability
本文由 希拉格·曼瓦尼 .如果你喜欢GeekSforgek,并想贡献自己的力量,你也可以使用 贡献极客。组织 或者把你的文章寄到contribute@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上,并帮助其他极客。
如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写下评论。
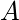


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



