Prerequisite : Segment Tree Persistency in Data Structure
段树本身就是一种很好的数据结构,在很多情况下都会发挥作用。在本文中,我们将介绍此数据结构中的持久性概念。坚持,仅仅意味着保留变化。但很明显,保留这些更改会导致额外的内存消耗,从而影响时间复杂度。
我们的目标是在片段树中应用持久性,并确保不需要超过 O(logn)时间和空间 每改变一次。
让我们从版本的角度来考虑,也就是说,对于片段树中的每个更改,我们都会创建一个新版本。 我们将考虑我们的初始版本是版本0。现在,当我们在段树中进行任何更新时,我们将为其创建一个新版本,并以类似的方式跟踪所有版本的记录。
但是为每个版本创建整个树需要额外的空间和时间。因此,对于大量的版本,这个想法会耗尽时间和内存。
让我们利用这样一个事实:对于段树中的每个新更新(为了简单起见,请说点更新),将修改最大logn节点数。因此,我们的新版本将只包含这些logn新节点,其余节点将与以前的版本相同。因此,很明显,对于每个新版本,我们只需要创建这些logn新节点,而其他节点可以从以前的版本共享。
考虑下面的图以更好的可视化(点击图像以便更好地查看):
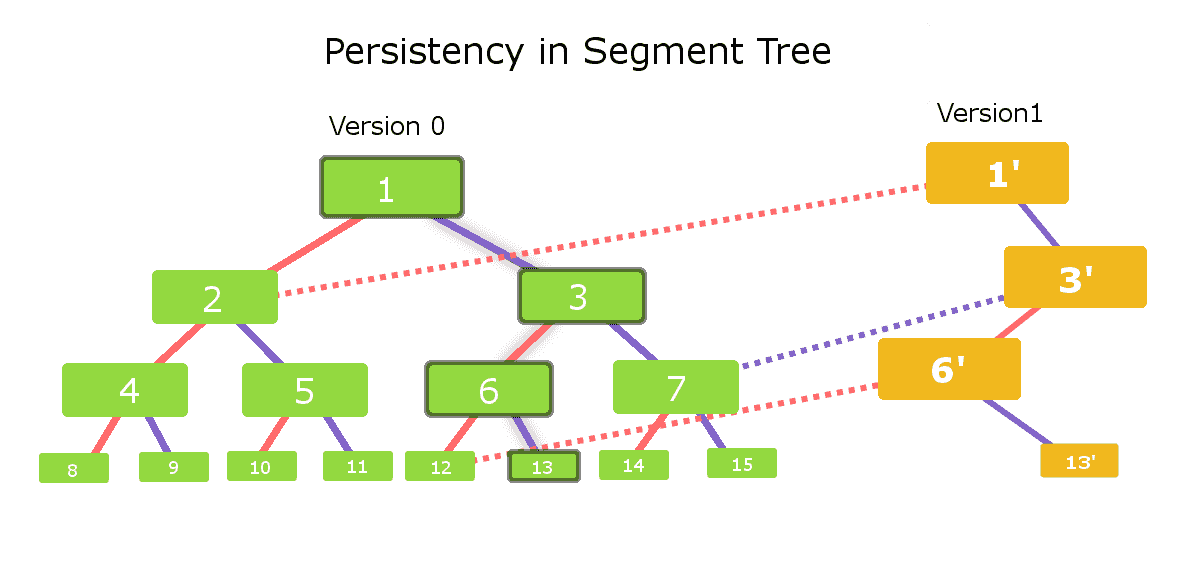
考虑具有绿色节点的段树。我们把这段树称为 版本-0 .每个节点的左子节点与实心红色边连接,而每个节点的右子节点与实心紫色边连接。显然,这段树由15个节点组成。
现在考虑我们需要在版本号13的叶子节点中进行更改。 因此,受影响的节点将—— 节点13、节点6、节点3、节点1 . 因此,对于新版本 (第1版) 我们只需要创造这些 4个新节点 .
现在,让我们为段树中的这一变化构建版本1。我们需要一个新的节点1,因为它受到节点13中所做更改的影响。因此,我们将首先创建一个新的 节点1′ (黄色)。节点1’的左子节点与版本0中节点1的左子节点相同。因此,我们将节点1′的左子节点连接到版本0的节点2(图中的红色虚线)。现在,让我们检查版本1中节点1’的正确子级。我们需要在受影响时创建一个新节点。因此,我们创建了一个名为node 3′的新节点,并使其成为node 1′(实心紫色边连接)的正确子节点。
我们现在将以类似的方式检查 节点3′ .左边的子节点受到影响,因此我们创建了一个名为 节点6′ 并用实心红边将其与节点3′连接,其中作为节点3′的右子节点与版本0中节点3的右子节点相同。因此,我们将使版本0中节点3的右子节点成为版本1中节点3′的右子节点(参见紫色虚线边缘)
对节点6′执行相同的过程,我们看到节点6′的左子节点将是版本0(红色虚线连接)中节点6的左子节点,右子节点是新创建的名为 节点13′ (纯紫色虚线边缘)。 每个 黄色节点 是一个新创建的节点,虚线边是段树的不同版本之间的相互连接。
现在,问题出现了: 如何跟踪所有版本? –我们只需要跟踪所有版本的第一个根节点,这将用于跟踪不同版本中所有新创建的节点。为此,我们可以为所有版本维护指向段树第一个节点的指针数组。
让我们考虑一个非常基本的问题,看看如何在段树中实现持久性。
Problem : Given an array A[] and different point update operations.Considering each point operation to create a new version of the array. We need to answer the queries of typeQ v l r : output the sum of elements in range l to r just after the v-th update.
我们将创建段树的所有版本,并跟踪它们的根节点。然后,对于每个范围和查询,我们将在查询函数中传递所需版本的根节点,并输出所需的和。
以下是针对上述问题的实施:-
C++
// C++ program to implement persistent segment // tree. #include "bits/stdc++.h" using namespace std; #define MAXN 100 /* data type for individual * node in the segment tree */ struct node { // stores sum of the elements in node int val; // pointer to left and right children node* left, *right; // required constructors........ node() {} node(node* l, node* r, int v) { left = l; right = r; val = v; } }; // input array int arr[MAXN]; // root pointers for all versions node* version[MAXN]; // Constructs Version-0 // Time Complexity : O(nlogn) void build(node* n, int low, int high) { if (low==high) { n->val = arr[low]; return ; } int mid = (low+high) / 2; n->left = new node(NULL, NULL, 0); n->right = new node(NULL, NULL, 0); build(n->left, low, mid); build(n->right, mid+1, high); n->val = n->left->val + n->right->val; } /** * Upgrades to new Version * @param prev : points to node of previous version * @param cur : points to node of current version * Time Complexity : O(logn) * Space Complexity : O(logn) */ void upgrade(node* prev, node* cur, int low, int high, int idx, int value) { if (idx > high or idx < low or low > high) return ; if (low == high) { // modification in new version cur->val = value; return ; } int mid = (low+high) / 2; if (idx <= mid) { // link to right child of previous version cur->right = prev->right; // create new node in current version cur->left = new node(NULL, NULL, 0); upgrade(prev->left,cur->left, low, mid, idx, value); } else { // link to left child of previous version cur->left = prev->left; // create new node for current version cur->right = new node(NULL, NULL, 0); upgrade(prev->right, cur->right, mid+1, high, idx, value); } // calculating data for current version // by combining previous version and current // modification cur->val = cur->left->val + cur->right->val; } int query(node* n, int low, int high, int l, int r) { if (l > high or r < low or low > high) return 0; if (l <= low and high <= r) return n->val; int mid = (low+high) / 2; int p1 = query(n->left,low,mid,l,r); int p2 = query(n->right,mid+1,high,l,r); return p1+p2; } int main( int argc, char const *argv[]) { int A[] = {1,2,3,4,5}; int n = sizeof (A)/ sizeof ( int ); for ( int i=0; i<n; i++) arr[i] = A[i]; // creating Version-0 node* root = new node(NULL, NULL, 0); build(root, 0, n-1); // storing root node for version-0 version[0] = root; // upgrading to version-1 version[1] = new node(NULL, NULL, 0); upgrade(version[0], version[1], 0, n-1, 4, 1); // upgrading to version-2 version[2] = new node(NULL, NULL, 0); upgrade(version[1],version[2], 0, n-1, 2, 10); cout << "In version 1 , query(0,4) : " ; cout << query(version[1], 0, n-1, 0, 4) << endl; cout << "In version 2 , query(3,4) : " ; cout << query(version[2], 0, n-1, 3, 4) << endl; cout << "In version 0 , query(0,3) : " ; cout << query(version[0], 0, n-1, 0, 3) << endl; return 0; } |
JAVA
// Java program to implement persistent // segment tree. class GFG{ // Declaring maximum number static Integer MAXN = 100 ; // Making Node for tree static class node { // Stores sum of the elements in node int val; // Reference to left and right children node left, right; // Required constructors.. node() {} // Node constructor for l,r,v node(node l, node r, int v) { left = l; right = r; val = v; } } // Input array static int [] arr = new int [MAXN]; // Root pointers for all versions static node version[] = new node[MAXN]; // Constructs Version-0 // Time Complexity : O(nlogn) static void build(node n, int low, int high) { if (low == high) { n.val = arr[low]; return ; } int mid = (low + high) / 2 ; n.left = new node( null , null , 0 ); n.right = new node( null , null , 0 ); build(n.left, low, mid); build(n.right, mid + 1 , high); n.val = n.left.val + n.right.val; } /* Upgrades to new Version * @param prev : points to node of previous version * @param cur : points to node of current version * Time Complexity : O(logn) * Space Complexity : O(logn) */ static void upgrade(node prev, node cur, int low, int high, int idx, int value) { if (idx > high || idx < low || low > high) return ; if (low == high) { // Modification in new version cur.val = value; return ; } int mid = (low + high) / 2 ; if (idx <= mid) { // Link to right child of previous version cur.right = prev.right; // Create new node in current version cur.left = new node( null , null , 0 ); upgrade(prev.left, cur.left, low, mid, idx, value); } else { // Link to left child of previous version cur.left = prev.left; // Create new node for current version cur.right = new node( null , null , 0 ); upgrade(prev.right, cur.right, mid + 1 , high, idx, value); } // Calculating data for current version // by combining previous version and current // modification cur.val = cur.left.val + cur.right.val; } static int query(node n, int low, int high, int l, int r) { if (l > high || r < low || low > high) return 0 ; if (l <= low && high <= r) return n.val; int mid = (low + high) / 2 ; int p1 = query(n.left, low, mid, l, r); int p2 = query(n.right, mid + 1 , high, l, r); return p1 + p2; } // Driver code public static void main(String[] args) { int A[] = { 1 , 2 , 3 , 4 , 5 }; int n = A.length; for ( int i = 0 ; i < n; i++) arr[i] = A[i]; // Creating Version-0 node root = new node( null , null , 0 ); build(root, 0 , n - 1 ); // Storing root node for version-0 version[ 0 ] = root; // Upgrading to version-1 version[ 1 ] = new node( null , null , 0 ); upgrade(version[ 0 ], version[ 1 ], 0 , n - 1 , 4 , 1 ); // Upgrading to version-2 version[ 2 ] = new node( null , null , 0 ); upgrade(version[ 1 ], version[ 2 ], 0 , n - 1 , 2 , 10 ); // For print System.out.print( "In version 1 , query(0,4) : " ); System.out.print(query(version[ 1 ], 0 , n - 1 , 0 , 4 )); System.out.print( "In version 2 , query(3,4) : " ); System.out.print(query(version[ 2 ], 0 , n - 1 , 3 , 4 )); System.out.print( "In version 0 , query(0,3) : " ); System.out.print(query(version[ 0 ], 0 , n - 1 , 0 , 3 )); } } // This code is contributed by mark_85 |
C#
// C# program to implement persistent // segment tree. using System; class node { // Stores sum of the elements in node public int val; // Reference to left and right children public node left, right; // Required constructors.. public node() {} // Node constructor for l,r,v public node(node l, node r, int v) { left = l; right = r; val = v; } } class GFG{ // Declaring maximum number static int MAXN = 100; // Making Node for tree // Input array static int [] arr = new int [MAXN]; // Root pointers for all versions static node[] version = new node[MAXN]; // Constructs Version-0 // Time Complexity : O(nlogn) static void build(node n, int low, int high) { if (low == high) { n.val = arr[low]; return ; } int mid = (low + high) / 2; n.left = new node( null , null , 0); n.right = new node( null , null , 0); build(n.left, low, mid); build(n.right, mid + 1, high); n.val = n.left.val + n.right.val; } /* Upgrades to new Version * @param prev : points to node of previous version * @param cur : points to node of current version * Time Complexity : O(logn) * Space Complexity : O(logn) */ static void upgrade(node prev, node cur, int low, int high, int idx, int value) { if (idx > high || idx < low || low > high) return ; if (low == high) { // Modification in new version cur.val = value; return ; } int mid = (low + high) / 2; if (idx <= mid) { // Link to right child of previous version cur.right = prev.right; // Create new node in current version cur.left = new node( null , null , 0); upgrade(prev.left, cur.left, low, mid, idx, value); } else { // Link to left child of previous version cur.left = prev.left; // Create new node for current version cur.right = new node( null , null , 0); upgrade(prev.right, cur.right, mid + 1, high, idx, value); } // Calculating data for current version // by combining previous version and current // modification cur.val = cur.left.val + cur.right.val; } static int query(node n, int low, int high, int l, int r) { if (l > high || r < low || low > high) return 0; if (l <= low && high <= r) return n.val; int mid = (low + high) / 2; int p1 = query(n.left, low, mid, l, r); int p2 = query(n.right, mid + 1, high, l, r); return p1 + p2; } // Driver code public static void Main(String[] args) { int [] A = { 1, 2, 3, 4, 5 }; int n = A.Length; for ( int i = 0; i < n; i++) arr[i] = A[i]; // Creating Version-0 node root = new node( null , null , 0); build(root, 0, n - 1); // Storing root node for version-0 version[0] = root; // Upgrading to version-1 version[1] = new node( null , null , 0); upgrade(version[0], version[1], 0, n - 1, 4, 1); // Upgrading to version-2 version[2] = new node( null , null , 0); upgrade(version[1], version[2], 0, n - 1, 2, 10); // For print Console.Write( "In version 1 , query(0,4) : " ); Console.Write(query(version[1], 0, n - 1, 0, 4)); Console.Write( "In version 2 , query(3,4) : " ); Console.Write(query(version[2], 0, n - 1, 3, 4)); Console.Write( "In version 0 , query(0,3) : " ); Console.Write(query(version[0], 0, n - 1, 0, 3)); } } // This code is contributed by sanjeev2552 |
Javascript
<script> // JavaScript program to implement persistent // segment tree. class node { // Node constructor for l,r,v constructor(l, r, v) { this .left = l; this .right = r; this .val = v; } } // Declaring maximum number var MAXN = 100; // Making Node for tree // Input array var arr = Array(MAXN); // Root pointers for all versions var version = Array(MAXN); // Constructs Version-0 // Time Complexity : O(nlogn) function build(n, low, high) { if (low == high) { n.val = arr[low]; return ; } var mid = parseInt((low + high) / 2); n.left = new node( null , null , 0); n.right = new node( null , null , 0); build(n.left, low, mid); build(n.right, mid + 1, high); n.val = n.left.val + n.right.val; } /* Upgrades to new Version * @param prev : points to node of previous version * @param cur : points to node of current version * Time Complexity : O(logn) * Space Complexity : O(logn) */ function upgrade(prev, cur, low, high, idx, value) { if (idx > high || idx < low || low > high) return ; if (low == high) { // Modification in new version cur.val = value; return ; } var mid = parseInt((low + high) / 2); if (idx <= mid) { // Link to right child of previous version cur.right = prev.right; // Create new node in current version cur.left = new node( null , null , 0); upgrade(prev.left, cur.left, low, mid, idx, value); } else { // Link to left child of previous version cur.left = prev.left; // Create new node for current version cur.right = new node( null , null , 0); upgrade(prev.right, cur.right, mid + 1, high, idx, value); } // Calculating data for current version // by combining previous version and current // modification cur.val = cur.left.val + cur.right.val; } function query(n, low, high, l, r) { if (l > high || r < low || low > high) return 0; if (l <= low && high <= r) return n.val; var mid = parseInt((low + high) / 2); var p1 = query(n.left, low, mid, l, r); var p2 = query(n.right, mid + 1, high, l, r); return p1 + p2; } // Driver code var A = [1, 2, 3, 4, 5]; var n = A.length; for ( var i = 0; i < n; i++) arr[i] = A[i]; // Creating Version-0 var root = new node( null , null , 0); build(root, 0, n - 1); // Storing root node for version-0 version[0] = root; // Upgrading to version-1 version[1] = new node( null , null , 0); upgrade(version[0], version[1], 0, n - 1, 4, 1); // Upgrading to version-2 version[2] = new node( null , null , 0); upgrade(version[1], version[2], 0, n - 1, 2, 10); // For print document.write( "In version 1 , query(0,4) : " ); document.write(query(version[1], 0, n - 1, 0, 4)); document.write( "<br>In version 2 , query(3,4) : " ); document.write(query(version[2], 0, n - 1, 3, 4)); document.write( "<br>In version 0 , query(0,3) : " ); document.write(query(version[0], 0, n - 1, 0, 3)); </script> |
输出:
In version 1 , query(0,4) : 11In version 2 , query(3,4) : 5In version 0 , query(0,3) : 10
注:上述问题也可以通过脱机处理查询来解决,方法是根据版本对查询进行排序,并在相应的更新之后立即回答查询。
时间复杂性: 时间复杂度将与段树中的查询和点更新操作相同,因为我们可以考虑在O(1)中要完成的额外节点创建步骤。因此,新版本创建和范围和查询的每个查询的总体时间复杂度将为 O(对数n) .
本文由 尼蒂什·库马尔 .如果你喜欢GeekSforgek,并想贡献自己的力量,你也可以使用 写极客。组织 或者把你的文章寄去评论-team@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上,并帮助其他极客。 如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写下评论。


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



