持久数据结构

到目前为止，这里讨论的所有数据结构都是非持久性的（或临时的）。持久性数据结构是一种数据结构，在修改时始终保留其自身的早期版本。它们可以被认为是“不可变的”，就像更新一样 不到位 .

数据结构是 部分持久 如果可以访问所有版本，但只能修改最新版本。 完全持久 如果每个版本都可以访问和修改。合流持久性是指我们合并两个或多个版本以获得一个新版本。这会在版本图上产生一个DAG。

持久性可以通过简单的复制来实现，但这在CPU和RAM使用方面效率低下，因为大多数操作只会对DS进行一个小的更改。因此，更好的方法是利用新旧版本之间的相似性来共享它们之间的结构。

例如：

1. 链表连接： 考虑将n个和m个链表的两个单链表链结为它们的节点数。比如n>m。我们需要保留版本，也就是说，我们应该能够保留原始列表。 一种方法是复制每个节点并进行连接。O（n+m）用于遍历列表，O（1）用于添加（n+m–1）个连接。 另一种在时间和空间上更有效的方法是只遍历两个列表中的一个，并减少新连接。因为我们假设m

   

2. 二叉搜索树插入： 考虑在一个二叉搜索树中插入一个新节点的问题。作为一个二叉搜索树，新节点将被放置在一个特定的位置。从新节点到BST根节点的路径中的所有节点都将观察到结构的变化（级联）。例如，新节点是其子节点的节点现在将有一个新指针。这种结构上的变化会导致到根部的完整路径发生变化。考虑下面的树，其中每个节点中列出了节点的值。

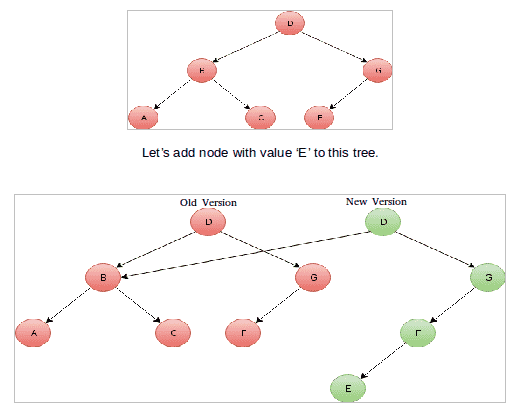
使数据结构持久化的方法 对于下面建议的方法，版本的更新和访问时间和空间随我们是实现完全持久化还是部分持久化而变化。

1. 路径复制： 制作一份我们将要更新的节点的副本。然后继续更新。最后，通过数据结构将更改级联回去，这与我们在上面的示例2中所做的非常相似。这会导致一系列更新，直到你到达一个没有其他节点指向的节点——根节点。 如何在时间t访问状态？维护一个按时间戳索引的根数组。
2. 脂肪结节： 顾名思义，我们让每个节点存储其修改历史，从而使其“胖”。
3. 带方框的节点： 摊销O（1）时间和空间可用于访问和更新。这种方法是由Sleator、Tarjan和他们的团队提出的。对于树，它涉及使用一个修改框，可以容纳： a、 对节点的一次修改（修改可能是对其中一个指针的修改，也可能是对节点的键或其他特定于节点的数据的修改） b、 应用mod的时间 时间戳对于到达我们关心的节点版本至关重要。你可以在这里了解更多。在这种算法中，给定任意时间t，在时间t的数据结构中最多存在一个修改框。因此，在时间t的修改将树拆分为三个部分：一个 部分包含时间t之前的数据，一部分包含时间t之后的数据，以及 一部分未受修改影响（来源： 麻省理工开放式课程 ). 非树型数据结构可能需要多个修改框，但仅限于摊销O（1）的节点度。

有用的链接：

1. 麻省理工开放式课程 （埃里克·德梅因）
2. 麻省理工开放式课程 （大卫·卡格）
3. 丹恩·托利弗的演讲
4. 维基页面

持久段树|集1（简介）

本文由 亚什·瓦里亚尼 。如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请发表评论