先决条件: 笛卡尔树
笛卡尔排序是一种自适应排序,因为如果数据被部分排序,它会更快地对数据进行排序。事实上,很少有排序算法利用这一事实。
例如,考虑数组{ 5, 10, 40,30, 28 }。输入数据也是部分排序的,因为“40”和“28”之间只有一次交换会产生完全排序的顺序。看看笛卡尔树排序将如何利用下面这个事实。
下面是用于排序的步骤。
第一步: 构建一个(最小堆) 笛卡尔树 从给定的输入序列。 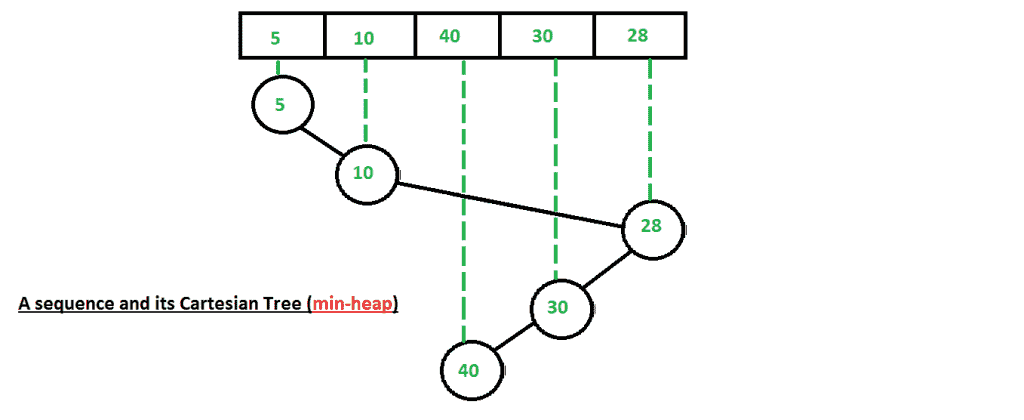
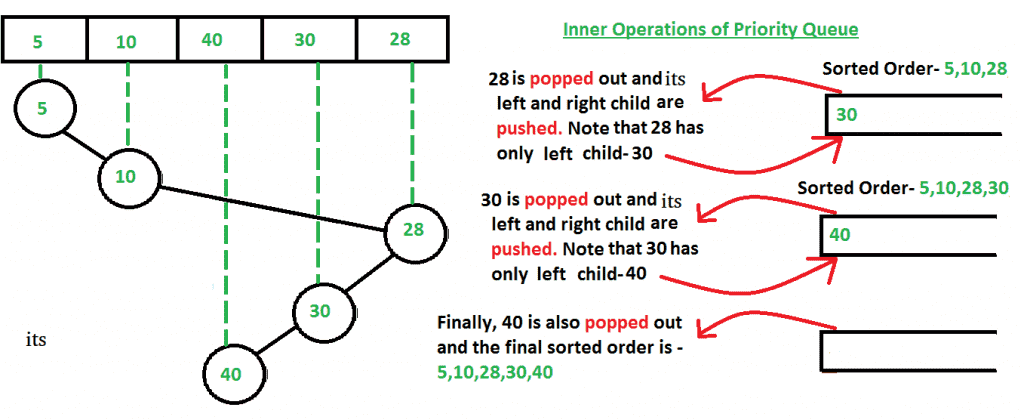
第二步: 从构建的笛卡尔树的根开始,我们将节点推送到优先级队列中。 然后我们将节点弹出到优先级队列的顶部,并以预排序的方式将弹出节点的子节点推送到优先级队列中。
- 将节点弹出到优先级队列的顶部,并将其添加到列表中。
- 首先按下弹出节点的左子节点(如果存在)。
- 按下弹出节点的右子节点(如果存在)。
如何构建(最小堆)笛卡尔树? 构建最小堆类似于构建(最大堆)笛卡尔树(在中讨论) 以前的职位 ),除了这样一个事实:现在我们从节点的父节点向上扫描到树的根节点,直到找到一个比当前节点的值小(并且不像最大堆笛卡尔树那样大)的节点,然后相应地重新配置链接以构建最小堆笛卡尔树。
为什么不只使用优先级队列? 有人可能会想,如果我们简单地在优先级队列中逐个插入输入数组的编号(即,不构建笛卡尔树),使用优先级队列无论如何都会导致排序数据。
但所花的时间却有很大不同。
假设我们使用输入数组{5,10,40,30,28}
如果我们只是一个接一个地插入输入数组编号(而不使用笛卡尔树),那么每次插入编号时,我们可能不得不浪费大量操作来调整队列顺序(就像插入新编号时典型的堆执行这些操作一样,因为优先级队列只是一个堆)。
然而,在这里我们可以看到,使用笛卡尔树只需要5次操作(参见上面两个图,我们在其中不断推动和弹出笛卡尔树的节点),这是线性的,因为输入数组中也有5个数字。所以我们看到笛卡尔树排序的最佳情况是O(n),堆排序需要更多的操作,因为它没有利用输入数据被部分排序的事实。
为什么要进行预序遍历? 答案是,由于笛卡尔树基本上是一个堆数据结构,因此遵循堆的所有属性。因此,根节点总是比它的两个子节点都小。因此,我们使用预排序方式弹出和推送,因为在优先级队列中,根节点总是比它的子节点更早推送,而且因为根节点总是小于它的两个子节点,所以我们不必在优先级队列中执行额外的操作。
// A C++ program to implement Cartesian Tree sort // Note that in this program we will build a min-heap // Cartesian Tree and not max-heap. #include<bits/stdc++.h> using namespace std; /* A binary tree node has data, pointer to left child and a pointer to right child */ struct Node { int data; Node *left, *right; }; // Creating a shortcut for int, Node* pair type typedef pair< int , Node*> iNPair; // This function sorts by pushing and popping the // Cartesian Tree nodes in a pre-order like fashion void pQBasedTraversal(Node* root) { // We will use a priority queue to sort the // partially-sorted data efficiently. // Unlike Heap, Cartesian tree makes use of // the fact that the data is partially sorted priority_queue <iNPair, vector<iNPair>, greater<iNPair>> pQueue; pQueue.push (make_pair (root->data,root)); // Resembles a pre-order traverse as first data // is printed then the left and then right child. while (! pQueue.empty()) { iNPair popped_pair = pQueue.top(); printf ( "%d " ,popped_pair.first); pQueue.pop(); if (popped_pair.second->left != NULL) pQueue.push (make_pair(popped_pair.second->left->data, popped_pair.second->left)); if (popped_pair.second->right != NULL) pQueue.push (make_pair(popped_pair.second->right->data, popped_pair.second->right)); } return ; } Node *buildCartesianTreeUtil( int root, int arr[], int parent[], int leftchild[], int rightchild[]) { if (root == -1) return NULL; Node *temp = new Node; temp->data = arr[root]; temp->left = buildCartesianTreeUtil(leftchild[root], arr, parent, leftchild, rightchild); temp->right = buildCartesianTreeUtil(rightchild[root], arr, parent, leftchild, rightchild); return temp ; } // A function to create the Cartesian Tree in O(N) time Node *buildCartesianTree( int arr[], int n) { // Arrays to hold the index of parent, left-child, // right-child of each number in the input array int parent[n],leftchild[n],rightchild[n]; // Initialize all array values as -1 memset (parent, -1, sizeof (parent)); memset (leftchild, -1, sizeof (leftchild)); memset (rightchild, -1, sizeof (rightchild)); // 'root' and 'last' stores the index of the root and the // last processed of the Cartesian Tree. // Initially we take root of the Cartesian Tree as the // first element of the input array. This can change // according to the algorithm int root = 0, last; // Starting from the second element of the input array // to the last on scan across the elements, adding them // one at a time. for ( int i=1; i<=n-1; i++) { last = i-1; rightchild[i] = -1; // Scan upward from the node's parent up to // the root of the tree until a node is found // whose value is smaller than the current one // This is the same as Step 2 mentioned in the // algorithm while (arr[last] >= arr[i] && last != root) last = parent[last]; // arr[i] is the smallest element yet; make it // new root if (arr[last] >= arr[i]) { parent[root] = i; leftchild[i] = root; root = i; } // Just insert it else if (rightchild[last] == -1) { rightchild[last] = i; parent[i] = last; leftchild[i] = -1; } // Reconfigure links else { parent[rightchild[last]] = i; leftchild[i] = rightchild[last]; rightchild[last]= i; parent[i] = last; } } // Since the root of the Cartesian Tree has no // parent, so we assign it -1 parent[root] = -1; return (buildCartesianTreeUtil (root, arr, parent, leftchild, rightchild)); } // Sorts an input array int printSortedArr( int arr[], int n) { // Build a cartesian tree Node *root = buildCartesianTree(arr, n); printf ( "The sorted array is-" ); // Do pr-order traversal and insert // in priority queue pQBasedTraversal(root); } /* Driver program to test above functions */ int main() { /* Given input array- {5,10,40,30,28}, it's corresponding unique Cartesian Tree is- 5 10 28 / 30 / 40 */ int arr[] = {5, 10, 40, 30, 28}; int n = sizeof (arr)/ sizeof (arr[0]); printSortedArr(arr, n); return (0); } |
输出:
The sorted array is- 5 10 28 30 40
时间复杂性: O(n) 最佳情况行为(输入数据部分排序时), O(n日志n) 最坏情况行为(输入数据未部分排序时)
辅助空间: 我们使用优先级队列和笛卡尔树数据结构。现在,在任何时刻,优先级队列的大小都不会超过输入数组的大小,因为我们一直在推送和弹出节点。因此我们使用O(n)辅助空间。
参考资料: https://en.wikipedia.org/wiki/Adaptive_sort http://11011110.livejournal.com/283412.html http://gradbot.blogspot.in/2010/06/cartesian-tree-sort.html http://www.keithschwarz.com/interesting/code/?dir=cartesian-树木分类 https://en.wikipedia.org/wiki/Cartesian_tree#Application_in_sorting
本文由 拉希特·贝尔瓦里亚 .如果你喜欢GeekSforgek,并且想贡献自己的力量,你也可以写一篇文章,并将文章邮寄到contribute@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上,并帮助其他极客。
如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写评论




![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



