笛卡尔树是由一组数据创建的树数据结构,这些数据遵循以下结构不变量:
- 树遵守最小(或最大)堆属性中的规则——每个节点都小于(或大于)其子节点。
- 按顺序遍历节点会产生与它们在初始序列中出现的顺序相同的值。
假设我们有一个输入数组-{5,10,40,30,28}。那么最大堆笛卡尔树就是。
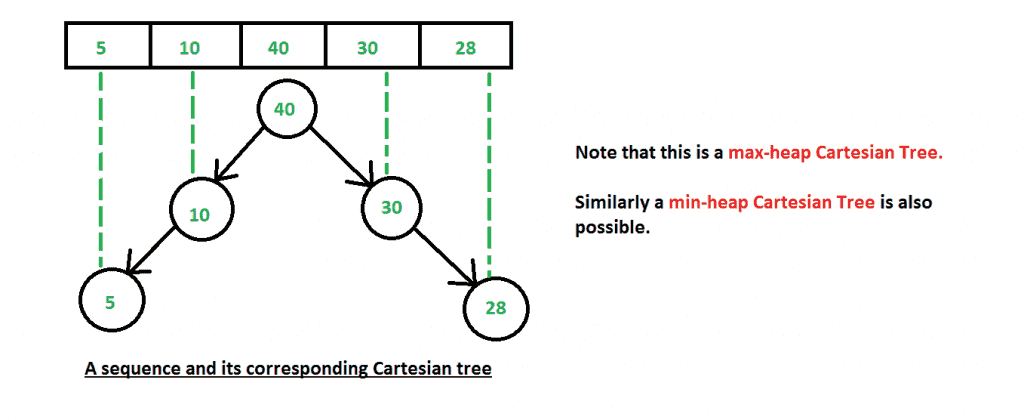
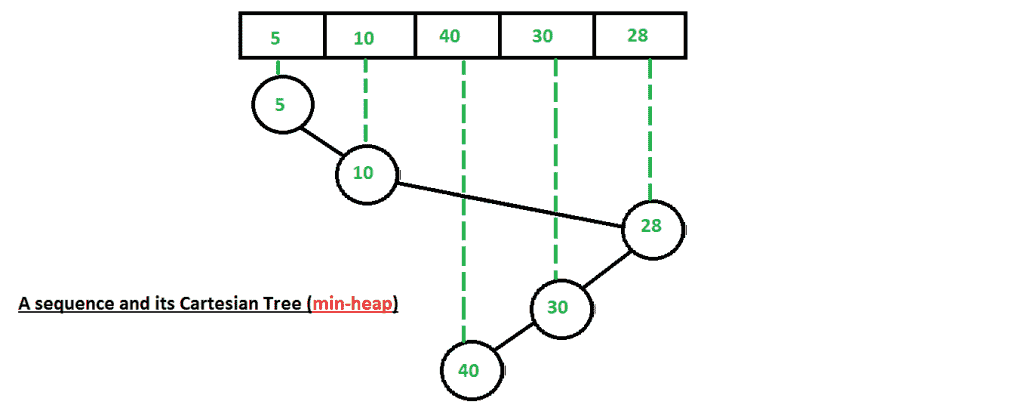
将创建上述输入数组的最小堆笛卡尔树-
注:
- 笛卡尔树不是高度平衡树。
- 不同数字序列的笛卡尔树总是唯一的。
不同数字序列的笛卡尔树总是唯一的。 我们将用归纳法证明这一点。作为基本情况,空树总是唯一的。对于归纳的情况,假设对于包含n’
- 将节点定位为最右侧节点的右子节点。
- 从节点的父节点向上扫描到树的根节点,直到找到一个值大于当前值的节点。
- 如果找到这样的节点,请将其右子节点设置为新节点,并将新节点的左子节点设置为上一个右子节点。
- 如果没有找到这样的节点,则将新子节点设置为根节点,并将新节点的左子节点设置为上一棵树。
CPP
// A O(n) C++ program to construct cartesian tree // from a given array #include<bits/stdc++.h> /* A binary tree node has data, pointer to left child and a pointer to right child */ struct Node { int data; Node *left, *right; }; /* This function is here just to test buildTree() */ void printInorder (Node* node) { if (node == NULL) return ; printInorder (node->left); cout << node->data << " " ; printInorder (node->right); } // Recursively construct subtree under given root using // leftChild[] and rightchild Node * buildCartesianTreeUtil ( int root, int arr[], int parent[], int leftchild[], int rightchild[]) { if (root == -1) return NULL; // Create a new node with root's data Node *temp = new Node; temp->data = arr[root] ; // Recursively construct left and right subtrees temp->left = buildCartesianTreeUtil( leftchild[root], arr, parent, leftchild, rightchild ); temp->right = buildCartesianTreeUtil( rightchild[root], arr, parent, leftchild, rightchild ); return temp ; } // A function to create the Cartesian Tree in O(N) time Node * buildCartesianTree ( int arr[], int n) { // Arrays to hold the index of parent, left-child, // right-child of each number in the input array int parent[n],leftchild[n],rightchild[n]; // Initialize all array values as -1 memset (parent, -1, sizeof (parent)); memset (leftchild, -1, sizeof (leftchild)); memset (rightchild, -1, sizeof (rightchild)); // 'root' and 'last' stores the index of the root and the // last processed of the Cartesian Tree. // Initially we take root of the Cartesian Tree as the // first element of the input array. This can change // according to the algorithm int root = 0, last; // Starting from the second element of the input array // to the last on scan across the elements, adding them // one at a time. for ( int i=1; i<=n-1; i++) { last = i-1; rightchild[i] = -1; // Scan upward from the node's parent up to // the root of the tree until a node is found // whose value is greater than the current one // This is the same as Step 2 mentioned in the // algorithm while (arr[last] <= arr[i] && last != root) last = parent[last]; // arr[i] is the largest element yet; make it // new root if (arr[last] <= arr[i]) { parent[root] = i; leftchild[i] = root; root = i; } // Just insert it else if (rightchild[last] == -1) { rightchild[last] = i; parent[i] = last; leftchild[i] = -1; } // Reconfigure links else { parent[rightchild[last]] = i; leftchild[i] = rightchild[last]; rightchild[last] = i; parent[i] = last; } } // Since the root of the Cartesian Tree has no // parent, so we assign it -1 parent[root] = -1; return (buildCartesianTreeUtil (root, arr, parent, leftchild, rightchild)); } /* Driver program to test above functions */ int main() { /* Assume that inorder traversal of following tree is given 40 / 10 30 / 5 28 */ int arr[] = {5, 10, 40, 30, 28}; int n = sizeof (arr)/ sizeof (arr[0]); Node *root = buildCartesianTree(arr, n); /* Let us test the built tree by printing Inorder traversal */ printf ( "Inorder traversal of the constructed tree : " ); printInorder(root); return (0); } |
JAVA
// A O(n) Java program to construct cartesian tree // from a given array /* A binary tree node has data, pointer to left child and a pointer to right child */ class GFG { static class Node { int data; Node left, right; }; /* This function is here just to test buildTree() */ static void printInorder (Node node) { if (node == null ) return ; printInorder (node.left); System.out.print(node.data + " " ); printInorder (node.right); } // Recursively construct subtree under given root using // leftChild[] and rightchild static Node buildCartesianTreeUtil ( int root, int arr[], int parent[], int leftchild[], int rightchild[]) { if (root == - 1 ) return null ; // Create a new node with root's data Node temp = new Node(); temp.data = arr[root] ; // Recursively construct left and right subtrees temp.left = buildCartesianTreeUtil( leftchild[root], arr, parent, leftchild, rightchild ); temp.right = buildCartesianTreeUtil( rightchild[root], arr, parent, leftchild, rightchild ); return temp ; } // A function to create the Cartesian Tree in O(N) time static Node buildCartesianTree ( int arr[], int n) { // Arrays to hold the index of parent, left-child, // right-child of each number in the input array int []parent = new int [n]; int []leftchild = new int [n]; int []rightchild = new int [n]; // Initialize all array values as -1 memset(parent, - 1 ); memset(leftchild, - 1 ); memset(rightchild, - 1 ); // 'root' and 'last' stores the index of the root and the // last processed of the Cartesian Tree. // Initially we take root of the Cartesian Tree as the // first element of the input array. This can change // according to the algorithm int root = 0 , last; // Starting from the second element of the input array // to the last on scan across the elements, adding them // one at a time. for ( int i = 1 ; i <= n - 1 ; i++) { last = i - 1 ; rightchild[i] = - 1 ; // Scan upward from the node's parent up to // the root of the tree until a node is found // whose value is greater than the current one // This is the same as Step 2 mentioned in the // algorithm while (arr[last] <= arr[i] && last != root) last = parent[last]; // arr[i] is the largest element yet; make it // new root if (arr[last] <= arr[i]) { parent[root] = i; leftchild[i] = root; root = i; } // Just insert it else if (rightchild[last] == - 1 ) { rightchild[last] = i; parent[i] = last; leftchild[i] = - 1 ; } // Reconfigure links else { parent[rightchild[last]] = i; leftchild[i] = rightchild[last]; rightchild[last] = i; parent[i] = last; } } // Since the root of the Cartesian Tree has no // parent, so we assign it -1 parent[root] = - 1 ; return (buildCartesianTreeUtil (root, arr, parent, leftchild, rightchild)); } static void memset( int [] arr, int value) { for ( int i = 0 ; i < arr.length; i++) { arr[i] = value; } } /* Driver code */ public static void main(String[] args) { /* Assume that inorder traversal of following tree is given 40 / 10 30 / 5 28 */ int arr[] = { 5 , 10 , 40 , 30 , 28 }; int n = arr.length; Node root = buildCartesianTree(arr, n); /* Let us test the built tree by printing Inorder traversal */ System.out.printf( "Inorder traversal of the" + " constructed tree : " ); printInorder(root); } } // This code is contributed by PrinciRaj1992 |
C#
// A O(n) C# program to construct cartesian tree // from a given array /* A binary tree node has data, pointer to left child and a pointer to right child */ using System; class GFG { class Node { public int data; public Node left, right; }; /* This function is here just to test buildTree() */ static void printInorder (Node node) { if (node == null ) return ; printInorder (node.left); Console.Write(node.data + " " ); printInorder (node.right); } // Recursively construct subtree under given root using // leftChild[] and rightchild static Node buildCartesianTreeUtil ( int root, int []arr, int []parent, int []leftchild, int []rightchild) { if (root == -1) return null ; // Create a new node with root's data Node temp = new Node(); temp.data = arr[root] ; // Recursively construct left and right subtrees temp.left = buildCartesianTreeUtil( leftchild[root], arr, parent, leftchild, rightchild ); temp.right = buildCartesianTreeUtil( rightchild[root], arr, parent, leftchild, rightchild ); return temp ; } // A function to create the Cartesian Tree in O(N) time static Node buildCartesianTree ( int []arr, int n) { // Arrays to hold the index of parent, left-child, // right-child of each number in the input array int []parent = new int [n]; int []leftchild = new int [n]; int []rightchild = new int [n]; // Initialize all array values as -1 memset(parent, -1); memset(leftchild, -1); memset(rightchild, -1); // 'root' and 'last' stores the index of the root and the // last processed of the Cartesian Tree. // Initially we take root of the Cartesian Tree as the // first element of the input array. This can change // according to the algorithm int root = 0, last; // Starting from the second element of the input array // to the last on scan across the elements, adding them // one at a time. for ( int i = 1; i <= n - 1; i++) { last = i - 1; rightchild[i] = -1; // Scan upward from the node's parent up to // the root of the tree until a node is found // whose value is greater than the current one // This is the same as Step 2 mentioned in the // algorithm while (arr[last] <= arr[i] && last != root) last = parent[last]; // arr[i] is the largest element yet; make it // new root if (arr[last] <= arr[i]) { parent[root] = i; leftchild[i] = root; root = i; } // Just insert it else if (rightchild[last] == -1) { rightchild[last] = i; parent[i] = last; leftchild[i] = -1; } // Reconfigure links else { parent[rightchild[last]] = i; leftchild[i] = rightchild[last]; rightchild[last] = i; parent[i] = last; } } // Since the root of the Cartesian Tree has no // parent, so we assign it -1 parent[root] = -1; return (buildCartesianTreeUtil (root, arr, parent, leftchild, rightchild)); } static void memset( int [] arr, int value) { for ( int i = 0; i < arr.Length; i++) { arr[i] = value; } } /* Driver code */ public static void Main(String[] args) { /* Assume that inorder traversal of following tree is given 40 / 10 30 / 5 28 */ int []arr = {5, 10, 40, 30, 28}; int n = arr.Length; Node root = buildCartesianTree(arr, n); /* Let us test the built tree by printing Inorder traversal */ Console.Write( "Inorder traversal of the" + " constructed tree : " ); printInorder(root); } } // This code is contributed by 29AjayKumar |
Javascript
<script> // A O(n) Javascript program to construct cartesian tree // from a given array /* A binary tree node has data, pointer to left child and a pointer to right child */ class Node { constructor(data) { this .data=data; this .left= this .right= null ; } } /* This function is here just to test buildTree() */ function printInorder (node) { if (node == null ) return ; printInorder (node.left); document.write(node.data + " " ); printInorder (node.right); } // Recursively construct subtree under given root using // leftChild[] and rightchild function buildCartesianTreeUtil(root,arr,parent,leftchild,rightchild) { if (root == -1) return null ; // Create a new node with root's data let temp = new Node(); temp.data = arr[root] ; // Recursively construct left and right subtrees temp.left = buildCartesianTreeUtil( leftchild[root], arr, parent, leftchild, rightchild ); temp.right = buildCartesianTreeUtil( rightchild[root], arr, parent, leftchild, rightchild ); return temp ; } // A function to create the Cartesian Tree in O(N) time function buildCartesianTree (arr,n) { // Arrays to hold the index of parent, left-child, // right-child of each number in the input array let parent = new Array(n); let leftchild = new Array(n); let rightchild = new Array(n); // Initialize all array values as -1 memset(parent, -1); memset(leftchild, -1); memset(rightchild, -1); // 'root' and 'last' stores the index of the root and the // last processed of the Cartesian Tree. // Initially we take root of the Cartesian Tree as the // first element of the input array. This can change // according to the algorithm let root = 0, last; // Starting from the second element of the input array // to the last on scan across the elements, adding them // one at a time. for (let i = 1; i <= n - 1; i++) { last = i - 1; rightchild[i] = -1; // Scan upward from the node's parent up to // the root of the tree until a node is found // whose value is greater than the current one // This is the same as Step 2 mentioned in the // algorithm while (arr[last] <= arr[i] && last != root) last = parent[last]; // arr[i] is the largest element yet; make it // new root if (arr[last] <= arr[i]) { parent[root] = i; leftchild[i] = root; root = i; } // Just insert it else if (rightchild[last] == -1) { rightchild[last] = i; parent[i] = last; leftchild[i] = -1; } // Reconfigure links else { parent[rightchild[last]] = i; leftchild[i] = rightchild[last]; rightchild[last] = i; parent[i] = last; } } // Since the root of the Cartesian Tree has no // parent, so we assign it -1 parent[root] = -1; return (buildCartesianTreeUtil (root, arr, parent, leftchild, rightchild)); } function memset(arr,value) { for (let i = 0; i < arr.length; i++) { arr[i] = value; } } /* Driver code */ /* Assume that inorder traversal of following tree is given 40 / 10 30 / 5 28 */ let arr = [5, 10, 40, 30, 28]; let n = arr.length; let root = buildCartesianTree(arr, n); /* Let us test the built tree by printing Inorder traversal */ document.write( "Inorder traversal of the" + " constructed tree : <br>" ); printInorder(root); // This code is contributed by rag2127 </script> |
输出:
Inorder traversal of the constructed tree :5 10 40 30 28
时间复杂性: 乍一看,代码似乎是O(n) 2. )buildCartesianTree()中有两个循环。但实际上,排序前序遍历平均需要O(NlogN)时间和O(n^2)时间。 辅助空间: 我们为每个节点以及三个额外的数组(leftchild[],rightchild[],parent[])声明一个结构,以保存输入数组中每个值的leftchild,rightchild,parent的索引。因此总O(4*n)= O(n) 额外的空间。 笛卡尔树的应用
- 笛卡尔树排序
- 序列上的最小范围查询相当于序列笛卡尔树上的最小公共祖先查询。因此,可以使用序列的笛卡尔树将RMQ简化为LCA。
- Treap,一种平衡的二叉搜索树结构 ,是(键、优先级)对的笛卡尔树;它根据优先级值进行堆排序,按顺序遍历会按排序顺序给出密钥。
- 后缀树 字符串的长度可以由后缀数组和最长的公共前缀数组构成。第一步是计算最长公共前缀数组的笛卡尔树。
参考资料: http://wcipeg.com/wiki/Cartesian_tree 本文由 拉希特·贝尔瓦里亚 .如果你喜欢GeekSforgek,并想贡献自己的力量,你也可以写一篇文章,然后将文章邮寄给评论-team@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上,并帮助其他极客。 如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写评论


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



