Treap（随机二叉搜索树）

喜欢 红黑 和 AVL Trees，Treap是一个平衡的二叉搜索树，但不能保证其高度为O（logn）。其思想是使用随机化和二进制堆属性以高概率保持平衡。搜索、插入和删除的预期时间复杂度为O（logn）。

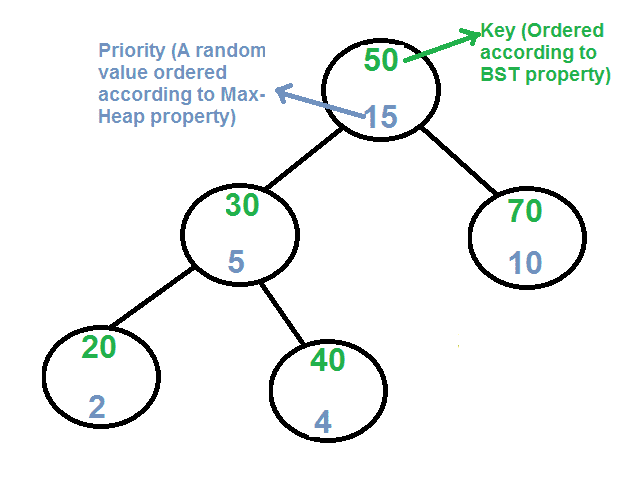
Treap的每个节点都维护两个值。 1) 钥匙 遵循标准BST顺序（左侧较小，右侧较大） 2) 优先事项 在最大堆属性之后随机分配的值。

Treap的基本操作： 与其他自平衡二进制搜索树一样，Treap在插入和删除期间使用旋转来维护最大堆属性。

T1, T2 and T3 are subtrees of the tree rooted with y (on left side) 
or x (on right side)           
                y                               x
               /      Right Rotation          /  
              x   T3   – – – – – – – >        T1   y 
             /        < - - - - - - -            / 
            T1  T2     Left Rotation            T2  T3
Keys in both of the above trees follow the following order 
      keys(T1) < key(x) < keys(T2) < key(y) < keys(T3)
So BST property is not violated anywhere. 

搜索（x） 执行标准 BST搜索 找到x。

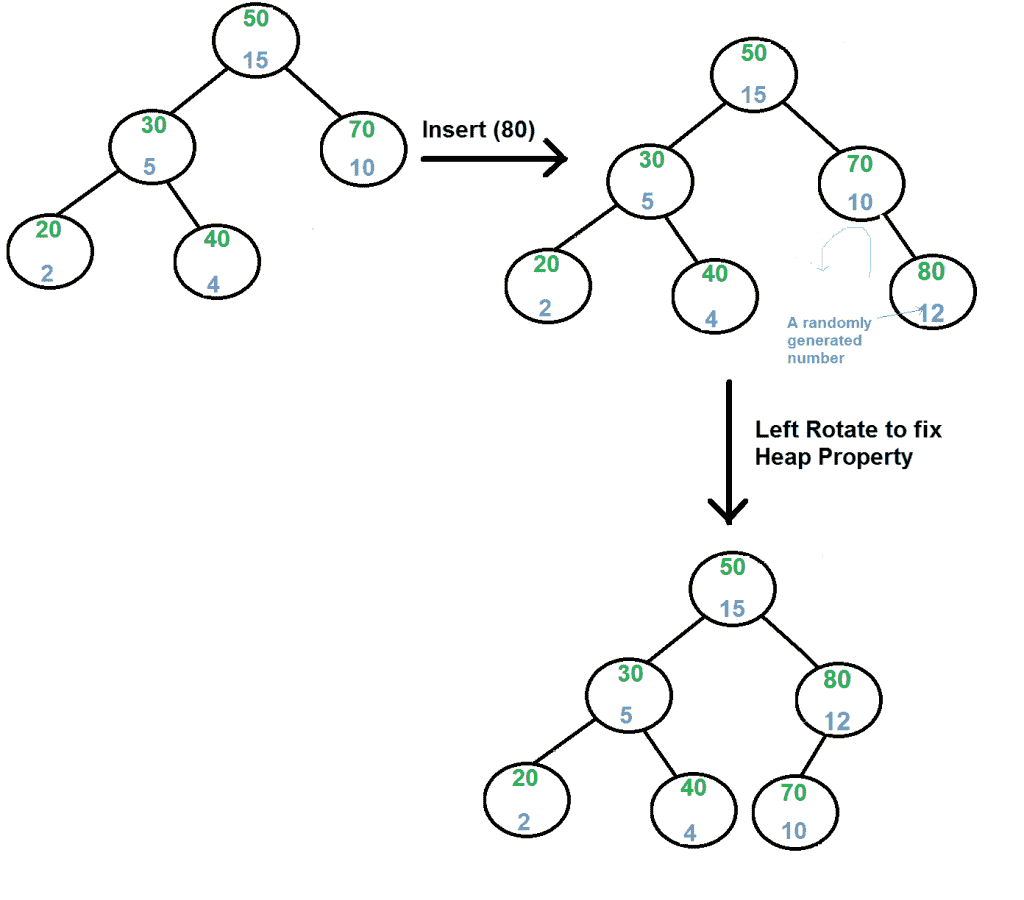
插入（x）： 1） 创建键等于x且值等于随机值的新节点。 2） 执行标准 BST插件 . 3） 使用旋转来确保插入节点的优先级遵循max heap属性。

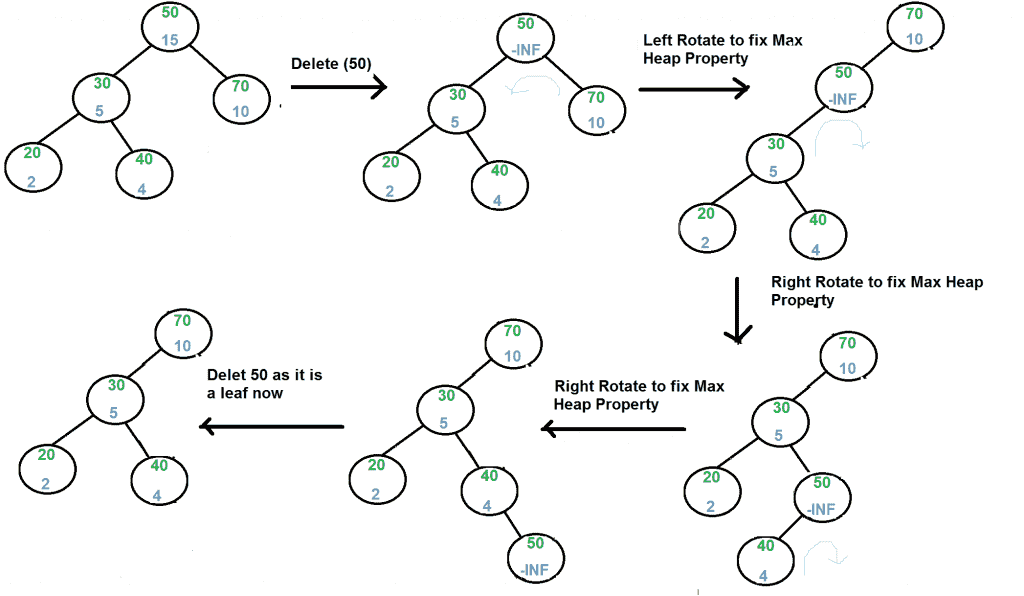
删除（x）： 1） 如果要删除的节点是叶，请将其删除。 2） 否则，用负无穷（-INF）替换节点的优先级，并进行适当的旋转，将节点向下移动到叶子。

参考 Treap搜索、插入和删除的实现 更多细节。

参考资料： https://en.wikipedia.org/wiki/Treap https://courses.cs.washington.edu/courses/cse326/00wi/handouts/lecture19/sld017.htm

如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请写下评论。