Dial算法（针对小范围权重的优化Dijkstra）-yiteyi-C++库

Dijkstra的最短路径算法用邻接列表表示法实现时，运行时间为O（Elog V）（参见 C.执行和基于STL的C++实现详细信息）。

null



Input : Source = 0, Maximum Weight W = 14
Output : 
     Vertex   Distance from Source
        0                0
        1                4
        2                12
        3                19
        4                21
        5                11
        6                9
        7                8
        8                14

如果最大权重很小（或边权重的范围很小），我们能否优化Dijkstra的最短路径算法，使其比O（E log V）更好地工作？ 例如，在上图中，最大重量为14。很多时候，中边上的权重范围都很小（即，所有边权重都可以映射到0、1、2..w，其中w是一个小数字）。在这种情况下，Dijkstra的算法可以通过使用不同的数据结构bucket进行修改，这就是Dijkstra算法的拨号实现。时间复杂性是 O（E+WV） 其中W是图的任何边上的最大权重，所以我们可以看到，如果W很小，那么这个实现比传统算法运行得快得多。以下是重要的观察结果。

任意两个节点之间的最大距离可以是max w（V–1）（w是最大边权重，两个顶点之间的边可以是max V-1）。
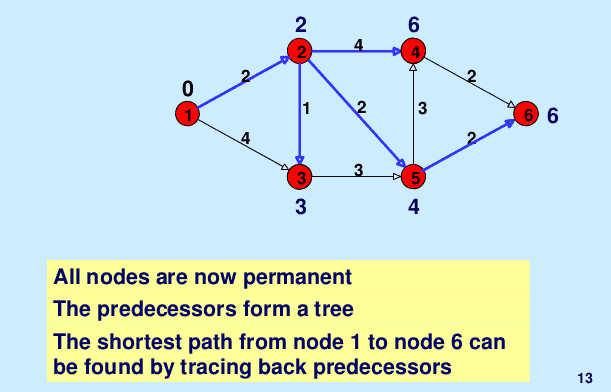
在Dijkstra算法中，距离以非递减的方式确定，也就是说，距离较近（到给定源）的顶点的距离在距离较远的顶点之前确定。

算法

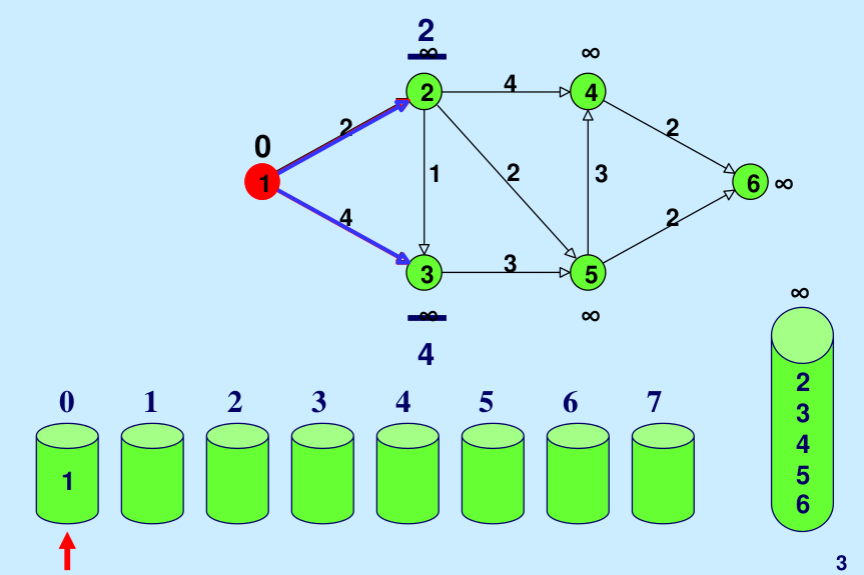
维护一些桶，编号为0，1，2，…，wV。
Bucket k包含距离等于k的所有临时标记的节点。
每个桶中的节点由顶点列表表示。
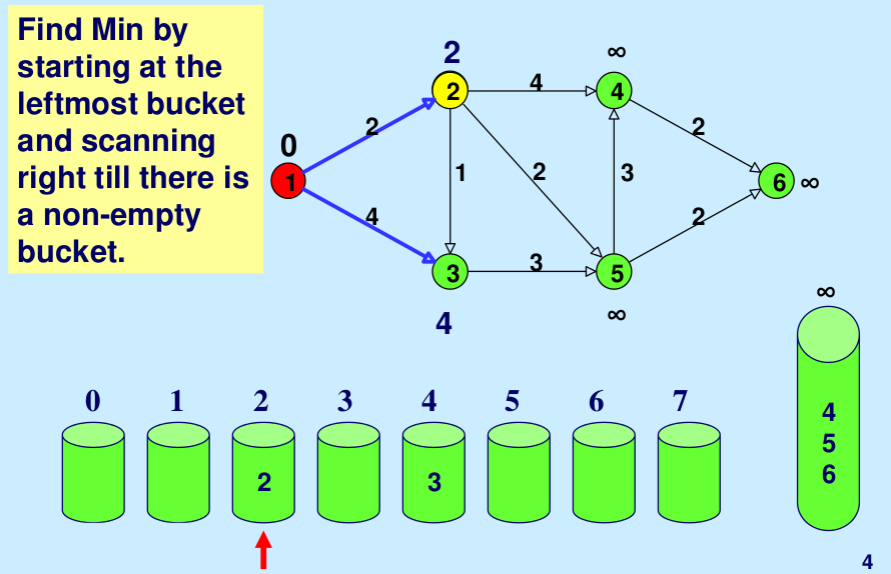
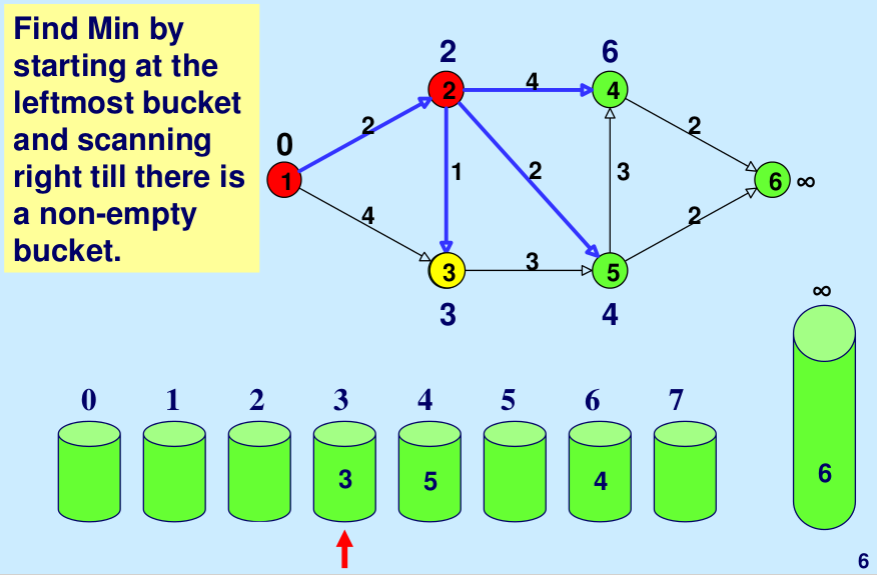
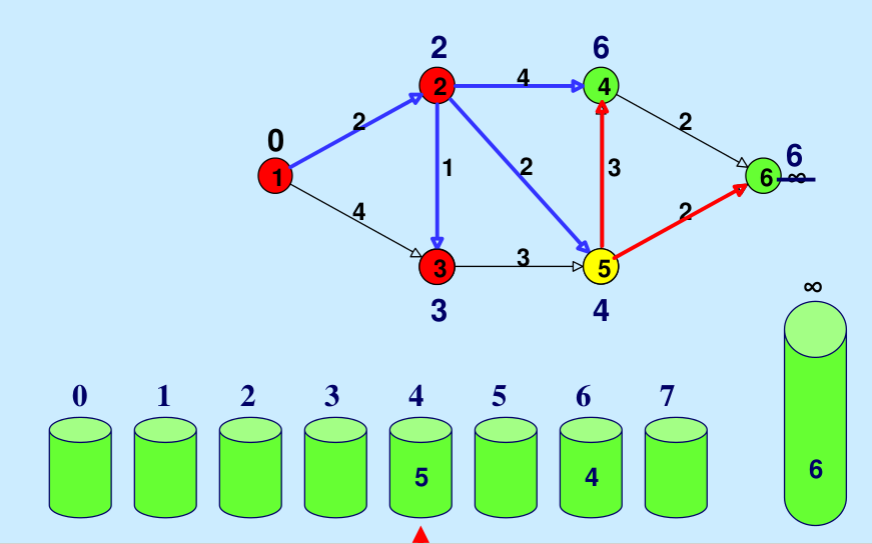
桶0，1，2，。。连续检查wV，直到找到第一个非空桶。根据定义，第一个非空桶中包含的每个节点都有最小距离标签。
在扫描过程中，这些带有最小距离标签的节点会一个接一个地被永久标记，并从存储桶中删除。
因此，涉及顶点的操作包括：
- 检查桶是否空
- 向桶中添加顶点
- 从桶中删除顶点。
当顶点的距离标签更改时，临时标记的顶点在桶中的位置将相应更新。
重复该过程，直到所有顶点都被永久标记（或所有顶点的距离最终确定）。

实施

由于最大距离可以是w（V–1），因此我们创建了wV bucket（更多是为了简化代码），用于实现算法，如果w很大，那么wV bucket可能会很大。

                     // C++ Program for Dijkstra's dial implementation                   
                     #include<bits/stdc++.h>                   
                     using                               namespace                               std;                   
                     # define INF 0x3f3f3f3f                   
                             
                     // This class represents a directed graph using                   
                     // adjacency list representation                   
                     class                               Graph                   
                     {                   
                                         int                               V;                               // No. of vertices                   
                             
                                         // In a weighted graph, we need to store vertex                   
                                         // and weight pair for every edge                   
                                         list< pair<                               int                               ,                               int                               > > *adj;                   
                             
                     public                               :                   
                                         Graph(                               int                               V);                               // Constructor                   
                             
                                         // function to add an edge to graph                   
                                         void                               addEdge(                               int                               u,                               int                               v,                               int                               w);                   
                             
                                         // prints shortest path from s                   
                                         void                               shortestPath(                               int                               s,                               int                               W);                   
                     };                   
                             
                     // Allocates memory for adjacency list                   
                     Graph::Graph(                               int                               V)                   
                     {                   
                                         this                               ->V = V;                   
                                         adj =                               new                               list< pair<                               int                               ,                               int                               > >[V];                   
                     }                   
                             
                     //  adds edge between u and v of weight w                   
                     void                               Graph::addEdge(                               int                               u,                               int                               v,                               int                               w)                   
                     {                   
                                         adj[u].push_back(make_pair(v, w));                   
                                         adj[v].push_back(make_pair(u, w));                   
                     }                   
                             
                     // Prints shortest paths from src to all other vertices.                   
                     // W is the maximum weight of an edge                   
                     void                               Graph::shortestPath(                               int                               src,                               int                               W)                   
                     {                   
                                         /* With each distance, iterator to that vertex in                   
                                         its bucket is stored so that vertex can be deleted                   
                                         in O(1) at time of updation. So                   
                                         dist[i].first = distance of ith vertex from src vertex                   
                                         dits[i].second = iterator to vertex i in bucket number */                   
                                         vector<pair<                               int                               , list<                               int                               >::iterator> > dist(V);                   
                             
                                         // Initialize all distances as infinite (INF)                   
                                         for                               (                               int                               i = 0; i < V; i++)                   
                                         dist[i].first = INF;                   
                             
                                         // Create buckets B[].                   
                                         // B[i] keep vertex of distance label i                   
                                         list<                               int                               > B[W * V + 1];                   
                             
                                         B[0].push_back(src);                   
                                         dist[src].first = 0;                   
                             
                                         //                   
                                         int                               idx = 0;                   
                                         while                               (1)                   
                                         {                   
                                         // Go sequentially through buckets till one non-empty                   
                                         // bucket is found                   
                                         while                               (B[idx].size() == 0 && idx < W*V)                   
                                         idx++;                   
                             
                                         // If all buckets are empty, we are done.                   
                                         if                               (idx == W * V)                   
                                         break                               ;                   
                             
                                         // Take top vertex from bucket and pop it                   
                                         int                               u = B[idx].front();                   
                                         B[idx].pop_front();                   
                             
                                         // Process all adjacents of extracted vertex 'u' and                   
                                         // update their distanced if required.                   
                                         for                               (                               auto                               i = adj[u].begin(); i != adj[u].end(); ++i)                   
                                         {                   
                                         int                               v = (*i).first;                   
                                         int                               weight = (*i).second;                   
                             
                                         int                               du = dist[u].first;                   
                                         int                               dv = dist[v].first;                   
                             
                                         // If there is shorted path to v through u.                   
                                         if                               (dv > du + weight)                   
                                         {                   
                                         // If dv is not INF then it must be in B[dv]                   
                                         // bucket, so erase its entry using iterator                   
                                         // in O(1)                   
                                         if                               (dv != INF)                   
                                         B[dv].erase(dist[v].second);                   
                             
                                         //  updating the distance                   
                                         dist[v].first = du + weight;                   
                                         dv = dist[v].first;                   
                             
                                         // pushing vertex v into updated distance's bucket                   
                                         B[dv].push_front(v);                   
                             
                                         // storing updated iterator in dist[v].second                   
                                         dist[v].second = B[dv].begin();                   
                                         }                   
                                         }                   
                                         }                   
                             
                                         // Print shortest distances stored in dist[]                   
                                         printf                               (                               "Vertex   Distance from Source"                               );                   
                                         for                               (                               int                               i = 0; i < V; ++i)                   
                                         printf                               (                               "%d     %d"                               , i, dist[i].first);                   
                     }                   
                             
                     // Driver program to test methods of graph class                   
                     int                               main()                   
                     {                   
                                         // create the graph given in above fugure                   
                                         int                               V = 9;                   
                                         Graph g(V);                   
                             
                                         //  making above shown graph                   
                                         g.addEdge(0, 1, 4);                   
                                         g.addEdge(0, 7, 8);                   
                                         g.addEdge(1, 2, 8);                   
                                         g.addEdge(1, 7, 11);                   
                                         g.addEdge(2, 3, 7);                   
                                         g.addEdge(2, 8, 2);                   
                                         g.addEdge(2, 5, 4);                   
                                         g.addEdge(3, 4, 9);                   
                                         g.addEdge(3, 5, 14);                   
                                         g.addEdge(4, 5, 10);                   
                                         g.addEdge(5, 6, 2);                   
                                         g.addEdge(6, 7, 1);                   
                                         g.addEdge(6, 8, 6);                   
                                         g.addEdge(7, 8, 7);                   
                             
                                         //  maximum weighted edge - 14                   
                                         g.shortestPath(0, 14);                   
                             
                                         return                               0;                   
                     }                   

输出：

Vertex Distance from Source
0     0
1     4
2     12
3     19
4     21
5     11
6     9
7     8
8     14

插图在这里

本文由Utkarsh Trivedi撰稿。如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请写下评论。

文章版权归作者所有，未经允许请勿转载。

THE END

技术文章